CT系统参数标定及成像

王 琪

（江西财经大学经济学院， 江西 南昌 330000）

1 问题重述

CT（Computed Tomography），即计算机断层扫描，利用样品对射线能量的吸收特性对样品进行断层成像，由此获取样品内部的结构信息。平行入射的X射线垂直于探测器平面，每个探测器单元看成一个接收点，且等距排列。X射线的发射器和探测器相对固定不变，整个发射—接收系统绕某旋转中心逆时针旋转180次。对于每一个X射线方向，在探测器上测量经位置固定不动的二维待检测介质吸收衰减后的射线能量，并经过增益等处理后得到180组接收信息。为减小误差，需要对安装好的CT系统进行参数标定，并据此对未知结构的样品进行成像[1-2]。

问题1：在正方形托盘上放置两个均匀固体介质组成的标定模板，模板的几何信息如图1所示，其中每点的数值反映该点的吸收强度，即“吸收率”。要求根据模板及其接收信息，确定CT系统旋转中心在正方形托盘中的位置、探测器单元之间的距离以及该CT系统使用的X射线的180个方向。

问题2：给出利用上述CT系统得到的某未知介质的接收信息。利用问题1中得到的标定参数，确定该未知介质在正方形托盘中的位置、几何形状和吸收率等信息。另外，给出图2所给的10个位置处的吸收率。

2 模型假设

1）假设将每个探测器视为一个接收点，其自身的宽度忽略不计。

2）假设X射线垂直于椭圆短轴透射样品时在探测器上得到的投影数据最大。

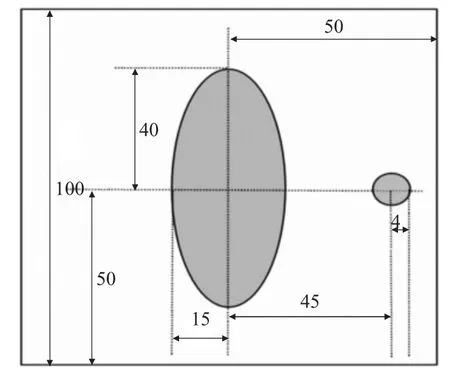
图1 模板示意图（mm）

图2 10个位置示意图（mm）

3）假设X射线垂直于椭圆长轴透射样品时在探测器上得到的投影面积最大。

3 给定模板下的CT系统参数设定模型

3.1 探测器单元之间的距离

本文假设每个探测器单元看成一个接收点，且512个探测器等距排列。设所给模板中的圆形介质直径为d，接收到经过圆形介质的X射线的探测器个数为k，探测器单元之间的距离为l，则有：

根据180个不同方向上，512个探测器对模板的接收信息，选取第1个方向的数据为例，做出不同探测器得到的吸收率的图像。易知，图像第一段波动曲线即为X射线经过椭圆形介质得出的吸收率，第二段波动曲线即为X射线经过圆形介质得出的吸收率。由此，接收到经过圆形介质的X射线的探测器个数即为第二段波动曲线在轴上的截距。由计算可读取得出，接收到经过圆形介质的X射线的探测器为第402至第430个，共29个探测器。又由图1模板示意图可知，圆形介质的直径为8 mm。因此，探测器单元之间距离为0.275 8 mm.

3.2 CT系统旋转中心在托盘中的位置

3.2.1 对于旋转中心在托盘中心附近的证明

观察所给每列数据，存在两种情况：只有一个连续的正数群，被0值隔开的两个连续的正数群，可知无论是分开还是聚合的正数群，在最中间第256和第257个探测器处的数值M附近存在距离ε个探测器数据L，有：

令椭圆中心与旋转中心距离为d'，已知探测器间距d，有：

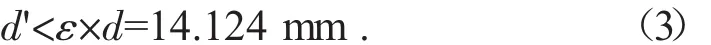
由此可得，旋转中心位于正方形托盘中心的附近。

3.2.2 旋转中心在托盘中的位置模型

以椭圆介质中心为原点建立平面直角坐标系，水平于正方形托盘的方向为x轴且向右为正方向，垂直方向为y轴且向上为正方向。为方便计算，本文选取X射线分别垂直于x轴与y轴的两种情况，分别计算旋转中心的横坐标与纵坐标。

当X射线垂直于y轴，即探测器旋转于坐标系左侧时，此时可根据计算误差值得出旋转中心纵坐标。由所给数据可得非零数值最多的一列，记为Cmax，表示在该方向上读取到经过介质的X射线的探测器数量最多。设该列上最左端探测器和最右端探测器分别为第a个和第b个探测器。取两端探测器平均值，根据平均值所在位置与原点差异即可得出旋转中心纵坐标y0，即：

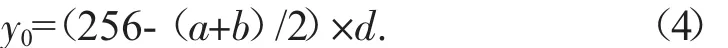
当X射线垂直于x轴，即探测器旋转于坐标系正上方时，此时可根据计算误差值得出旋转中心横坐标。由所给数据可得非零数值最少的一列，记为Cmin，表示在该方向上读取到经过介质的X射线的探测器数量最少。设该列上最左端探测器和最右端探测器分别为第e个和第f个探测器。取两端探测器平均值，根据平均值所在位置与原点差异即可得出旋转中心横坐标x0，即：

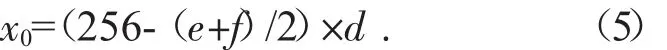
3.2.3 模型求解

用MATLAB编程，算法如下：首先，找出非零数值最多的一列Cmax及最少的一列Cmin；其次，分别找出以上两列的最左端探测器和最右端探测器；最后将数值代入式（4）（5）中求解。求得结果为Cmax=58，其最左端探测器和最右端探测器分别为第92个和第169个探测器；Cmin=150，其最左端探测器和最右端探测器分别为第276个和第380个探测器。旋转中心坐标为（-9.239 3，5.516 0）。

3.3 X射线的180个方向

对于X射线的180个方向，可依据特殊方向及每次的旋转角度得出。当X射线从椭圆介质的短轴方向射入时，对应数据中该列数据具有最高的对称性，用MATLAB编程搜索可得为第61列，可知第61个方向上不同探测器得到的吸收率。同理，当X射线从椭圆介质的长轴方向射入时，X射线穿过物体的厚度最大，物体对射线的吸收量最大，即吸收率最大。由所给数据可知吸收率最大的一列为第151列，可知第151个方向上不同探测器得到的吸收率。

从第61次旋转到第151次，旋转90°，则每次旋转角度为1°。又第61次旋转后X射线垂直y轴，由题意知从初始位置逆时针旋转至第61个方向，中间转过角度为61°。则初始入射位置与y轴夹角为29°。X射线180个方向结果见图3所示。

图3 X射线180个方向对应结果图

4 基于Radon变换重建的吸收率求解模型

4.1 X射线强度衰减与图像重建的原理

当X射线穿过均匀材料的介质时，根据Lambert Beers定理，射线强度按指数规律衰减，满足公式：

其中，I为穿过介质后射线的强度，I0为入射前的射线强度，μ为衰减系数，即介质对射线的吸收系数，x为介质的厚度。

当X射线穿过一个含有不同吸收系数材料的非均匀物体时，则有：

其中，μ（x，y）是沿L的线积分，即随路径L变化的衰减系数的函数。将函数μ（x，y）在平面上沿直线L的线积分定义为：

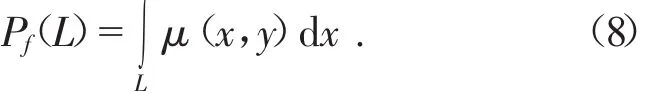
上式称为 μ（x，y）的 Radon 变换，μ（x，y）关于某直线的Radon变换就是μ（x，y）沿该直线的一维投影。Radon变换的逆变换则对应图像二维函数的重建。

4.2 未知介质的几何形状和吸收率

利用变换的逆变换，可编写程序得出问题2中所给数据的未知介质平面图，未知介质的几何形状为椭圆形，椭圆右侧有两个小椭圆形小洞。

用MATLAB可找出大椭圆形最左端、最右端、最上端及最下端的4个坐标点分别为（6.06,44.90），（87.6，49.86），（48.48，25.62），（47.38，69.42）。将题目所给10个位置处转化为椭圆形图中对应点的坐标，分别找出对应的10个吸收率，从左至右分别为0，0，0.485 1，0，0.497 7，0，0，0，0，0。