混凝土箱梁桥施工监控受温度变化影响及修正分析

邓 锐

(太原高速公路有限公司机械化养护中心,山西 太原 030000)

0 引言

混凝土箱梁结构凭借其优良的截面特性得到了广泛的应用。由于箱型截面面积大，各部位受太阳辐射不同使得箱型梁桥受太阳日照等因素下很容易形成箱梁内表面、外表面的温度差，竖向温度差值等表面温度差值，这个温度差值则会引起温度应力，一旦温度差值过大，引起的温度应力超过混凝土极限拉应力时则容易产生温度裂缝。混凝土箱梁施工过程中的温度场变化产生的影响力往往超过了混凝土结构参数误差影响，因此在进行混凝土箱梁施工参数识别中有必要充分考虑温度影响的程度，并结合现场施工进行温度影响的消除处理。一般通过进行温度影响的理论分析及现场试验控制来消除温度影响，这也成为了混凝土箱梁桥施工过程温度影响控制研究的热点之一[1,2]。颜东煌等基于某斜拉桥施工温度控制实例进行了消除温度影响的理论创新，提出了基于现场实测数据分析桥梁温度场的分段多项式函数法及控制消除温度影响的方法，运用结果表明了该方法的有效性[3]。

本文基于现有的箱梁结构温度控制及消除的现实理论基础，结合现场实测数据进行施工工况下的温度影响分析及修正，达到较好消除现场施工温度影响的目的。

1 工程概况

某桥梁中心桩号为K1+284，起点桩号为K0+510.26，终点桩号为K2+054.24，桥梁全长1 543.98 m。主桥上构采用82 m+2×140 m+82 m变截面预应力混凝土连续梁，主梁为单箱单室箱梁。箱梁采用挂篮悬臂浇筑，共3个“T”，全桥6套挂篮。箱梁节段划分：中跨划分为支架现浇段(0号段)和19个挂篮悬浇段(1号段～19号段)，边跨划分为2个支架现浇段(0号段及20号段)和19个挂篮悬浇段(1号段～19号段)。

箱梁顶横坡为2%的人字坡，箱梁顶宽1 620 cm，底宽800 cm，悬臂宽435 cm，底板厚度20 cm，中跨跨中及边跨梁端梁高380 cm，底板厚度32 cm，墩顶0号块顶板厚100 cm，其他梁段顶板厚30 cm。箱梁某横截面图如图1所示。

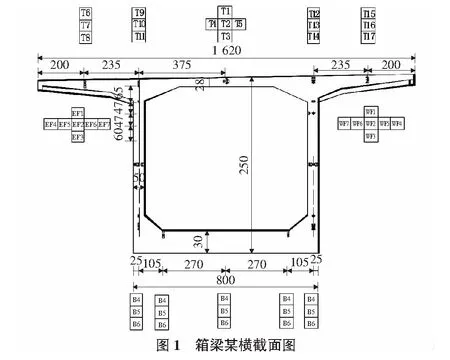
2 混凝土箱梁温度效应理论计算与现场实测应力

2.1 箱梁应力实测—应变测试仪器

实测采用长沙亿拓土木工程监测仪器有限公司生产的YT-ZX-0200系列应变测试仪器，该系列测试仪器可用于各种混凝土结构内部的应变测量，如各种混凝土桩、建筑、大坝、隧道及桥梁等的应变监测。

YT-ZX-0200系列的性能参数如表1所示。

表1 YT-ZX-0200系列埋入式混凝土应变计性能参数

2.2 箱梁截面温度梯度应力的选择

应变传感器埋设时将应变计按需测量方向轻绑在结构钢筋上(埋入式钢梁应变计固定在被测钢梁上)，然后灌入混凝土。

埋入式混凝土应变计根据张力弦原理制造，使用频率作为输出信号，抗干扰能力强，远距离输送产生的误差极小；并且内置温度传感器，对外界温度影响产生的变化进行温度修正；每个传感器内部有计算芯片，自动对测量数据进行换算而直接输出物理量，减少人工换算的失误和误差；全部元器件进行严格测试和老化筛选，尤其是高低温应力消除试验，增强弦的稳定性和可靠性[4]。

2.3 箱梁温度梯度计算应力与实测应力—应变的比较

研究对象主要为：0号块、边跨跨中及中跨跨中三个关键箱梁截面；通过测定三个关键截面在最不利温度梯度条件下的实测应力，并与三个关键截面的理论计算应力进行对比分析。

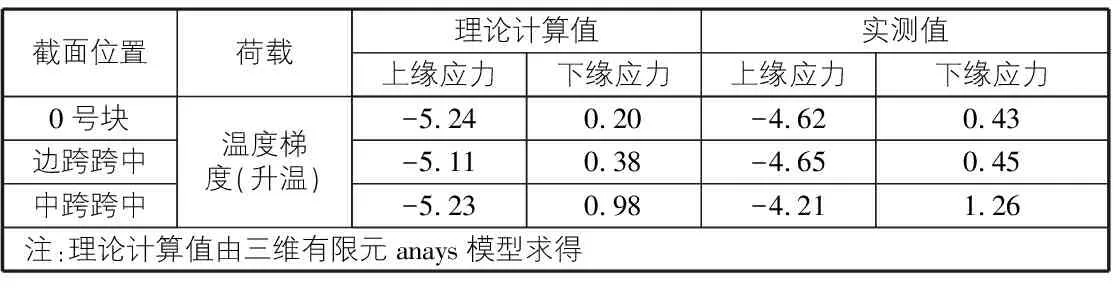
表2 不同箱梁截面在温度梯度作用下产生的应力值 N/mm2

由表2可知，三个关键截面的理论计算应力与实测应力的差异性较大，且差值高达1 MPa，通过对影响应力因素进行分析，发现引起差值明显的主要原因有：

1)通常一般截面的应力分布都服从虎克定律，箱梁属于薄壁结构存在剪力滞效应，然而在计算箱梁应力值时并未充分考虑到该效应，从而引起计算值和实测值的误差较大。

2)箱梁截面应力值的理论计算是以0 ℃为基础进行的，而现场实测时的基础温度不为0 ℃，尽管以温度补偿的方式对整体温度进行了修正，但实际上仍然存在一定误差。

3)箱梁截面应力值的理论计算时，认为构成箱梁混凝土结构的材料是均匀的，其弹性模量为常数，而实际上构成箱梁混凝土结构材料并非均匀，弹性模量具有很大的离散性。

3 温度变化对施工监控影响及修正分析

3.1 温度对施工监控影响危害

温度环境变化对箱梁结构体系的内力分布有一定影响，本项目采用悬臂施工，温度影响悬臂施工点如下：

1)主梁标高。

如在挂篮施工浇筑混凝土过程中，先对挂篮标高放样，绑扎钢筋，9 h后再进行混凝土浇筑，显然在初测挂篮标高与9 h后浇筑混凝土时挂篮标高存在差异性，这种差异性由温度造成，因此需要进行温度影响调整来减少温度变化对主梁线形影响。

2)挠度监测的准确度、可靠性。

温度变化导致主梁挠度增大，产生理论计算值与实际测量值的差异。

3)合龙。

温度影响箱梁结构内力，因此一般选择深夜或者凌晨温度较低时间段进行合龙，从而减少温度影响对合龙段混凝土质量影响。

4)应力监测准确性。

温度影响导致实测值与计算值不吻合，不利于应力分析。

3.2 消除温度影响的方法

1)固定实测法。

本项目中为了克服温度对长悬臂箱梁标高和挠度监测影响，对挂篮立模标高采用固定时间进行放样、挠度监测。在清晨5:00～7:00，进行挂篮立模标高的放样和箱梁挠度变形监测时，此时间段温度变化最小，温度的影响最小，可忽略不计。

2)相对标高法。

本项目中也采用相对标高法进行挂篮立模标高的放样，具体过程如下[5]：

设前后两节箱梁的梁底监控计算标高分别为H1和H2，这两节箱梁梁底的监控计算高差为Δh12。则有：

Δh12=H1-H2

(1)

若前一节箱梁是按监控计算的立模标高进行放样和施工，在某一时刻，欲放后一节箱梁的立模标高，设此时温度对前一块和后一块箱梁的标高影响量分别为ΔH1和ΔH2，而且此时实测的前一块箱梁的梁底标高为H11，则H11中含有此时温度对这一块箱梁标高的影响量ΔH1，即有:

H11=H1+ΔH1

(2)

后一节箱梁的梁底放样标高H22，则有：

H22=H1+Δh12-ΔH3

(3)

把式(1)和式(2)代入式(3)中，则有:

H22=H1+ΔH1+H2-H1-ΔH2=H2+ΔH1-ΔH2

(4)

若有：

ΔH1=ΔH2

(5)

则由式(4)可得：H22=H2，显然此时的H22已经不含温度对后一节箱梁标高的ΔH2。

本项目悬臂法施工中，不同箱梁段长度在5 m以下，可认为同一时刻下，ΔH1≈ΔH2,误差在2 mm左右，相对于挂篮立模标高，2 mm误差可忽略不计。

由以上分析可知，进行前块箱梁施工放样后，后一节箱梁立模标高可根据前一块箱梁梁底标高H11及Δh12按照式(3)计算得到，显然这个过程已经消除了温度变化对悬臂箱梁的影响，该过程即为相对标高法。

3)施工监控中的温度应力修正。

桥梁监控中需要对应力监测结果进行温度修正。本项目中测得的混凝土温度变化及应力变化分析见图2，图3。

混凝土的实际温度值难以在施工过程中检测准确，而一般采用修正后的环境温度作为混凝土内温度。本文运用应变元件进行混凝土温度的修正，应变元件能够实现对温度及应变的测量，修正后的值也较为准确。尤其是温度与应力存在一定的函数关系，应变元件数据可以充分挖掘这层函数关系，因而方便进行温度应力修正分析。

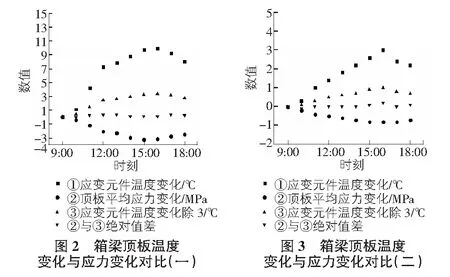
监测中发现，元件所处位置的混凝土温度每升高1 ℃，混凝土压应力就大约增加0.33 MPa，如表3所示，通过元件的温度变化量除以3，得到的数值与应力变化的绝对值之差较小。又取元件处的单位长度混凝土，温度升高1 ℃时，应变为1×10-5，弹性模量为3.6×104MPa，应力为0.36 MPa，与元件温度和应力关系相符。可见，通过对应变元件的应变与温度数值关系进行分析，可得到变化温度与应变的关系式，即：

σ=ΔT×a

(6)

其中，σ为应力；ΔT为变化温度绝对值；a为系数，这里取0.33。

以上获得了实测温度与应力之间的函数关系，为验证函数关系的准确性，这里对2号墩3号块预应力张拉完后的温度应力进行修正，见表3。

表3 2号墩3号块混凝土应力修正实例

可见，修正后的应力误差比修正前明显变小，与理论值更加接近，显然采用这种方法进行应力修正是合适的。

4 结语

1)三个关键截面的理论计算应力与实测应力的差异性较大，差值最高达1 MPa，因此不能忽略温度应力影响；

2)运用应变元件进行混凝土温度的修正，找出了温度与应力存在的函数关系，即混凝土温度每升高1 ℃，混凝土压应力就大约增加0.33 MPa，现场修正实例表明：温度影响修正前温度应力实测值与理论计算值存在较大差异，修正后的应力误差比修正前明显变小，与理论值更加接近，从而表明基于温度增加与应力增加关系进行应力修正是合适的。