球面渐开线弧齿锥齿轮参数化建模*

2018-10-09 06:37倪胜利邹艳龙李文凯

组合机床与自动化加工技术 2018年9期

倪胜利，陈霞，邹艳龙，刘芳，李文凯

(武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，武汉 430081)

0 引言

弧齿锥齿轮为一种局部点接触的不完全共轭的齿轮副，几何模型相当复杂，使用UG等三维建模软件却无法建立其精确的三维模型。对一些高端精密应用的弧齿锥齿轮，齿根过渡曲面对轮齿的强度和使用寿命有重要的影响。

李兆文等[1]利用展成法的原理，用VB编程获得弧齿锥齿轮的齿面点，借助于Pro/E软件建立弧齿锥齿轮实体模型。张武刚等[2]用切齿原理和实际切齿过程建立几何仿真模型。任燕[3]和杨宏斌[4]用展成法原理推导弧齿球面渐开线方程，结合MATLAB和SolidWorks软件建立了弧齿锥齿轮模型。Litvin[5]推导出刀具外侧方程和刀尖圆角方程及齿面展成原理，却没有给出齿根过渡曲面的推导过程。唐进元[6]运用啮合方程和切齿原理推导出弧齿锥齿轮工作齿面和过渡曲面方程，在MATLAB中计算出齿面的数据点，再导入到Pro/E中建立了含有过渡曲面的弧齿锥齿轮。刘光磊[7]根据齿轮加工的展成法，通过坐标转换顺序，从刀具方程得到了齿轮的齿面方程和齿根过渡曲面方程。以上所述主要是以近似球面渐开线齿形的设计与加工研究为主，而球面渐开线理论在弧齿锥齿轮设计中却起步比较晚。传统方式加工的齿轮难以获得理想的球面渐开线齿形，该齿轮传动体系属于局部点接触，它采用了一种近似球面渐开线的齿形，接近于共轭传动，造成了齿轮啮合不理想的现实问题。正因为如此，李丹红[8]用球面渐开线理论应用于建模中，借助CAD曲面设计功能为主进行建模，但其中没有设计到齿根过渡曲面的设计。

为了得到理想啮合的弧齿锥齿轮模型，本文基于球面渐开线理论，推导出弧齿锥齿轮的参数化方程，不仅给出了球面渐开线方程，还推导出了齿形方程，最后还给出了齿根过渡曲面方程。整个模型的设计都在MATLAB环境中实现，不存在数据丢失等问题。轮齿由端面、齿廓面、齿顶面和齿根面组成，齿廓面分成齿面、齿根圆锥面、齿根过渡曲面3部分，轮齿的齿面由球面渐开线和齿向曲线组成。轮齿端面分成6个子区域，每个区域通过球面渐开线、齿顶、齿根、齿根过渡等部分的网格数目协调地连接起来。

1 弧齿锥齿轮啮合原理

弧齿锥齿轮齿形理论上为球面渐开线，为便于制造，在实际生产中将弧齿锥齿轮大端齿形展成平面，把大端球面渐开线转化成平面渐开线，从而得到近似的齿形，精确的弧齿锥齿轮模型必须使用球面渐开线。

当平面在基圆锥上滚动时，平面上的一点运动轨迹称为球面渐开线。如图1所示，圆平面T与基圆锥OKoO1相切并在锥面上作纯滚动，圆平面上的动点K在空间的运动轨迹为渐开线。由于动点K在球面渐开线上任意位置到基圆锥顶点O的距离始终相等，故该渐开线是以O点为球心的球面上。当圆平面由初始OK位置滚动到ON位置时，动点K的轨迹为球面渐开线K0K。

图1 球面渐开线的形成原理

过点K作轴线OO1垂直的平面，交轴线OO1于Q点，交母线OK0于P点。在直角三角形OKQ、OKP、OPN中，存在如下关系：

(1)

通过渐开线的性质可知：

(2)

(3)

由上述方程可推导出：

(4)

由球面三角学和边角关系可得出：

(5)

球面渐开线上任意一点K的偏角可求出：

(6)

在图1中的球面坐标系中，可表示为：

(7)

式中，δk为球面渐开线上任意点所对应锥角，δb为基圆锥角。

在产形线K0Kt上分别取等分点Kn(n=0,1,...,t)，当大端面上的点Kn=0每次旋转θ角度，就完成一条球面渐开线曲线，线段OK0作为纯滚动时的切线就自动转过一定的角度θn，以下一点Kn=1再作空间球面渐开线运动形成一条球面渐开线曲线，循环上述操作，直到产形线起点K0指向末点Kt，则所有球面渐开线曲线构成了整个齿面，如图2所示。当球面半径R和旋转角度θ变化时，曲线K0Kt点Kn(n=0,1,...,t)所形成的曲线便可形成球面渐开线齿面。

图2 球面渐开线齿面形成原理图

2 弧齿锥齿轮齿面的基本组成

2.1 弧齿锥齿轮球面渐开线

如图3所示，节平面为产形面，所绘制的圆为齿宽的中点圆；O1为刀盘中心位置，刀盘半径是RD，O是锥顶，螺旋角为LXJ。

通过余弦定理可求得：

(8)

对于外锥距为R，齿宽为B的弧齿锥齿轮，弧齿锥齿轮中的任意一条球面渐开线所对应的球面半径如下式表示：

Rbi=R-(i-1)B/(n-1)

(9)

弧齿锥齿轮球面渐开线上点Si角度为：

(10)

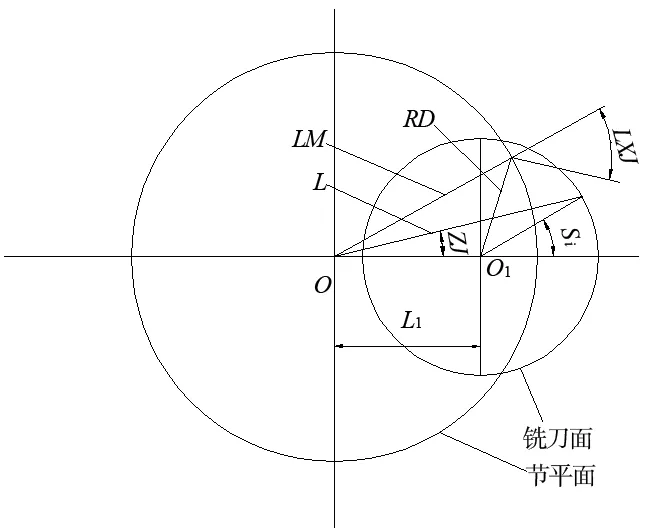
图3 刀盘位置及几何关系

球面渐开线中的点所对应的偏角ZJi为：

(11)

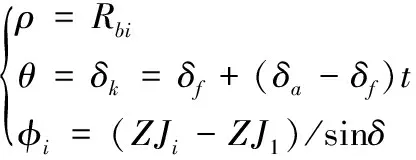
(12)

在坐标系中从大端到任意一条齿形曲线所转过角度为φi，δ为齿轮分度圆锥角，δa为齿顶角。

与其对称一侧球面渐开线如式(13)所示：

(13)

其它参数与式(12)相同。

上面公式是根锥角大于基锥角的情况；当根锥角小于基锥角时，根锥角到基锥角这段曲线用公式表示如下：

θ=δk=δf+(δb-δf)t

(14)

式中,δb为基锥角。

基锥角到齿顶角的这段曲线用式(15)表示：

θ=δk=δf+(δa-δb)t

(15)

式中,δa为齿顶角。

2.2 齿根曲线和齿顶曲线公式

齿根曲线是齿根圆上的一段圆弧，公式如下：

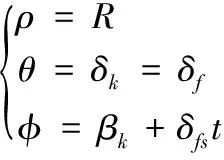
(16)

另一侧齿根曲线表示：

(17)

其它参数与上相同。而齿顶的求解与齿根类似，只需将根锥角换成顶锥角，将根锥齿厚角换成顶锥齿厚角。

2.3 齿形曲线

弧齿锥齿轮的齿面与节锥的交线称之为节线，所有节线是齿轮的纵向齿形。齿面上沿纵向分成h等分，这样齿面上有h条齿形曲线，每条齿形曲线分成t等分，则每条齿形曲线上的i等分的点的偏角为：

Si=S1+(i-1)(Sn-S1)/t

(18)

式中,i从1～t，S1、Sn分别是式(10)中i=1和i=n的取值。

(19)

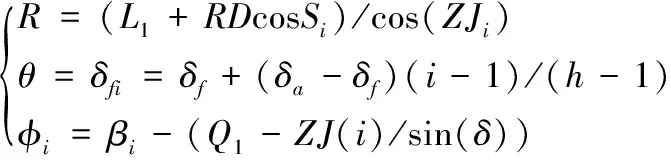
(20)

另一侧的齿形曲线可表示为：

DYi=FYCHJ+2(β-βi)

(21)

φi=βi-(Q1-ZJ(i)/sin(δ))+DYi

(22)

FYCHJ为分度圆齿厚角，β为分度圆偏角，其它参数与式(20)相同。

上述是根锥角大于基锥角情况，当根锥角小于基锥角，则根锥角到基锥角这段曲线公式为：

θ=δfi=δb+(δa-δb)(i-1)/(h-1)

(23)

基锥角到齿顶角的这段曲线公式与根锥角大于基锥角相同。

2.4 齿根过渡曲面

连接齿面和齿根的过渡曲面部分，可以通过倒角圆方法进行优化处理：

(1)当基锥角小于根锥角时，球面渐开线是与齿根曲线相交，则齿根过渡曲面可以采用变半径倒圆角[10]的方法来处理。

Rf=0.3mne

(24)

式中，mne为法向模数。

(2)当基锥角大于根锥角时，弧齿锥齿轮在基圆内没有球面渐开线，则弧齿锥齿轮过渡部分圆角曲线的起点为基圆与球面球面渐开线的交点，终点为基圆与齿根曲线的交点。

3 轮齿有限元网格划分方法

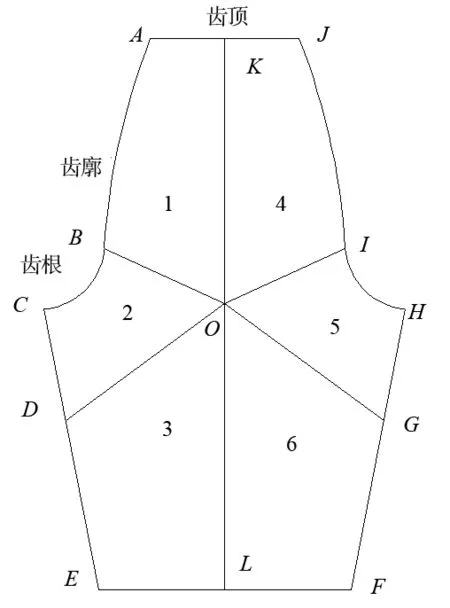
图4 弧齿锥齿轮的轮齿端面分块图

根据轮齿的端面齿廓形状，可以将整个端面划分为6大子块，网格划分的方法如下所述：B点和I点是齿面和齿根过渡曲面分界点，先连接齿顶和齿根的中点K点和L点，然后根据端面的形状确定KL线段中的O点，最后确定轮毂上的侧面的D点和G点的位置，B点和I点是齿面和齿根过渡曲面分界点，分别连接OB、OI、OG、OD、OL、OK，如图4所示。

根据齿廓上渐开线分成的n等分，可将KO分成相应的n等分；齿轮啮合时齿根过渡部分应力集中，这时齿根过渡部分网格划分相对比较密集，OG、DO、EL、LF划分数目与齿根以及齿根过渡部分BC和IH数目相同；将BO、OI、CD、HG划分的等分与齿顶AK与KJ所划分数目相同。

4 实例

以表1中“小轮左旋、大轮右旋”的弧齿锥齿轮副为例，在MATLAB环境下按照上述方法参数化地建立起了弧齿锥齿轮网格模型。

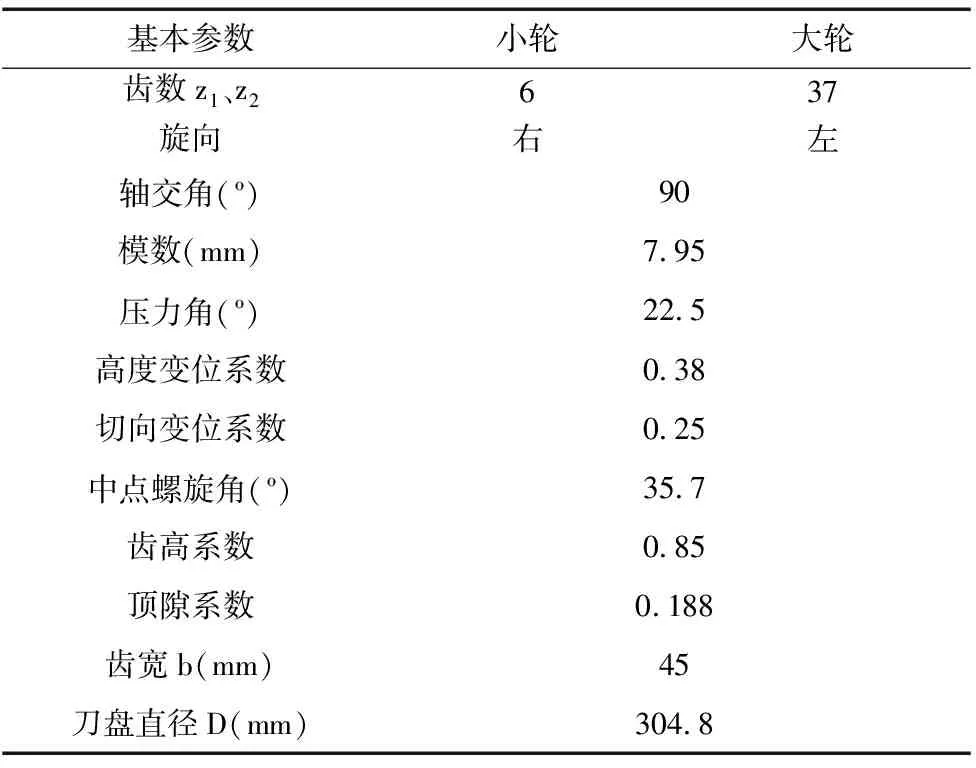
表1 齿轮副的基本参数

Step1:绘出弧齿锥齿轮一个齿面。齿面上沿齿廓方向球面渐开线划分n等分，沿齿向方向划分h等分，本文中n取11，h取9。在MATLAB中根据公式(8)～公式(15)编写参数化程序，将表1中的数据齿数z1、z2等参数代入到上述公式画出11条球面渐开线。在MATLAB中根据公式(18)～公式(23)编写参数化程序，将表1中的数据代入到上述公式画出9条齿形曲线。由11条球面渐开线和9条齿形曲线画出的一个齿面如图5所示。

Step2:确定齿根的过渡曲面。根据公式(24)可以将齿根的过渡曲面画出来。齿面和齿根的过渡曲面如图6所示。