非相对论分子物理中带逆平方势的非线性Schrödinger方程的解整体存在性

夏 滨

(四川建筑职业技术学院 教务处, 四川 德阳 618000)

1 预备知识

在非相对论分子物理中带磁性的粒子捕获电子是一类重要的物理现象.关于它的刻画、研究和掌控有着重要的意义和作用.这类现象由一类带逆平方势的非线性Schrödinger方程[1-2]模拟,其形式如下

x∈RD,

(1)

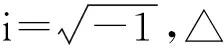
方程(1)中的逆平方势强烈地影响着相应的Schrödinger算子,因为它有与Schrödinger算子相同的尺度不变性和Kelvin变换,从而使得它不属于Kato类[3-4].因此方程(1)吸引了众多关注和研究[5-7].

赋予方程(1)初值

φ(x,0)=φ0,x∈RD.

(2)

(3)

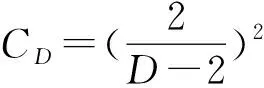
(爆破).

本文特别感兴趣Cauchy问题(1)～(2)的解整体存在性问题.采用文献[11-12]的方法,通过考察Cauchy问题(1)～(2)的特征以及它的哈密尔顿系统不变量,并结合一系列的精细不等式工具,建立了Cauchy问题(1)～(2)的解整体存在性.对于次临界情形,证明了系统的解全部整体存在；对于临界情形,获得了系统解整体存在的一个L2标准；对于超临界情形,获得了系统整体存在的一个H1标准.进一步,这些标准都是精确、显示和可计算的.

2 预备知识和主要结论

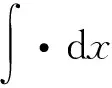
定义质量泛涵

势能泛涵

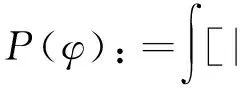
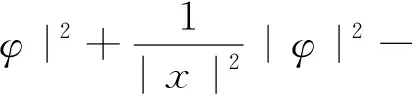
和能量泛涵

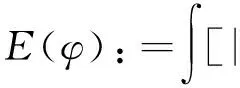
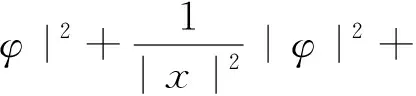
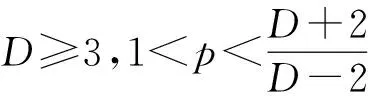
M(φ(t))=M(φ0)

(4)

和

P(φ(t))=P(φ0),

(5)

其中M和P是前面定义的质量和势能泛涵.

设Q(x)是如下非线性椭圆方程的正径对称解

-△u+u-|u|p-1u=0,u∈H1(RD).

(6)

文献[14]建立了其解的存在性,文献[15]证明了其解的唯一性.

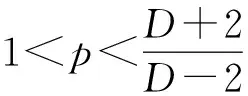
(7)

其中,最佳系数C*>0满足

(8)

引理2.2(Young不等式)[17]对任意正实数a>0,b>0,ε>0,假设r,r′∈(1,+∞)且满足1/r+1/r′=1.那么

证明对于函数f(x)=x-Cxθ,x>0,其中θ∈(0,1)和C>0,有

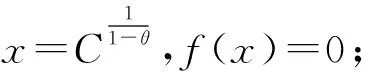
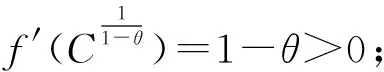
3)f″(x)=Cθ(1-θ)xθ-2>0,x>0.

另一方面,函数f(x)的Taylor展式如下

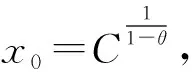
下面给出本文的主要结论.

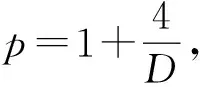
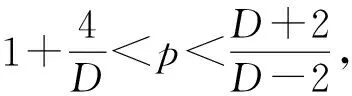
‖φ0‖H1<

那么其解φ在H1(RD)中都整体存在.

3 次临界和临界情形

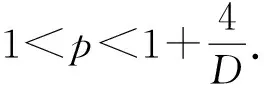
P(φ0)=P(φ)=

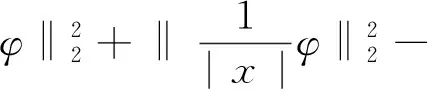
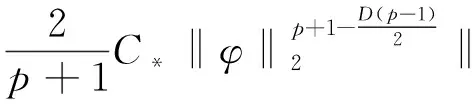
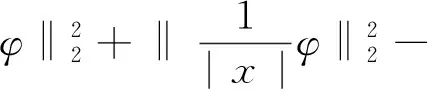
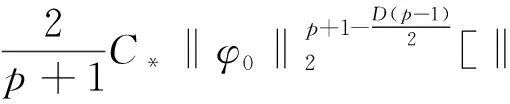
(9)

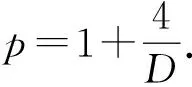
▽φ|2+

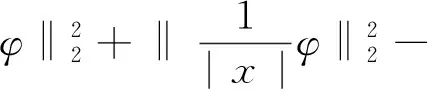
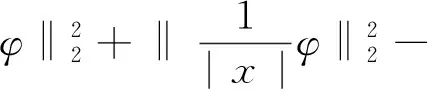
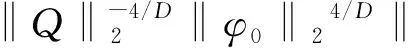
(10)

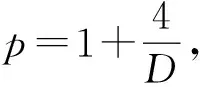
4 超临界情形

首先,建立Cauchy问题(1)～(2)的发展不变流.设置

▽u|2dx<

其中E是第二节中定义的能量泛涵,Q是方程(6)的正径对称解.

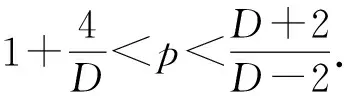
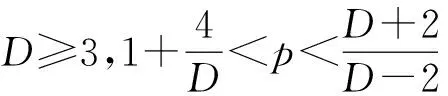
M(φ(t))=M(φ0),t∈[0,T).

因此

E(φ0)=P(φ0)+M(φ0)<

从而

E(φ(t))=P(φ(t))+M(φ(t))<

(11)

为了证明φ(t)∈Kg,只需证明

(12)

如果(12)式不成立,由

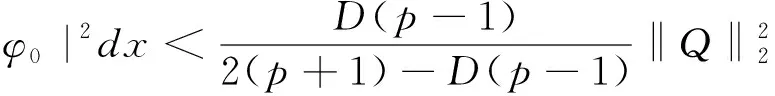
和连续性,存在t1∈(0,T)使得

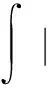
▽φ(t1)|2dx=

(13)

然而,由引理2.1得

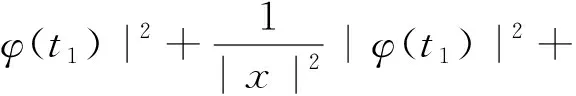
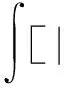
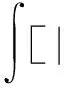
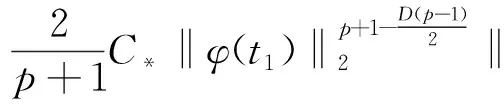
(14)

这里,C*是引理2.1中Gagliardo-Nirenberg不等式的最佳系数.运用Young不等式(引理2.2)可得

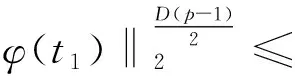
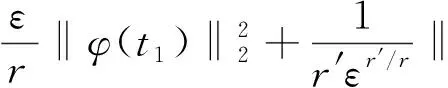
(15)

这里

(16)

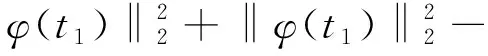
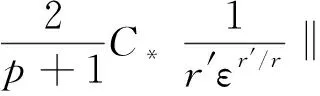
(17)

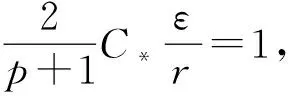
(18)

那么

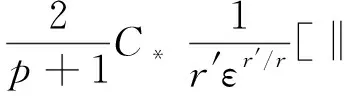
(19)

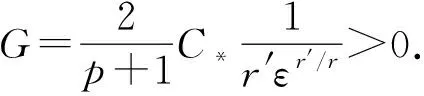
在s∈(0,+∞)上定义实值函数

∀s>0.

(20)

于是有

因此,当s∈(0,+∞),F(s)达到它的最大值

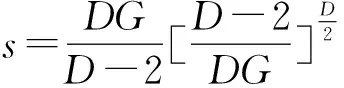
(21)

有

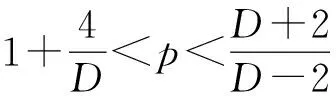
(22)

因此,由(13)、(19)～(22)式可得

(23)

这与

E(φ(t1))=E(φ0)<

矛盾，因此(12)式成立.因此,Kg在Cauchy问题(1)～(2)生成的流上是不变的.

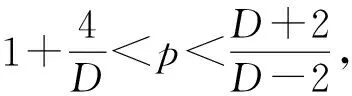
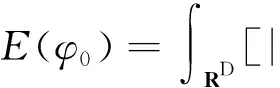
且

那么Cauchy问题(1)～(2)的解φ在H1(RD)中整体存在.

证明设初值φ0∈H1(RD)满足

和

那么φ0∈Kg.让φ表示Cauchy问题(1)～(2)在t∈[0,T)上的解.由命题4.1知φ∈Kg，因此

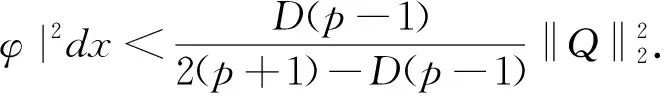
(24)

同时,注意到质量守恒律(4),易得φ在H1(RD)中有界.因此,由局部适定性结论,此情形下的Cauchy问题(1)～(2)的解φ在H1(RD)中都整体存在.

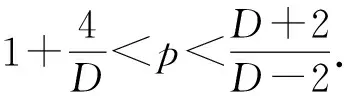
▽φ0|2+|φ0|2]dx]1/2<

(25)

那么可得

▽φ0|2+|φ0|2]dx<

(26)

即

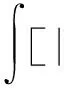
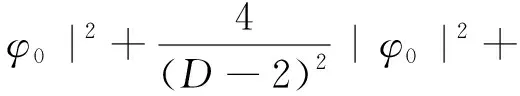
(27)

从而,由(3)式知

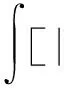
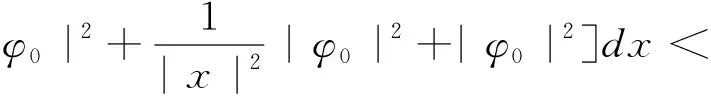
(28)

于是

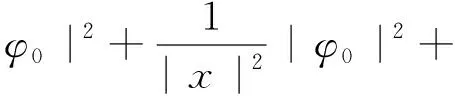
(29)

为了证明定理2.3,由命题4.2,只需证明

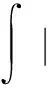
▽φ0|2dx<

(30)

然而,由(28)式易得

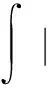
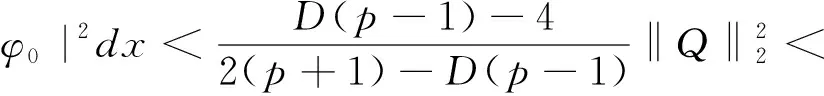
(31)

因此,由(29)、(31)式和命题4.2可知Cauchy问题(1)～(2)的解φ在H1(RD)中整体存在.