内蕴群范畴中的乘积性质

张凯强, 汤建钢

(伊犁师范学院 数学与统计学院, 新疆 伊宁 835000)

20世纪60年代,Ehresmann[1]提出了Internal Category理论,到目前为止已经成为范畴理论的重要组成部分[1-7].Lawever[2]在他的论文中为了使范畴中的对象具有代数结构,引入了范畴中的内蕴群对象概念,进一步揭示了事物的内在特性.内蕴范畴理论是研究范畴中逻辑真实存在的内蕴结构,如代数结构、序结构、拓扑结构以及混合结构.群是具有代数结构的数学对象,利用范畴语言,可以在具有有限乘积范畴中表达群的代数结构,也就是内蕴群对象.

内蕴群对象在不同的范畴中有不同的表示,如在集合范畴中的内蕴群对象就是通常所说的群,在群范畴中的内蕴群对象则是2-群[3-4],在拓扑空间范畴中的内蕴群对象就是拓扑群,在Hausdorff空间范畴中的内蕴群对象就是Hausdorff群,而在Diff范畴中的群对象则是李群[5-6].

结合文献[8]中的相关定理及思路,本文从范畴的角度出发[9-11],引入了内蕴群范畴的概念,讨论了内蕴群范畴中的乘积性质,证明了关于乘积封闭的范畴的内蕴群范畴也是乘积封闭的.

本文引用文献[3,11]中的记号.

1 预备知识

本文中用C表示具有有限乘积的范畴,T表示其终对象,I表示以集合元素为指标的指标集.

参考文献[3]引入内蕴群对象以及内蕴群范畴的概念.

定义1.1[3]设范畴C具有有限乘积,T是范畴C中的终对象.

1) 四元组G=(C,μ,η,ζ)被称为C中的一个群对象,如果C是范畴C中的一个对象,乘积态射μ、单位态射η和逆态射ζ分别是范畴C中的态射,μ:CΠC→C,η:T→C,ζ:C→C,使得下图交换:

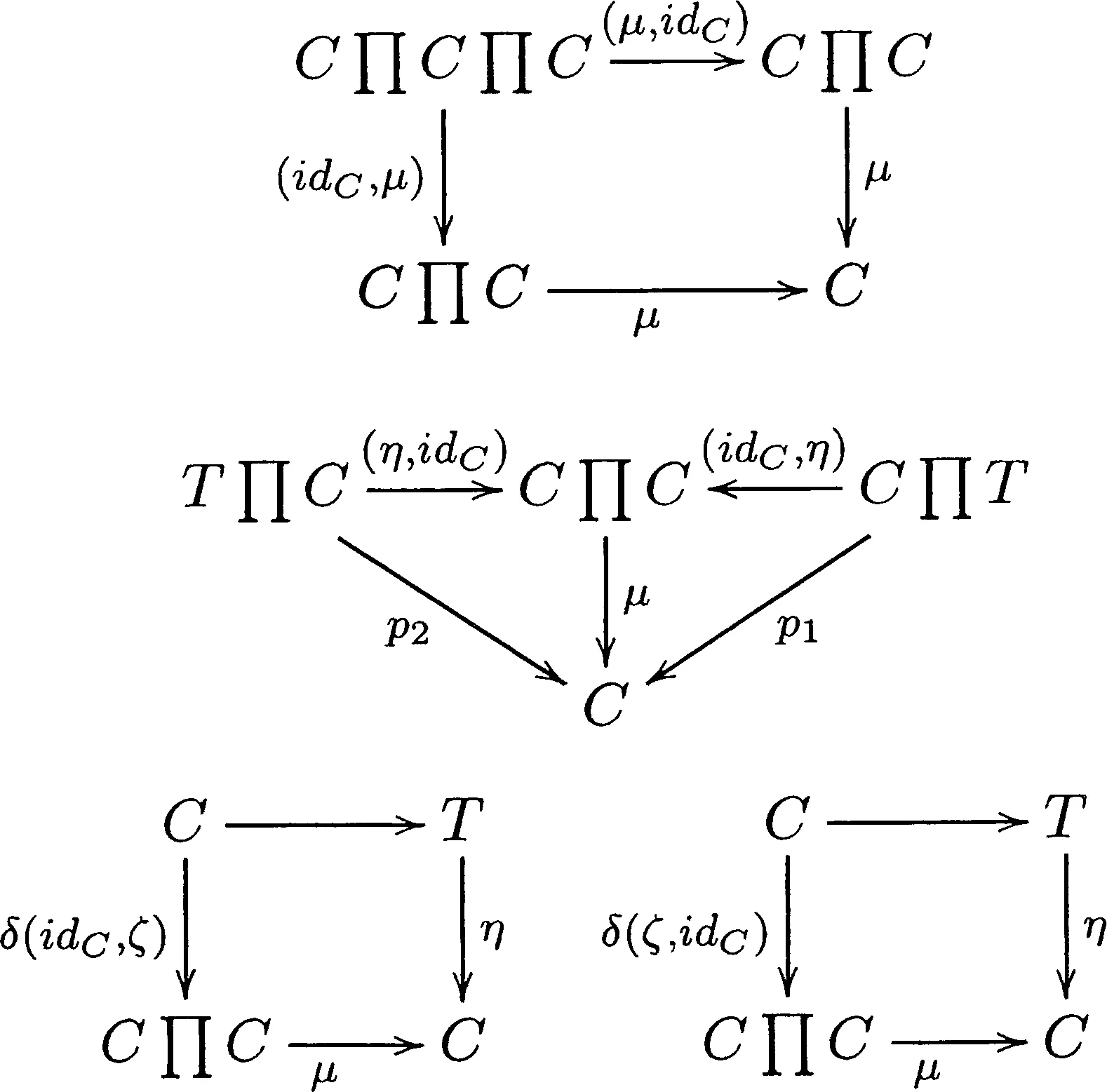
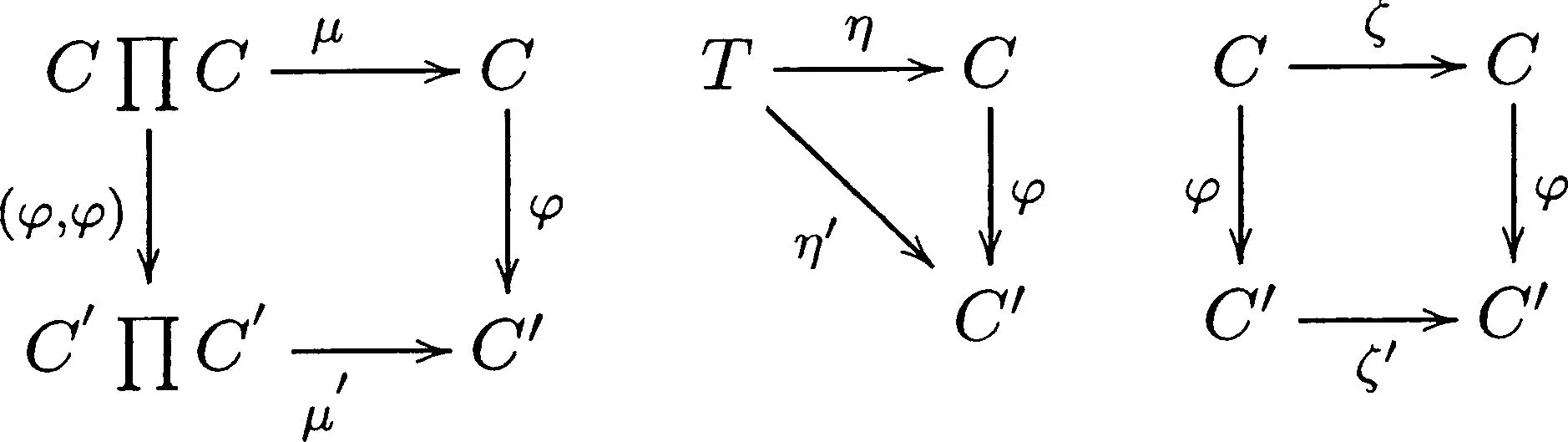
2) 设G=(C,μ,η,ζ)和G′=(C′,μ′,η′,ζ′)是范畴C中的2个群对象.一个内蕴群同态φ:G→G′是C中的态射φ:C→C′,使得下图交换:

3) 设G=(C,μ,η,ζ),G′=(C′,μ′,η′,ζ′)和G″=(C″,μ″,η″,ζ″)是范畴C中的群对象,φ:G→G′和ψ:G′→G″是范畴C中的内蕴群同态,则φ和ψ的复合是内蕴群同态φ∘ψ:G→G″,由范畴C中的态射φ∘ψ:C→C″所定义.

4) 设G=(C,μ,η,ζ)是范畴C中的一个群对象.单位内蕴群同态idG:G→G被定义为范畴C中的单位态射idC:C→C.

定理1.1[7]设C是一个具有有限乘积的范畴,则以C中的内蕴群对象为对象,以内蕴群同态为态射构成一个范畴,记作Grp(C).

在讨论内蕴群范畴Grp(C)中的乘积时,为了讨论方便,统一地给出在一个一般范畴C中的乘积定义.

定义1.2[8]设C是一个范畴,{Ci}i∈I⊆ Obj(C)是范畴C中的对象族,则诸Ci的一个乘积为集合{C,pi|i∈I},其中C∈Obj(C),pi∈Mor(C,Ci),i∈I,使得如果B∈Obj(C),gi∈Mor(B,Ci),i∈I,则存在唯一的r∈Mor(B,C),使得∀i∈I,下图交换,即∀i∈I,pi∘r=gi.

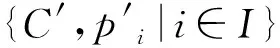
引理1.1[9]设范畴C存在任意乘积.{fi:Ai→Bi|i∈I}是C中的一族态射(I是集合),{pj:ΠAi→Aj|j∈I}与{qj:ΠBi→Bj|j∈I}分别是{Ai}i∈I与{Bi}i∈I的乘积,则存在唯一的态射Πfi:ΠAi→ΠBi使得下图交换成立:

引理1.2设范畴C存在任意乘积,{Ai}i∈I与{Bi}i∈I是范畴C中的对象族,{pj:ΠAi→Aj|j∈I}与{qj:ΠBi→Bj|j∈I}分别是对象族{Ai}i∈I与{Bi}i∈I的乘积,那么{(pj,qj):(ΠAi)×(ΠBi)→Aj×Bj|j∈I}是对象族{Ai×Bi}i∈I的乘积.

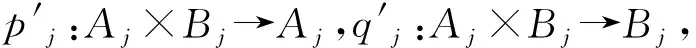
则下面图也交换:

故原命题成立,证毕.

引理1.3设范畴C存在任意乘积,{Ai}i∈I与{Bi}i∈I是范畴C中的对象族,{pj:ΠAi→Aj|j∈I},{qj:ΠBi→Bj|j∈I}和{rj:Π(Ai×Bi)→Aj×Bj|j∈I}分别是对象族{Ai}i∈I、{Bi}i∈I与{Ai×Bi}i∈I的乘积,则存在唯一的同构δ:(ΠAi)×(ΠBi)→Π(Ai×Bi)使得下图交换:

证明只需注意到{rj:Π(Ai×Bi)→Aj×Bj|j∈I}是乘积对象族{Ai×Bi}i∈I的乘积,利用引理1.2和定理1.2即得结论.

推论1.1设范畴C存在任意乘积,{Ai}i∈I与{Bi}i∈I是范畴C中的对象族,则存在唯一同构δ:(ΠAi)×(ΠBi)→Π(Ai×Bi).

由定义1.2和引理1.3可以得到以下结论.

引理1.4设范畴C存在任意乘积,{Ai}i∈I、{Bi}i∈I和{Ci}i∈I是范畴C中的对象族,{fi:Ai×Bi→Ci|i∈I}是范畴C中的一族态射,则存在唯一的态射f:(ΠAi)×(ΠBi)→ΠCi使得下图交换:

定理1.3[11]若T与T′是范畴中的2个终对象(初始对象),则T与T′同构.

引理1.5设T是范畴C中的终对象,ΠT是其终对象的乘积,则ΠT≌T.

证明由于ΠT是若干T在范畴C中的乘积,故存在态射t:T→ΠT使得下图对于任意的i∈I交换：

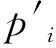
又由于T是范畴C中的终对象,故存在态射s:ΠT→T使得下图也交换:

把t和s复合后,关于每个i∈I都有以下的交换图:

根据定理1.3唯一性条件,必须有s∘t=idT,类似地有t∘s=idΠT.因此ΠT≌T.

2 主要结果

定理2.1若范畴C关于任意乘积封闭,则内蕴群范畴Grp(C)关于任意乘积也封闭.

证明设{Ci}i∈I是内蕴群范畴Grp(C)中的一族对象,则{Ci}i∈I是范畴C的一族对象.由于范畴C存在任意乘积,所以{Ci}i∈I在范畴C中存在乘积,不妨设乘积为{pi:C→Ci|i∈I}.由于诸Ci为内蕴群对象,根据定义1.1,可设内蕴群对象Ci的乘积态射为μi:Ci×Ci→Ci,单位态射为ηi:T→Ci,逆态射为ζi:Ci→Ci,记C=ΠCi,μ=Πμi:Π(Ci×Ci)→ΠCi,η=Πηi:ΠT→ΠCi,ζ=Πζi:ΠCi→ΠCi.根据引理1.3可知,Π(Ci×Ci)⋍(ΠCi)×(ΠCi),不妨设为δ:(ΠCi)×(ΠCi)→Π(Ci×Ci),根据引理1.4,则下图是交换的:

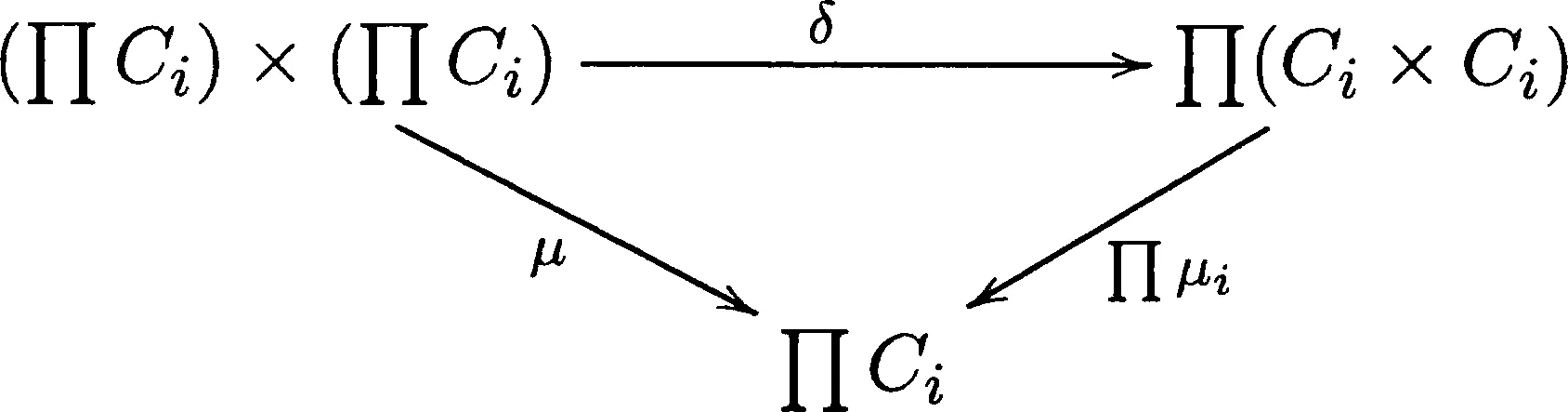
即μ=(Πμi)∘δ,在同构意义下μ=Πμi.

现在证明G=(ΠCi,μ,η,ζ)是范畴C中的内蕴群对象,即G∈Obj(Grp(C)).

由于Gi=(Ci,μi,ηi,ζi)∈Obj(Grp(C)),根据定义1.1,所以下图是交换的:

因此,下图也可换:

根据引理1.3,对于∀i∈I,Π(Ci×Ci×Ci)≌(ΠCi)×(ΠCi)×(ΠCi),Π(Ci×Ci)≌(ΠCi)×(ΠCi).再由引理1.4,所以可以得到下图是交换的:

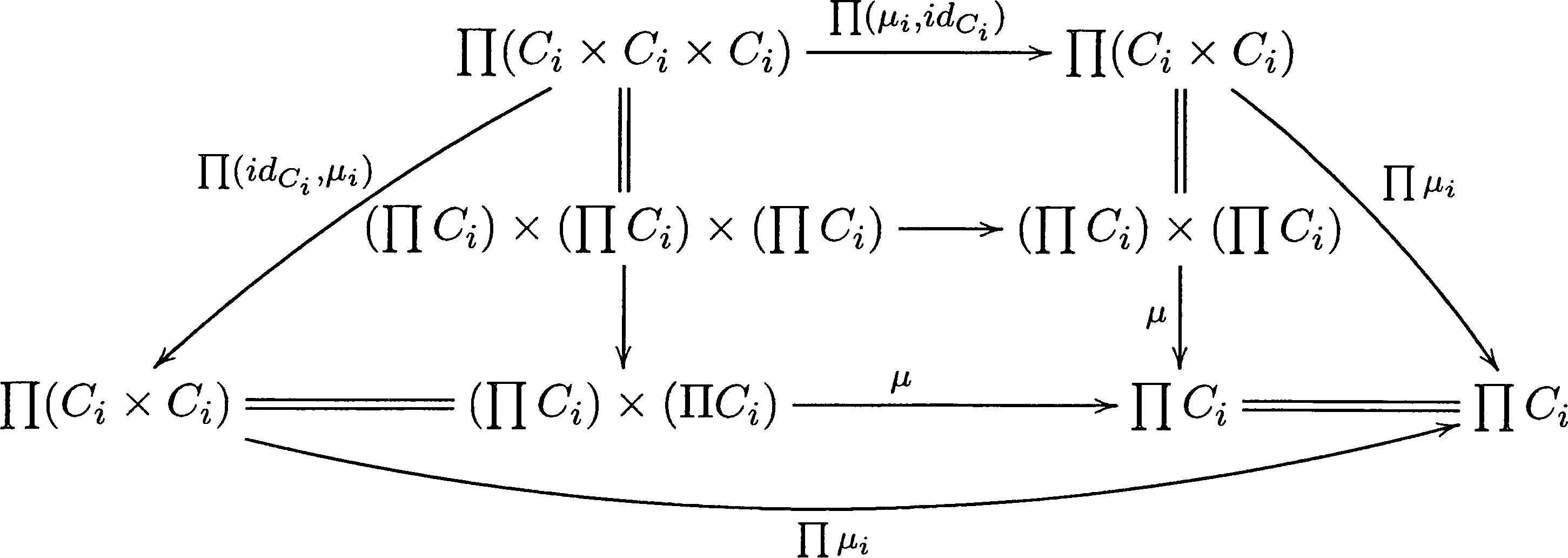
于是得到图1是可交换的:

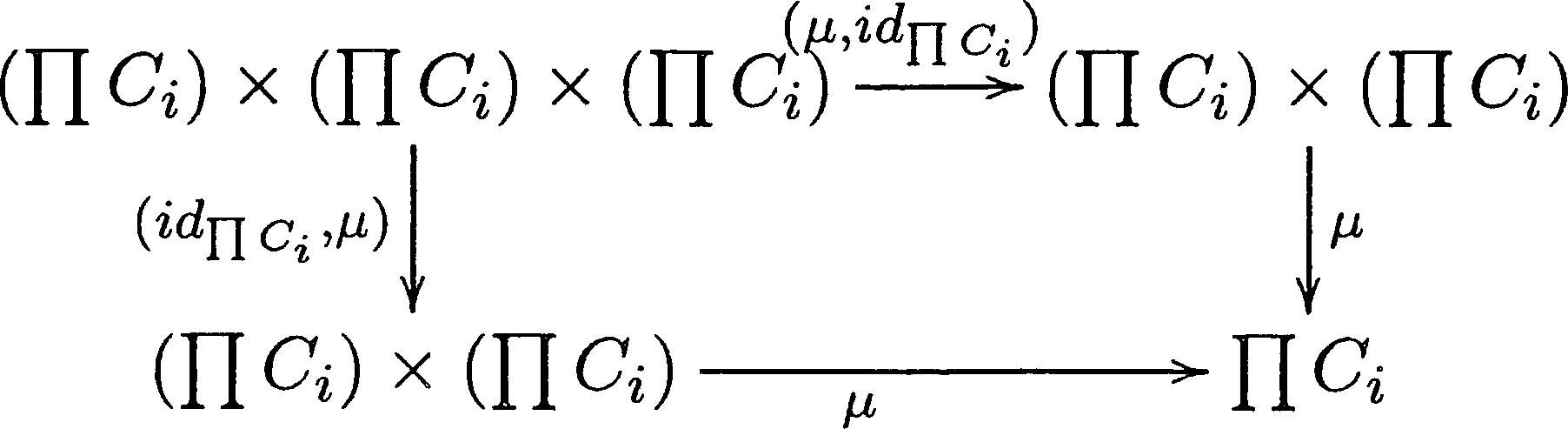
图 1

由于对于∀i∈I,有下图交换:

所以下图也交换:

根据引理1.3以及引理1.5可知,对于∀i∈I,Π(T×Ci)≌(ΠT)×(ΠCi)≌T×(ΠCi),Π(Ci×T)≌(ΠCi)×(ΠT)≌(ΠCi)×T,再由引理1.4,故可以推出下图是可交换的:

于是能得到图2是可交换的

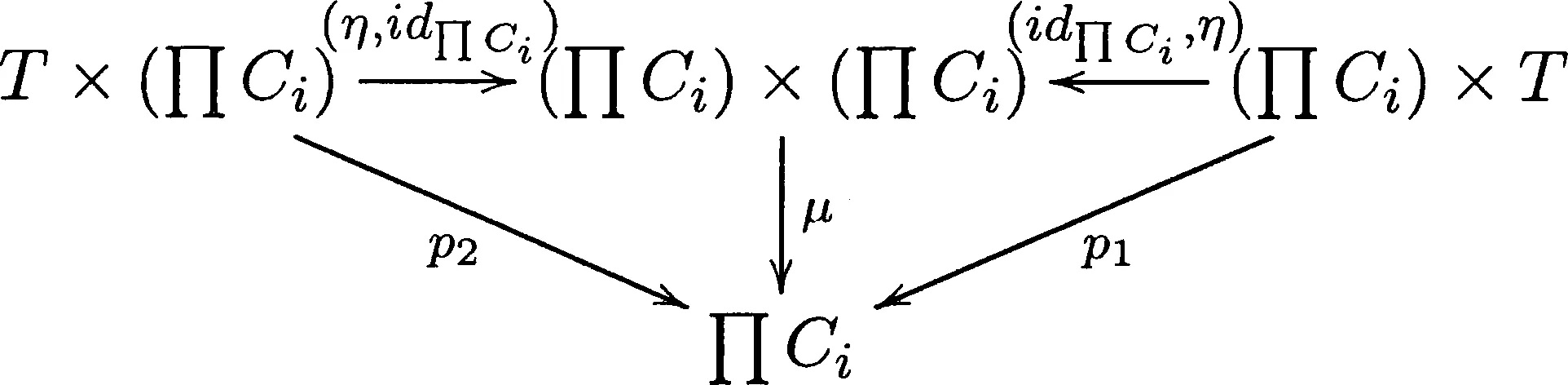
图 2

对于∀i∈I,由定义1.1推广可以得到下图是可交换的:

那么能知道下图也是可交换的:

由引理1.5可知ΠT≌T,则下图是交换的:

再根据引理1.3和引理1.4,故能推出下图是可交换的:

因此,图3也是可交换的.

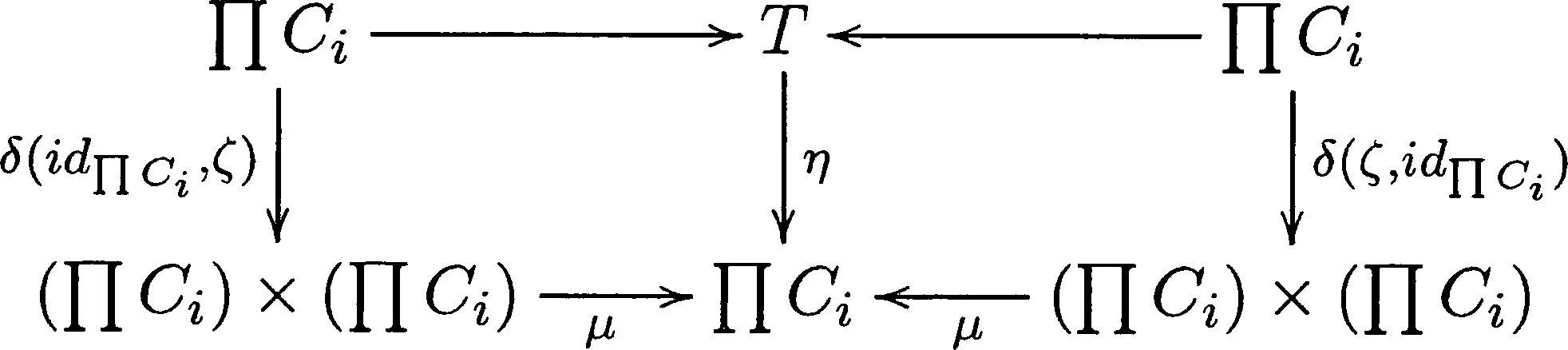
图 3

由于图1～3分别可交换,对应于定义1.1中的1),对于∀i∈I,即ΠCi∈Obj(Grp(C)),因此G=(ΠCi,μ,η,ζ)是范畴C中的内蕴群对象.

以下证明投射所构成的态射族{pi:ΠCi→Ci|i∈I}是内蕴群范畴Grp(C)中的态射族,首先证明图4交换：

图 4

即∀i∈I,μi∘(pi×pi)=pi∘μ.

根据引理1.1、引理1.3以及引理1.4,可知下图是可交换的:

ri是Π(Ci×Ci)→Ci×Ci的投射所构成的态射族.因此,图4是可交换的.

其次,令μ=Πμi:Π(Ci×Ci)→ΠCi,η=Πηi:T→ΠCi,ζ=Πζi:ΠCi→ΠCi,由于∀i∈I,ηi:T→Ci为单位态射,η=Πηi,根据引理1.1,则下图是交换的:

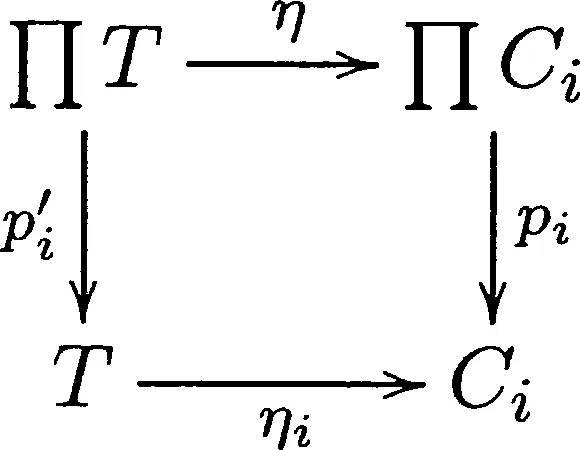
图 5

又由于∀i∈I,ζi:Ci→Ci为逆态射,ζ=Πζi,根据引理1.1,则图6是交换的.

图 6

图4～6分别可换,对应于定义1.1中的2),故{pi:ΠCi→Ci|i∈I}⊆Mor(Grp(C)).

任取一族内蕴群对象Ci∈Obj(Grp(C)),i∈I,由于内蕴群范畴Grp(C)是范畴C的子范畴,所以Ci∈Obj(C),i∈I,又由于范畴C对任意乘积封闭,所以诸Ci在范畴C中存在乘积,不妨设为{pi:ΠCi→Ci|i∈I}.由于Ci∈Obj(Grp(C)),根据以上的证明可知,ΠCi∈Obj(Grp(C)),i∈I,pi∈Mor(Grp(C)),i∈I.

以下证明{pi:ΠCi→Ci|i∈I}是诸Ci在内蕴群范畴Grp(C)中的乘积.

由于{pi:ΠCi→Ci|i∈I}是范畴C中的乘积,如果在内蕴群范畴Grp(C)中任取对象B和态射族{gi:B→Ci|i∈I},则B是范畴C中的对象,pi是范畴C中的态射,因为范畴C存在任意乘积,不妨设为{gi:B→Ci|i∈I}.根据定义1.2,故在范畴C中存在唯一的态射r:B→ΠCi,使得下图是交换的:

要证明{pi:ΠCi→Ci|i∈I}是内蕴群范畴Grp(C)中的乘积,只需证明r∈Mor(Grp(C))即可.令内蕴群对象B的乘积态射为μ′:B×B→B,单位态射为η′：T→B,逆态射为ζ′:B→B.由于内蕴群对象Ci,i∈I的乘积态射为μi:Ci×Ci→Ci,根据定义1.1,则对于∀i∈I有下图是可交换的:

又由于图4是交换的,故能得到下图也交换:

因此对于∀i∈I有如下式子成立:

pi∘r=gi,

(1)

μi∘(pi×pi)=pi∘μ,

(2)

μi∘(gi×gi)=gi∘μ′.

(3)

根据(1)～(3)式可推出

pi∘r∘μ′=gi∘μ′=

μi∘(gi×gi)=

μi∘((pi∘r)×(pi∘r))=

μi∘((pi×pi)∘(r×r))=

pi∘μ∘(r×r).

由于∀i∈I,pi∘r∘μ′=pi∘μ∘(r×r),根据pi的集体单性质,有r∘μ′=μ∘(r×r)成立,即有图7是交换的.

由于η′:T→B是内蕴群对象B的单位态射,ηi:T→Ci是内蕴群对象Ci的单位态射,根据定义1.1,因此对于∀i∈I有下图是交换的:

又由于图5是交换的,所以有下图是交换的:

因此对于∀i∈I有如下式子成立:

pi∘r=gi,

(4)

gi∘η′=ηi,

(5)

pi∘η=ηi.

(6)

根据(4)～(6)式可推出

pi∘r∘η′=gi∘η′=ηi=pi∘η.

由于∀i∈I,pi∘r∘η′=pi∘η,根据pi的集体单性质,有r∘η′=η式成立,即有图8是交换的:

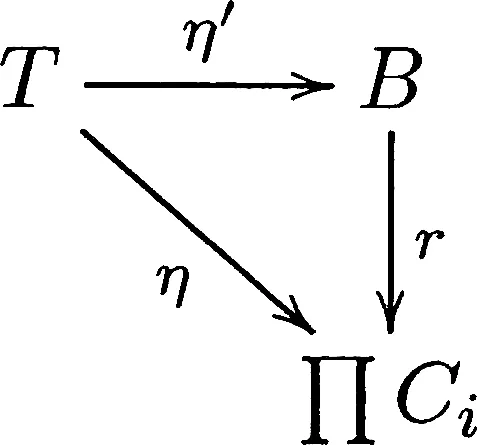
图 8

由于内蕴群对象B的逆态射为ζ′:B→B,内蕴群对象Ci的逆态射为ζi:Ci→Ci,根据定义1.1,因此有下图是交换的:

又由于图6是交换的,所以下图是交换的:

因此对于∀i∈I有如下式子成立:

pi∘r=gi,

(7)

gi∘ζ′=ζi∘gi,

(8)

ζi∘pi=pi∘ζ.

(9)

根据(7)～(9)式可推出

pi∘r∘ζ′ =gi∘ζ′=ζi∘gi=

ζi∘pi∘r=pi∘ζ∘r.

由于∀i∈I,pi∘r∘ζ′=pi∘ζ∘r,根据pi的集体单性质,有r∘ζ′=ζ∘r式成立,即有图9是交换的.

图 9

图7～9分别可交换,对应于定义1.1中的2),故r∈Mor(Grp(C)).由定理1.2,态射r在范畴C的唯一性,可知态射r在内蕴群范畴Grp(C)中也唯一.因此,内蕴群范畴Grp(C)中存在唯一的态射r使得下图交换:

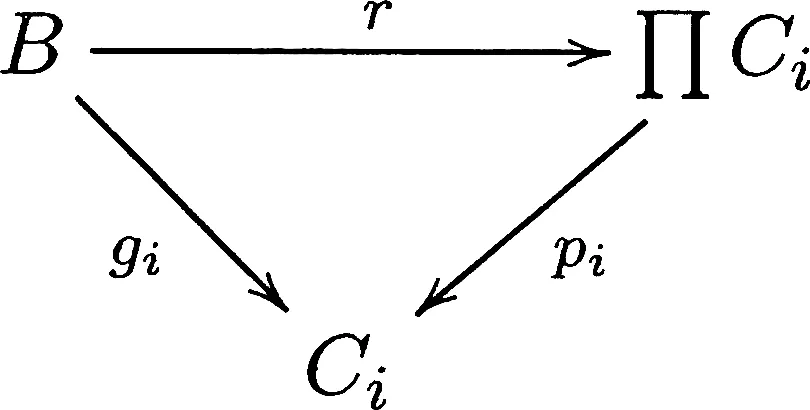
综上所述,诸Ci∈Obj(Grp(C)),i∈I在范畴C中的乘积{pi:ΠCi→Ci|i∈I}也是内蕴群范畴Grp(C)中的乘积,即内蕴群范畴Grp(C)关于任意乘积是封闭的.证毕.

致谢伊犁师范学院2016研究生科研创新项目(2016YSY011)对本文给予了资助,谨致谢意.