基于绿色供应链利益分配的P-DEA与Shapley值模型

刘佩，高更君

基于绿色供应链利益分配的P-DEA与Shapley值模型

刘佩，高更君

(上海海事大学 物流研究中心，上海 201306)

基于风险偏好下的机会约束DEA(P-DEA)模型理论和联盟博弈的Shapley值方法，利用P-DEA模型对Shapley值进行修正，并依据各成员对绿色供应链系统的相对贡献程度，设计联盟利益在各参与者之间进行公平分配的机制，通过案例分析进行模型有效性的验证。研究结果表明：利用P-DEA修正的Shapley值与参与者的相对贡献程度更吻合，且考虑了参与者的风险偏好以及投入、产出重要性，使得分配结果更加符合实际情况，维持了供应链的稳定。

绿色供应链；P-DEA；Shapley值；利益分配；联盟博弈

随着绿色消费者的扩张，绿色市场的增长，绿色技术的升级和政府的支持加强，越来越多的企业组成绿色供应链研发联盟，旨在生产出环境友好度更高的绿色产品[1]。对于供应链上的成员而言，他们建立联盟的目的是在实现环境效益的同时能够提高经济利益，但每个参与者的最终利益分配结果还受到参与者风险态度等行为因素的影响[2]。因此，考虑成员风险偏好下的利益分配模型将更加贴近实际。对于资源(利益)分配问题，国内外学者已经用不同的方法做了大量的研究，其中利用DEA法和Shapley值法解决资源分配问题是比较常见的有效方法，李勇军等[3]基于DEA与联盟博弈方法研究了成本分摊问题，证明了将成本作为新的投入时DEA有效，并提出了Shapley值的成本分摊方法；丁乐群等[4]使用DEA联盟博弈Shapley值法求解在限定的权重范围内直购电用户转运费中成本的分摊问题；李维乾等[5]基于DEA合作博弈法研究了流域水源生态补偿分摊额，利用梯形模糊数方法改进了Shapley值解，为流域的生态补偿额的合理分摊提供了方法参考；而YANG等[6]基于DEA的最优效率值设计了新的特征函数，考虑成员在加入联盟前后对原有联盟子集效率值和自身的效率值的影响提出了一种修改的Shapley值来公平地解决资源分配问题。虽然这些研究结合了DEA和Shapley值法各自的特点，但大多是将资源纳入内生因素，即将分配的资源放入参与者的投入或产出中，再依据一定原则进行分配，且没有考虑到参与成员在联盟时存在的风险。由于风险的主要表现特征为不确定性，而确定型DEA是根据已知数据集进行的决策，不一定能较好的描述参与者的风险偏好[7]。鉴于此，本文基于绿色供应链利益分配背景下，将供应链上供应商和制造商参与研发联盟创造的利益看做外生因素，利用考虑了参与者投入产出重要性和风险偏好的机会约束DEA(P-DEA)模型与合作博弈的Shapley值法进行结合，通过联盟博弈下的P-DEA模型求出各参与成员在不同联盟组织的效率值，并以此来修改Shapley值的特征函数，得到一个的Shapley值模型。最后运用Lingo进行编程求解，通过案例分析进行模型验证，以保证模型的有效性。

1 研究背景

绿色供应链是以绿色产品生产为主，涉及链上的多家供应商与制造商，其目的是使得产品从原材料采购、制造、包装的整个过程能够对环境的负面影响最小，资源效率最高。在经济全球化的格局下，供应商已经成为企业的战略联盟者，凭借制造商与供应商的合作伙伴关系，可以有效实施研发合作以降低成本，扩大市场占有率，最终提高整条链的竞争力[8]。对于绿色供应链上的每个供应商和制造商而言，合作研发的目的是为了保障产品既能够达到绿色研发进步又能够实现自身利益最大及供应链整体最优。由于绿色供应链上的原材料供应商和制造商有很多家，成员之间的合作形式也会有很多种，当供应链上的成员形成全联盟时，合作研发的效益将达到最大，创造的经济利益也将达到最优，但如何公平合理地分配这一共同研发利益将是实现绿色供应链协调与联盟稳定的最终着眼点。因此，在绿色供应链系统中，利益分配问题一直是影响研发联盟稳定性的一个关键因素，也受到了越来越多专家学者的关注。传统的Shapley值是用于解决利益分配问题比较常见的一种方法，但由于联盟博弈Shapley值没有考虑到参与者的投入产出重要性以及参与者在进行联盟时存在着风险偏好，本文尝试利用考虑了参与者风险偏好的机会约束DEA模型对其进行修改。机会约束DEA模型打破了传统DEA模型对决策单元具有确定投入和产出数据的约束，允许决策单元(参与者)的投入、产出在一个足够小的概率下超出前沿面[9]，对于面向产出的机会约束DEA模型，则有[10]：

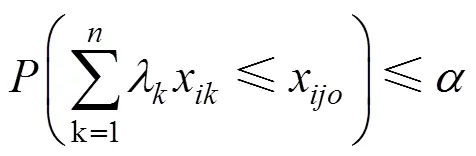
式(1)表示参与者在限定各单元投入的同时，允许评价单元的产出以的概率超出前沿面，通常设定为0.05。

2 模型的建立

2.1 考虑决策者风险偏好的机会约束DEA(P-DEA)模型

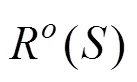
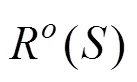
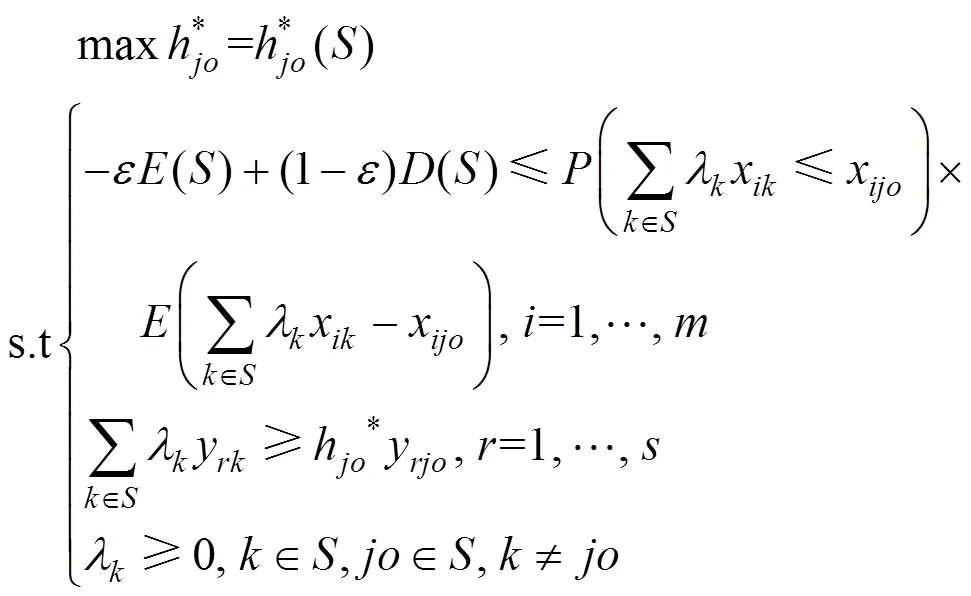
2.2 Shapley值法

2.3 基于P-DEA修正的Shapley值模型

2.3.1 基于P-DEA定义的特征函数

由于P-DEA模型中的最优效率值会随着联盟组织中参与成员的不同而变化，因此，可以利用P-DEA模型对Shapley值中的特征函数进行重新定义：

式(6)证明了新特征函数同时满足超可加性，具体证明过程参考文献[6]。

2.3.2 修正的Shapley值模型

对于一条含有个成员企业的绿色供应链中，各成员之间通过协作结成联盟，在给定的风险偏好下，基于P-DEA修正的Shapley值模型如下：

模型(7)中，为绿色供应链成员企业()加入联盟子集后，给中原有的参与者带来的效率影响程度，其值越大，说明企业的有效性程度就越高；而为参与者自身效率变化百分比，显然其值越小企业就越有效，两者的比值得到的是企业对联盟子集作出的贡献率；为加权因子，表示联盟出现的概率；为每个成员企业对整个联盟系统的平均贡献率。由于为平均贡献率，体现的是绿色供应链上联盟内部各参与者对联盟的相对贡献程度大小，因此需要将这种相对贡献程度转化为各参与成员对联盟的相对贡献率：

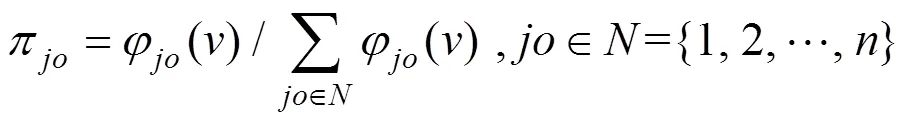
若绿色供应链上的参与者形成全联盟下的最大化收益为，则各参与者可以获得的收益分配 额为：

3 模型求解

根据式(3)，可以利用考虑了参与者风险偏好的机会约束DEA模型中的最优效率值来衡量参与者的收益贡献，由于在合作研发的过程中，绿色供应链上的成员企业可以自由结合形成不同的联盟，且参与者在不同的联盟子集中的效率值也存在差异，因此需要求解出P-DEA联盟博弈模型中各参与者在不同联盟子集中的最优效率值。

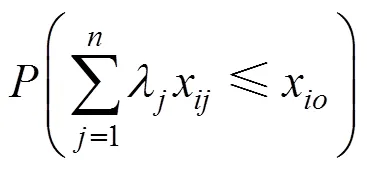
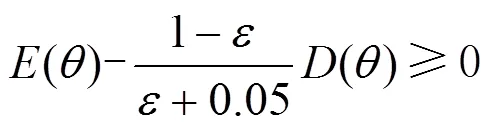
根据模型(11)和修正的Shapley值模型，可以通过以下步骤求解绿色供应链上各参与者在建立合作研发平台时所获得的最优经济利益。

步骤1：写出绿色供应链上个参与者可能组成的所有联盟；

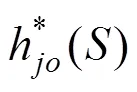
步骤4：根据式(8)~(9)和绿色供应链上参与者合作研发创造的最大化利益，可以分别获得各参与者对联盟系统的相对贡献程度及最终收益分 配额。

4 案例分析

根据模型(11)、(7)以及式(8)~(9)，假设绿色供应链上3个参与者的风险偏好为风险中立，即=0.5，利用Lingo进行编程求解可以得到各成员企业在不同联盟情况下的最优效率值和利益分配结果，见表2~3(概率=0.05)。

表1 供应商和制造商建立合作研发平台的投入、产出数据

表2 不同联盟组织中各参与者的效率值

表3 联盟参与者对联盟整体的贡献和利益分配额

由表4可知，供应商1和制造商3的联盟效率值随着风险偏好程度的增加而递减，风险偏好程度越高得到的利益分配额越多；而供应商2为风险偏好者机会约束有效，效率值不因风险偏好程度的改变而改变，这说明供应商2越考虑风险偏好，对联盟的贡献也越来越大，这可从表4中得到的利益分配额不断增加得到印证。根据分析可知，供应商1与制造商3属于风险规避型参与者，供应商2属于风险偏好型参与者。因此，考虑参与者风险偏好下的利益分配模型将更贴近现实，而本文基于P-DEA效率值修正的Shapley模型则能够比较客观地体现这一点，并将利益在各参与者之间公平分配。

表4 不同风险偏好程度下的效率值和利益分配

5 结论

1) 研究绿色供应链上供应商和制造商为了提高产品绿色度和实现经济利益最大化而组成合作研发平台时的利益分配问题，建立了多家供应商和制造商之间利益分配模型。

2) 利用考虑了参与者风险偏好DEA模型中的效率值重新定义Shapley值中的特征函数，建立考虑参与者风险偏好以及投入、产出重要性和不确定性的修正Shapley值模型，最后通过案例分析验证了模型的可计算性与有效性，得到的利益分配结果与各参与者的贡献程度相吻合，且更贴近实际 情况。

3) 分析不同风险偏好下各参与者的效率值变化情况和DEA有效性，确定了本方法可以为不同风险偏好参与者的利益分配问题提供可行性的决策参考方案，为链上的成员企业提供较为有效的决策判断。

[1] 刘会燕, 戢守峰. 考虑消费者绿色偏好的竞争性供应链的产品选择与定价策略[J]. 管理学报, 2017, 14(3): 451−458. LIU Huiyan, JI Shoufeng. Product selection and pricing strategy of competitive supply chain considering consumer green preference[J]. Chinese Journal of Management, 2017, 14(3): 451−458.

[2] 秦学志, 吴冲锋. 模糊随机风险偏好下的证券投资组合选择方法[J]. 管理科学学报, 2003, 6(4): 73−76. QIN Xuezhi, WU Chongfeng. Fuzzy portfolio selection method under fuzzy random risk preference[J]. Chinese Journal of Management Science, 2003, 6(4): 73−76.

[3] 李勇军, 梁樑. 基于DEA与联盟博弈的固定成本分摊方法[J]. 系统工程理论与实践, 2008, 28(11): 80−84. LI Yongjun, LIANG Liang. A fixed cost allocation method based on DEA and alliance game[J] .Systems Engineering Theory & Practice, 2008, 28(11): 80−84.

[4] 丁乐群, 徐越, 董术涛, 等. 基于AR-DEA联盟博弈的直购电用户转运费用中固定成本综合分摊法[J]. 华北电力大学学报(自然科学版), 2011, 38(1): 60−65. DING Lequn, XU Yue, DONG Shutao, et al. Based on AR-DEA alliance game of direct purchase of electricity users in the transfer cost of fixed cost integrated assessment method[J]. Journal of North China Electric Power University (Natural Science Edition), 2011, 38(1): 60−65.

[5] 李维乾, 解建仓, 李建勋, 等. 基于改进Shapley值解的流域生态补偿额分摊方法[J]. 系统工程理论与实践, 2013, 33(1): 255−261. LI Weijian, XIE Jiancang, LI Jianxun, et al. Method of watershed ecological compensation allocation based on improved Shapley value solution[J]. System Engineering Theory and Practice, 2013, 33(1): 255−261.

[6] YANG Zhihua, ZHANG Qianwei. Resource allocation based on DEAand modifiedShapley value[M]. Elsevier Science Inc, 2015.

[7] 查勇, 宋阿丽, 杨宏林, 等. 考虑决策者风险偏好的机会约束DEA模型[J]. 管理科学学报, 2014, 17(1): 11− 20. ZA Yong, SONG Ali, YANG Honglin, et al. Consider the opportunistic constraint DEA model for decision makers’ risk appetite[J]. Journal of Management Science, 2014, 17(1): 11−20.

[8] 马建华, 艾兴政, 唐小我. 竞争供应链基于下游企业主导的纵向研发联盟研究[J]. 管理学报, 2014, 11(4): 599−604. MA Jianhua, AI Xingzheng, TANG Xiaowo. Competitive supply chain based on the downstream business-led longitudinal R & D alliance research[J]. Journal of Management, 2014, 11(4): 599−604.

[9] ZHA Y, LIANG L. Two-stage cooperation model with input freely distributed among the stages[J]. European Journal of Operational Research, 2010, 205(2): 332−338.

[10] Cooper W W, Deng H, Huang Z, et al. Chance constrained programming approaches to technical inefficiencies in stochastic data envelopment analysis[J]. Journal of the Operational Research Society, 2002, 53(12): 1347−1356.

[11] Kim D J, Ferrin D L, Rao H R. A trust-based consumer decision-making model in electronic commerce: The role of trust, perceived risk and their antecedents[J]. Decision Support Systems, 2008, 44(2): 544−564.

[12] Bauer R A. Consumer behavior as risk taking[M]. Cambridge: Harvard University Press, 1960.

[13] 王晓红, 翟爱梅, 王雪峰. 使用DEA结果修正的多指标综合绩效评价方法[J]. 哈尔滨工业大学学报, 2009, 41(8): 103−106. WANG Xiaohong, ZHAI Aimei, WANG Xuefeng. Multi-index comprehensive performance evaluation method using DEA results correction[J]. Journal of Harbin Institute of Technology, 2009, 41(8): 103−106.

[14] 马士华, 王鹏. 基于Shapley值法的供应链合作伙伴间收益分配机制[J]. 工业工程与理, 2006, 11(4): 43−45, 49. MA Shihua, WANG Peng. Method of revenue distribution among supply chain partners based on Shapley’s value method[J]. Industrial Engineering and Management, 2006, 11(4): 43−45, 49.

[15] Land K C, Lovell C A K, Thore S. Chance-constrained data envelopment analysis[J]. Managerial and Decision Economics, 1993, 14(6): 541−554.

(编辑 阳丽霞)

P-DEA and Shapley value models based on green supply chain profit distribution

LIU Pei, GAO Gengjun

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

Based on DEA model theory of risk appetite and the Shapley value method of alliance game, the P-DEA model was used to correct the Shapley value. According to the member’s relative contribution on the green supply chain system, the interests of the coalition among the participants in a fair distribution mechanism were designed. Finally, the validity of the model was verified by the case analysis. The results show that the Shapley value corrected by P-DEA is more consistent with the relative contribution of the participants by taking into account the risk appetite of the participants and the importance of inputs and outputs, making the distribution results more realistic and maintaining the stability of the supply chain.

green supply chain; P-DEA; Shapley value; profit distribution; union game

10.19713/j.cnki.43−1423/u.2018.09.035

F224；F274

A

1672 − 7029(2018)09 − 2448 − 07

2017−07−05

国家自然科学基金资助项目(71601114)；上海市科委工程中心能力提升项目(14DZ2280200)；上海市科委重点资助项目(12510501600)

高更君(1971−)，男，河南三门峡人，讲师，博士，从事供应链金融与商业运作研究；E−mail：gaogengjun_smu@163.com