基于二次成像的光学图像相位恢复
娄联堂,但 威,陈佳骐,吴高林
(中南民族大学 数学与统计学学院,武汉 430074)
相位恢复(PR)技术是利用已知的强度信息,通过迭代找到最符合真实场强数据的相位分布.相位恢复算法在信号复原、设计光学衍射元件等方面有所应用.迄今为止,已有很多有影响的相位恢复算法. 20世纪70年代Gerchbery和Saxton两位学者提出了有实用意义的迭代相位恢复算法—GS算法[1],即由已知像平面和衍射平面上的强度分布迭代算出相位值.1973年Misell仿照仿照GS算法方案,提出如何由已知两张具有不同离焦量的离焦像来导出波函数的相位值.Fienup于1982年提出了误差减小算法(Error Reduction algorithm, ER)[2]和混合输入输出算法(Hybrid Input-Output, HIO),使得收敛速度大大提高.国内学者杨国桢和顾本源在20世纪90年代提出了一个有效的算法,即杨-顾算法[3-6],这个算法是根据输入和输出两个面上的强度信息计算出输入平面上的相位信息.
本文在杨-顾算法的基础上,提出了一种基于二次成像光学图像相位恢复的新算法.首先通过建立简化的光学成像系统,得到光学图像之间的薛定谔变换[7]关系,然后利用图像薛定谔变换和杨-顾算法来恢复相位.
1 杨-顾算法
杨-顾算法原理[3]简述如下:成像系统中任意的某两平面上的波函数:
U1(x1)=|U1(x1)|ejφ1(x1),
U2(x2)=|U2(x2)|ejφ2(x2),
是通过幺正算符H(H+H=I,幺正算符即H+=H-1)联系起来,即:
U2(x2)=HU1(x1)或|U2(x2)|=
e-jφ2(x2)HU1(x1),
U1(x1)=H-1U2(x2)或
|U1(x1)|=e-jφ1(x1)H-1U2(x2).
杨-顾算法恢复相位,就是要找到这样的φ1和φ2,使得e-jφ2H·[|U1|ejφ1]尽可能的逼近|U2|.用距离D表示二者的逼近程度:
D2=‖|U2|-e-jφ2HU1‖2=
2ReTr[e-jφ1|U1|+HU2]}.
其中|U1|,|U2|表示N维列向量,e-jφ1和e-jφ2表示相位元素组成的N×N对角矩阵,Tr表示矩阵的迹,Re为复数的实数部分.
利用矩阵迹的轮换不变性,相位分布可以通过解下面的变分方程得到,即:
δφ1φ2‖|U2|-e-jφ2HU1‖=0.
解得:
ejφ2=Hejφ1|U1|/abs(Hejφ1|U1|),
(1)
ejφ1=H+ejφ2|U2|/abs(H+ejφ2|U2|),
(2)
已知振幅|U1|和|U2|,可以由(1)、(2)式迭代算出相位φ1和φ2.
2 光学成像系统模型
成像过程的建模是计算机视觉应用的一个重要论题,如移动的结构、物体识别和位姿评估等等.在几何学上,一张照片数据将三维实体空间变成二维图像空间.用于计算机视觉的相机模型一般是立体投影模型,为了重建光学图像的强度测量过程,可以采用一个简化相机模型来实现,如图1所示(与文献[8]中的Figure 10-28类似).图1给出了一个简单的相机模型,相机的光圈置于z=z3平面,光源结合面(z=z5)位于凸透镜镜片的右边,一般来说,相机成像的CCD面(z=z4或z=z6)会在结合面的左边或右边. 用f表示有效焦距 (或简单焦距).用dl表示半径,f满足如下关系:
(3)
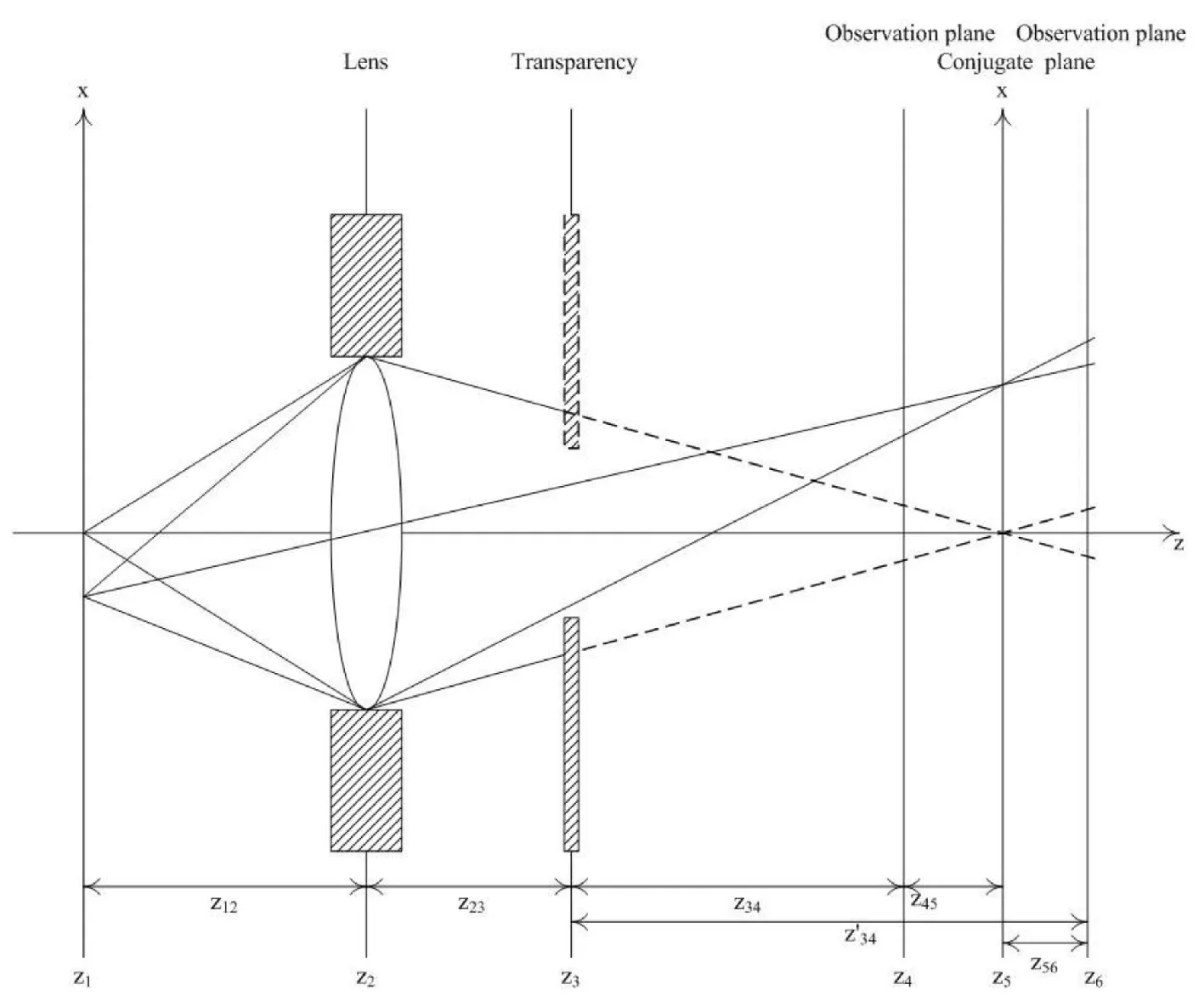
图1 光学成像系统Fig.1 Optical imaging system
由文献[8]可知,相机成像过程中,物体u1(x,y)经过镜片、光圈等的一系列变换处理聚集到CCD上形成密度图像:
u4(x,y)=u1(x,y)**h12(x,y)**
tl(x,y)**h23(x,y)**t3(x,y)**h34(x,y),
其中“**”表示两个二元函数间的二维卷积.对上式作傅里叶变换有:
U4(ξ,η)=U1(ξ,η)H12(ξ,η)Tl(ξ,η)H23(ξ,η)T3(ξ,η)H34(ξ,η),
其中:
H23(ξ,η)=λB23z23jq(ξ,η;-λz23),
H34(ξ,η)=λB34z34jq(ξ,η;-λz34),
那么就有:
其中q(x,y;a)是二次相位信号函数,即q(x,y;a)=eja(x2+y2),q*(x,y;a)为其共轭.q(x,y;a)的傅里叶变换函数是:
(4)
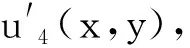
(5)
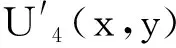
(6)
(6)式涵盖了物距z12、像距z23+z34及焦距f三种变化情况,基本覆盖了大多数光学成像情况.对(6)式作傅里叶逆变换得:
cF-1(ejt(ξ2+η2)F(u4(x,y))),
(7)
其中t为薛定谔变换尺度参数[9].
3 相位恢复算法
3.1 模型的建立
设用同一个相机在手动调焦模式下采用不同的焦距获取的同一目标的两幅图像为|U1(x,y)|和|U2(x,y)|,现在可以假设连续信号分别是空间受限和带宽受限的.图像|U1(x,y)|和|U2(x,y)|的取样点数目均为N=mn,m,n表示图像|U1(x,y)|和|U2(x,y)|的宽和高.利用公式(7)并考虑到数字图像的归一化,那么图像|U1(x,y)|和|U2(x,y)|满足以下关系:
(8)
其中c,d是线性归一化常数(同时考虑到(7)式中的常数c),其作用是修正两次成像得到的图像中心及图像大小的偏移,Ui(x,y)=|Ui(x,y)|ejφi,i=1,2.
根据(8)式以及|U1(x,y)|和|U2(x,y)|来恢复丢失的相位信息φ1(x,y)和φ2(x,y),|U2(x,y)|与c·e-jφ2S(U1(x,y))+d·1的逼近程度,引入“距离”D2来描述,D2的定义[5,6]为:
D2=‖c·|U2|+d·1-e-jφ2F-1e-jt(ξ2+η2)Fejφ1|U1|‖2=‖U3-e-jφ2HU1‖2,
(9)
其中|U1|,|U2|和1都是N维列向量,|U1|,|U2|由图像|U1(x,y)|和|U2(x,y)|的离散数值矩阵拉直成N维列向量.e-jΦ2为N×N对角矩阵,U3=c·|U2|+d·1,F-1,F分别为图像的傅里叶逆变换和正变换的变换矩阵,图像薛定谔变换的变换矩阵H=F-1e-jt(ξ2+η2)F为幺正算符.
3.2 模型求解及恢复算法
由(9)式可得:
(10)
那么相位恢复问题可以转化为求解下列变分方程:
δφ1(D2)=0,δφ2(D2)=0.
而图像归一化的系数c,d则可以由式求导算出.
于是,
ejφ2=Hejφ1|U1|abs(Hejφ1|U1|).
(11)
ejφ1=H+ejφ2U3/abs(H+ejφ2U3).
(12)
c={NRe[Tr(e-jφ2HU1|U2|+)]-
Tr(|U2|1+)Re[Tr(e-jφ2HU11+)]}/
{NTr(|U2||U2|+)-(Tr(|U2|1+))2},
(13)
d={Tr(|U2||U2|+) Re[Tr(e-jφ2HU11+)]-
Tr(|U2|1+)Re[Tr(e-jφ2HU1|U2|+)]}/
{NTr(|U2||U2|+)-(Tr(|U2|1+))2},
(14)
其中abs表示取绝对值,e-jφ1为对角矩阵.
下面给出基于二次成像的光学图像相位恢复的算法步骤:
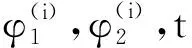
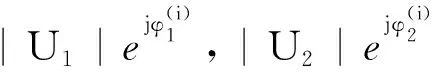

4 实验结果
为了验证新的相位恢复算法,考虑了室内和室外两种情况,相机选用Nikon DX40单反数码相机,实验是在Windows7下使用MATLAB7.10.0下完成的.
采用Nikon DX40单反数码相机(手动调焦模式),通过调节相机焦距对室内水杯进行拍照取样,其ISO曝光度均为100.本文选取了焦距分别为18mm和25mm两张光学图像(图2),经缩小后的图像大小均为581×389.因此,在上述迭代算法中,N的值就是581×389,图2(a)为|U1(x,y)|,图2(b)为|U2(x,y)|,|U1|,|U2|是由581×389矩阵拉直成N=581×389维列向量,而ejφ1,ejφ2为N×N对角矩阵.在实验中,利用图像的薛定谔变换和MATLAB的矩阵点乘来实现相位恢复的快速算法.初始相位φ1,φ2均取为581×389的零矩阵.薛定谔变换尺度参数t设为0.05,误差限ESP设为100(即平均每个像素的误差小于100/N).图3给出了通过恢复的相位重建第二幅图像的过程,随着迭代次数的增加,重建误差越来越小,其中重建误差是根据(9)式计算得到,图3(a)、(b)、(c)的误差ERR分别为49600、9600、100.

(a) f=18 mm (b) f=25 mm图2 室内场景同一目标不同焦距下二次成像Fig.2 Two imaging picture of indoor scene with different focal length

(a) ERR=49600 (b) ERR=9600 (c) ERR=100图3 通过相位恢复重建的图像及重建误差Fig.3 Reconstructed images and errors by phase retrieval
图4(a)、(b)是用同一台相机对室外水杯分别选取焦距为18mm和25mm的二次成像结果,图4(c)是利用图4(a)的灰度、恢复的相位数据及(8)式重建的图像,比较图4(b)、(c)可以看出重建的效果和精度还是比较高的.

(a) f=18mm (b) f=25mm (c) 通过相位重建后的图像图4 室外场景二次成像及通过相位重建后的图像Fig.4 Two imaging pictures of outdoor scene and reconstructed images by phase retrieval
图5给出了图2(a)、(b)及图4(a)、(b)最终相位恢复结果.其中相位图是直接将0到2π范围内的相位角归一化到0~255来实现的,因此会出现一定的误差.从相位图中能大致看出杯子、凳子及背景分界线的形状,因此表明恢复的相位图有一定的可信度.

(a)图2(a)相位图 (b)图2(b)相位图 (c)图4(a)相位图 (d)图4(b)相位图 图5 相位恢复结果Fig.5 Results of phase retrieval
实验中,为了不分散对算法的注意力,文中假设薛定谔变换尺度参数t为某一固定值(实验中取为0.05),从恢复图像以及得到的相位图像可以看出恢复的效果比较好.但在实际中,这个参数是不确定的,它与相机成像模型参数有关,如何求出参数t,将是下一步工作的重点之一.

