一种基于RBF自适应神经模糊推理的短期电力负荷预测方法

王晓侃 王 琼

(1 北京交通大学 电子信息工程学院，北京 100044；2 河南机电职业学院，新郑 451191)

电力系统负荷预测是实现电力系统安全、经济运行的基础.对一个电力系统而言，提高电网运行的安全性和经济性，改善电能质量，都依赖于准确的负荷预测.电力系统在逐步发展、完善过程中，负荷预测己成为能量管理系统(EMS)中一项独立的内容，在当前电力系统市场化的必然趋势下，负荷预测己成为电力市场交易管理系统中必不可少的一部分.在实际应用中，电力系统不同组成部分对负荷预测的范围和精度有所不同，因此研究负荷变化的内在规律和负荷特性、影响负荷变化的各种相关因素以及各种相关因素在预测如何进行规范化处理对提高预测精度及负荷预测的发展有重要的意义[1-3].

1 基于RBF自适应神经模糊推理(ANFIS)方法

基于RBF的ANFIS是通过采用神经网络来达到模糊推理的目的[4,5]，模糊控制的三个最基本的过程，即模糊化、模糊推理和反模糊化这三个过程都是通过神经网络来实现的.神经网络的自主学习机制可以对输入其中的数据进行抽取，模糊系统能够轻松表达人类的知识，还可以弥补传统的模糊控制的不足，无需反复对模糊控制器的中心函数进行调整，就可以缩减误差，提高效率.

通过学习混合算法，按照人类的认知和特定的输入/输出数据对建立起一个输入/输出映射[6-8].

1.1 基于RBF的ANFIS结构描述

Sugeno模糊模型有一条非常典型的推理规则：ifxisAandyisBthenz=f(x,y).规则中：A和B可以看做模糊数的前提，z=f(x,y)是推理结果中的精确数据.f(x,y)是x和y的多项式.相对应的，Roger Jang提出了一套自适应神经网络模糊推理系统，该系统可以达到学习Sugeno模糊模型的功能，其功能等同于一阶Sugeno模糊模型，可以看作是该模糊模型的一种神经网络再现模式.ANFIS的网络结构式多层前馈型的，具体如图1所示[8].

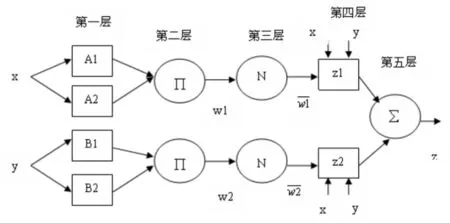
图1 ANFIS结构图Fig.1 Structure of ANFIS

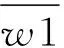
从图中给出的信息可以看出来，ANFIS模型的结构主要分为：对模糊隶属度进行测算，找到每一条规则的适用度，对适用度进行规划合一，计算每条规则的输出，模糊系统的整体输出数据有五个层次，数据经由输入层输送到下一个层级，模糊化层级的输出数据是一个与模糊推理中的模糊状态相对应的隶属函数，模糊推理层由模糊推理的前提和得出的结论两方面构成.反模糊化层则给出一个明确的输出让整个系统以此执行相关任务，通过对给定的数据样本能够灵活的调整不同层级之间的连接权系数值，能够让系统反馈的结果更贴近实际的反应真实的系统模型.以下是它的网络结构[8]：

第一层是模糊化层；主要负责对输入的数据进行模糊化处理，节点i的输出函数如下：

(1)

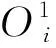
(2)

在(2)式中{αi，βi，γi}作为前提参数，αi是宽度，βi是斜率，γi是中心位置，对这些参数进行调整，就会让隶属函数的形状发生变化；公式中的隶属函数可以随意分段成连续函数，比如用梯形函数或者高斯函数等都可以.

第二层是规则的释放强度层；该层的节点主要作用是把输入的信号进行相乘处理.例如：

wi=μAi(x)×μBi(y),i=1,2.

(3)

上面每一个节点的输出显示了这条规则的可信度，任何满足T规范的AND算子都可以作为这里的 “×”.这个公式项目的运算结果就明确了不同的模糊规则激活的强度.

在第三层所有的规则强度规划为一.第i个节点上的第i条规则经过归一化处理之后的可信度计算公式如下：

(4)

该层每个节点均为圆节点(固定节点)，计算模糊规则的权系数，对模糊规则的激活强度.

第四层主要负责输出模糊规则.计算不同模糊规则的输出结果数据，公式中每一个节点都对应着一个自适应节点，其中第i个节点的输出数据计算如下:

(5)

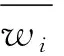
第五层是解模糊层，在这一层立只有一个节点，它代表的是所有的输入信号的总和，也就是这一次推理过程得到的结论：

(6)

因此，在给出了特定的隶属函数之后， ANFIS最后的输出数据也就是结论可以表示为各种结论参数的线性组合：

(7)

以上组合推论可得，对于拥有m个输入变量且每个输入变量有k个模糊集的Sugeno模糊模型，是可以通过上面介绍的方法来转化为神经网络结构的，这种控制规则的总数值为n=km.

1.2 基于RBF的ANFIS学习算法

通过神经学习技术来操纵神经模拟控制器可以灵活调整神经模糊控制系统的各种参数和结构.对神经模糊控制器的调节主要有两种类型，一是结构调整，二是数据调整.对结构的调整主要包括对变量的数目、规则的数目和输入输出的变量论域划分的调整；在调整效果满意之后，就需要对参数进行相关的调整了参数的调整主要包括：与隶属函数有关的参数(中心、宽度、斜率)等进行调整.在特定的网络结构下，这种学习方法更多的是对控制器的参数进行学习和调整，即对前提参数和结论参数进行调整.

学习法主要是采用最小二乘和梯度下降结合的混合算法；这种算法综合了两种算法来辨别参数，对前提参数使用梯度下降法，对结论参数使用最小二乘法；这个学习过程包含了前向学习和反向学习两部分.前向学习主要包括了ANFIS的前四层学习，这四层的结论参数都是经过最小二乘算法求得的.而反向学习梯度下降法，在固定输出参数不变的前提下，通过对输入层和其他中间层的参数进行优化调整达到降低误差的目的.通过控制和掌握返回误差的变化率灵活调整前提参数{αi,βi,γi,}优化调整隶属函数的形状，让整个样本数据的均方差数据符合规定的精准度要求.

2 电力负荷预测结果及分析

短期负荷预测的一个突出特点是：为对系统负荷进行预测，必须对过去的负荷历史资料进行分析.因为电力系统的负荷本质上是不可控的，了解未来短期内的负荷的可能变化的一个最有效的办法就是观察和分析负荷的历史记录数据.因此要充分考量负荷变化受到周期性影响和天气因素影响的原因及规律，找到负荷受影响及变化的规律特性，根据得出的结论应用基于RBF自适应神经模糊推理的方法来预测未来的短期时间内负荷数据和走向，并应用MATLAB进行预测仿真[9].

2.1 负荷预测时神经网络隐含层节点的确定

本文的预测模型采取的是基于RBF自适应神经模糊推理模型，该模型综合分析了负荷的特点，按照日期类型分为四类：周一，工作日(周二到周五)，周六，周日.每一个类型都是要全天对24个小时进行日负荷预测，因此四个日期类型总共建立了96个神经网络模型.在这个神经网络模型中我们一共设置了96个输入节点，每一节点采用的时间不同，分别设定在预测日前一天、前两天、前一周的相同时刻；此外还包括预测日及前一天的前一个时刻和前两个时刻的负荷数据；预测日及其前一天的温度情况，包括最低温和最高温，预测日当天的天气情况数据，包括天气情况度量值和预测日当天的日期类型变量数据；96个输入节点对应一个输出节点，也就是预测日的整点负荷值.由此可知，文中涉及到的隐含层的数目是通过实验的方法取得的；随机地对某个地区的电网进行了全天24小时的预测，预测数据和实际误差结果对照如下图2所示.

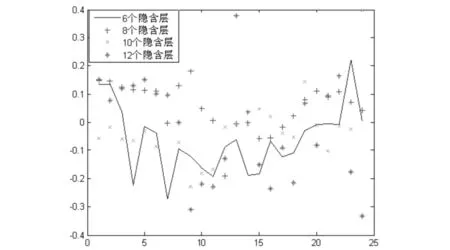
图2 隐层神经元数目不同的预测误差曲线图Fig.2 Hidden layer neurons in the number of different forecasting error curves

由图2可见，隐层神经元的数目不同，预测的结果和实际对照的误差都会不同，对比发现，当隐层神经元数为8时，预测结果和对照实际数据的误差平均值最小，也就是最符合实际结果.这样的实验对比结果还有很多，综合来看，当隐层神经元为8时，取得的预测效果最贴近实际观察结果.所以，本文确定隐层神经元数目为8.

2.2 负荷预测方法的比较

综合采用RBF网络神经算法、BP神经网络算法和基于RBF自适应神经模糊推理三种方法对东莞电网2017年01月08日的负荷数据进行预测，三种预测方法得出的结果和实际的观察负荷结果进行对比的结果如表1和图3所示.

表1 不同预测方法的预测结果比较

Tab.1 Forecasting results comparisonbased on different forecasting techniques

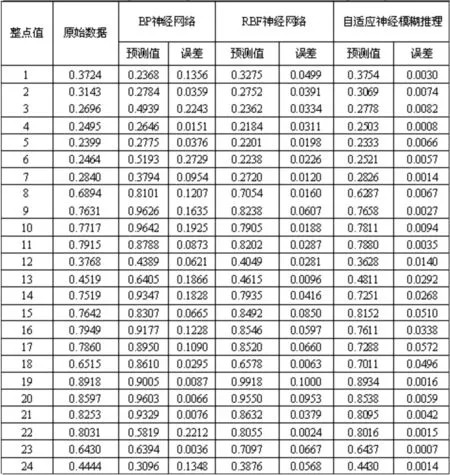
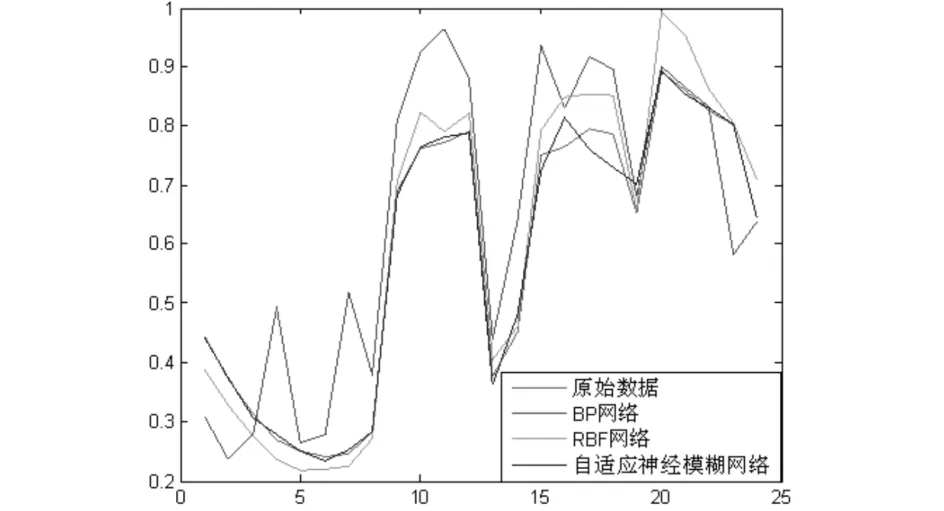
图3 BP神经网络算法、RBF神经网络算法和RBF自适应神经模糊控制算法预测结果曲线图Fig.3 Bp and RBF Neural Networks Algorithm and RBF ANFIS forecasting curves

由表1可以看出，BP神经网络的预测误差最大值为0.2729，RBF神经网络的预测误差最大值为0.1，RBF自适应神经模糊控制的预测误差最大值为0.0572，可见其RBF自适应神经模糊控制的相对误差最小，证明了自适应神经模糊控制有效地提高了负荷预测的精度，达到了实际运行的需要.

从图3中可以看出，RBF自适应神经模糊控制的逼近能力最好.这表明RBF自适应神经模糊控制能很好地进行电力负荷的预测.

3 结语

基于RBF自适应神经模糊推理方法具有收敛速度快，拟合能力强，预测精度高，训练结果惟一等优点，将其应用于东莞地区的短期电力负荷预测，用MATLAB编程仿真，结果表明基于RBF自适应神经模糊推理的短期电力负荷预测结果与实际情况比较吻合，取得了满意的效果.