利用磁光克尔效应计算材料的介电张量非对角元

曹 克，张 霞，王玉颖，孙学博，孔祥和

(曲阜师范大学 物理工程学院 山东省激光偏光信息重点实验室，山东 曲阜 273165)

磁光器件是光通信中的重要元器件[1]. 为满足光通信的发展要求，器件体积微型化、信息密集化、响应灵敏化以及实现全光控制是研究的重点[2]. 为此，针对上述需求，人们对基于各种物理机理、具有以上性能的磁光材料进行了详细地研究[3-6]. 而在对这些材料的研究和应用过程中，对材料的光学性能表征既是应用的前提，也是进一步改善材料性能的关键. 利用椭偏仪可以对材料的光学性能进行分析，从而得到介电张量的对角元部分[7-9]. 对于介电张量的非对角元，并不能单纯地依靠椭偏光谱表征得到[10-12]. 而这些材料的宏观特征量中，非对角元张量是非常重要的参量，体现了磁光材料或其他微结构材料的非互异性性能[13-17]. 光通信中对非互易性器件的需求，要求材料科学工作者不断探究新型具有非互易性的材料. 因此，对材料非对角元准确地表征，是研究光通信中非互易性器件的关键.

磁光克尔效应不仅可以用来表征磁光器件的性能，而且还可以用来研究材料的物理性质[18]. 磁光克尔效应是指线偏振光束入射到被磁化的物质上时，光的左右旋态退简并，由于左旋光和右旋光的光学常量不同，使得光经过磁化物质反射以后，光的偏振态会发生变化. 磁光克尔效应是探测光的偏振变化的手段，具有极高的灵敏度. 材料的磁光克尔效应是其内在禀性的宏观体现，其大小决定于物质的介电张量的对角元和非对角元. 因此，结合椭偏测量，通过磁光克尔的测试分析可以表征材料介电张量的非对角元. 本文通过磁光的理论分析，结合磁光参量和光学参量，推导出磁光介电张量非对角元的计算公式，并用电化学制备的样品测量分析进行验证.

1 基本原理

根据样品表面、磁场方向及入射面三者的关系，磁光克尔效应可分为横向克尔、纵向克尔和极向克尔效应. 在这里，以极向克尔效应为例，也就是当磁场的方向垂直于样品表面，平行于入射面时. 在这种情况下，当1束线偏振的光入射到固体表面时，反射光变为椭偏光，并且偏振面会发生微小的旋转，用旋转角θk和椭偏率εk来描述材料的磁光克尔效应.

在笛卡尔坐标中，设样品的表面位于xy面内，磁场沿z轴方向时，电介质函数张量为[18-19]复折射率可用介电张量表示为[18]

(1)

(2a)

(2b)

(3)

利用复折射率和介电张量之间的关系式(2a)和(2b)及电介质材料的性质，设εxx≫εxy[18]，得[20]

(4)

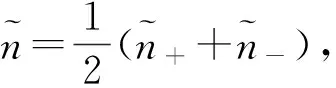
(5a)

(5b)

其中系数为

A=n3-3nk2-n,

(6a)

B=-k3+3n2k-k.

(6b)

由式(5)和(6)得介电张量非对角元为

εxy1=Aθk-Bεk,

(7a)

εxy2=Bθk+Aεk.

(7b)

2 样品制备与测试结果分析

采用磁控溅射法制备样品，靶材购于北京中金研新材料科技有限公司，Ag纯度为99.999%，Cr纯度为99.95%，Co纯度为99.99%，溅射过程中使用的Ar气纯度为99.999%. 计算软件采用Matlab. 测量设备采用法国Jobin Yvon公司的EX-SITU UVISEL型椭偏仪，其光谱有效范围250～830 nm，近红外延伸到2.1 μm,紫外可扩展到190 nm.

Co-Ag薄膜样品生长在玻璃衬底上. 首先，在清洗干净的载玻片上利用直流磁控溅射的方法先溅射Cr(20 nm)作为缓冲层，目的是增强贵重金属的附着性. 然后原位溅射Ag薄膜(200 nm)，溅射气压为0.30 Pa，溅射功率为30 W. 200 nm远远超出Ag的趋肤深度[21]，这样保证在测试光学性能时没有Cr的影响. 最后原位溅射Co薄膜，生长完毕后等待约1 h取出薄膜样品. 溅射时本底真空为5×10-5Pa，工作气压为Ar气压0.35 Pa，溅射功率为35 W. 通过改变溅射时间，制备了Co薄膜厚度分别约为10 nm和20 nm的样品. 为比较，制备了纯厚度为200 nm的Ag薄膜样品.

样品的椭偏光谱测试波长为300～800 nm. 在自行搭建的光谱测试系统上进行磁光克尔测试，测试中，采用极向磁光克尔效应，室温25 ℃，外加磁场为1 T，方向垂直于样品表面，测试波长为300 ～800 nm.

图1是磁光克尔测试结果，图2是椭偏测试拟合折射率和吸收系数测试结果.

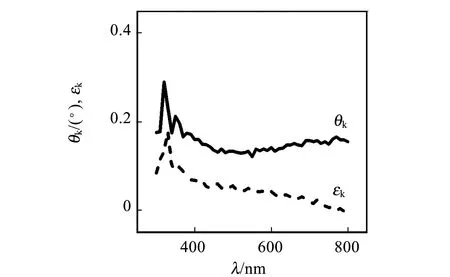
(b)Co(10 nm)/Ag

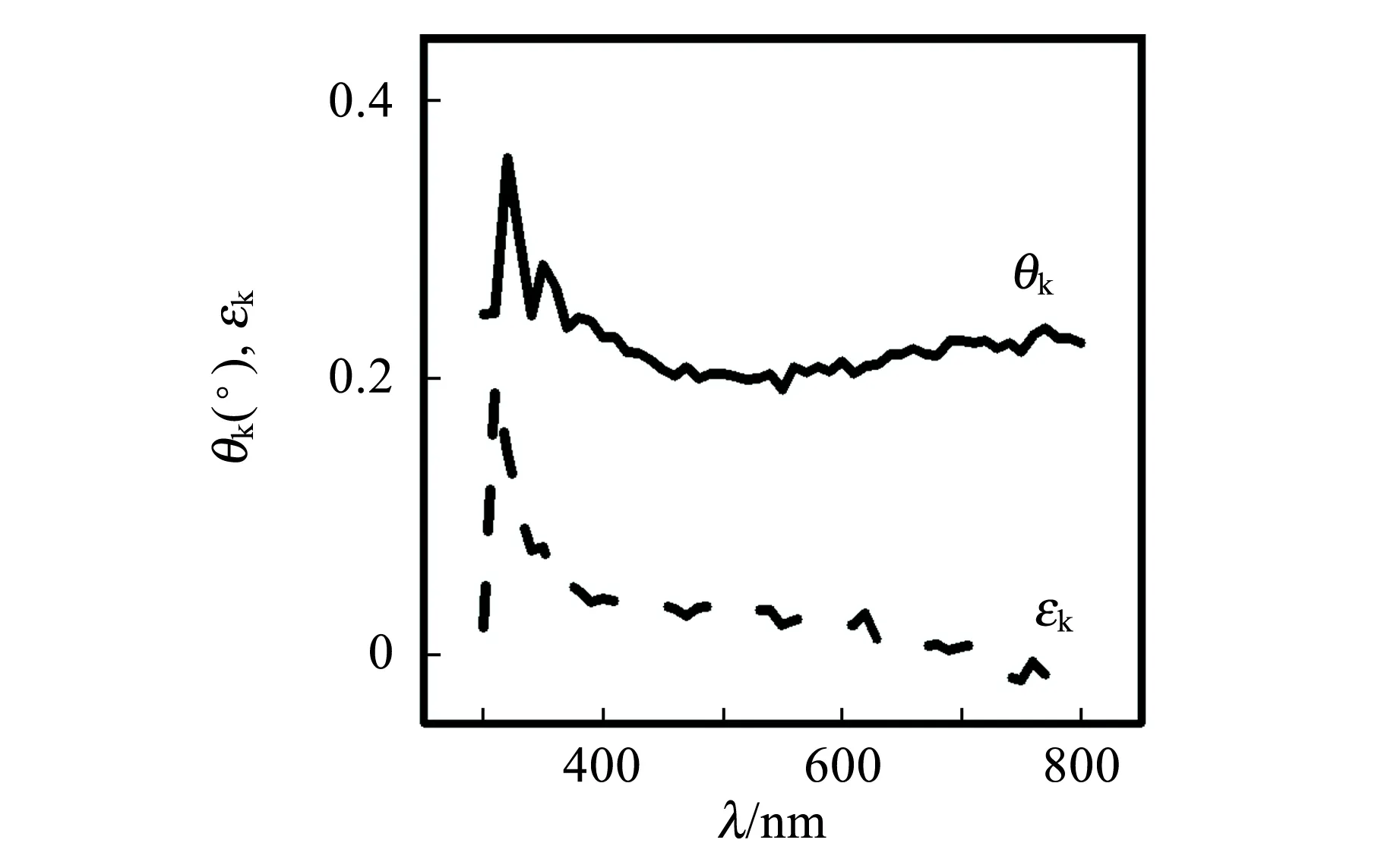
(c)Co(20 nm)/Ag图1 磁光克尔测量结果

(a)Ag

(b)Co(10 nm)/Ag

(c)Co(20 nm)/Ag图2 椭偏测试拟合折射率和吸收系数结果

从图1～2中可以看出，Ag薄膜的磁光克尔转角和椭偏率在光学常量的共振跃迁位置处有1个特征谱，克尔椭偏率呈现很窄的峰，而克尔转角比较宽而平. 对于Co/Ag双层薄膜，无论是Co为10 nm还是20 nm，磁光克尔都在λ≈315 nm附近有1个特征谱峰结构，并且克尔转角是Ag薄膜的5倍左右，单纯Co薄膜材料的克尔谱在λ≈315 nm并没有特征结构，因此推断，Co/Ag双层薄膜在λ≈315 nm处的特征结构来自界面上的等离子体共振吸收. 比较其光学常量测量结果,在λ=315 nm处没有明显的特征结构. 这说明磁光测量方法具有极高的灵敏度.

3 介电张量非对角元计算

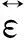
(a)基于磁光与椭偏参量计算结果

(b)椭偏参量拟合计算结果图3 Ag薄膜介电张量的对角元

可以看出，2种方法计算出的介电张量对角元的值基本一致，在λ≈315 nm处都有1个特征结构. 这表明在纯Ag的非磁性金属薄膜中，由式(5)～(7)计算得到的Ag薄膜介电张量对角元的可行性. 图4是由式(5)～(7)计算得到的Ag薄膜介电张量非对角元的实部和虚部. 相比其对角元张量，非对角元张量比较小，除在λ≈315 nm有1个特征结构外，其余部分相对平坦. 低频处的峰-谷结构来自于振荡.

图4 纯Ag的介电张量非对角元计算结果

上述Ag薄膜计算的结果验证了计算方法的可行性. 在此基础上，进一步来分析含磁性贵金属材料Co/Ag双层薄膜非对角元的计算. 图5是由式(5)～(7)计算得到的Co/Ag双层薄膜介电张量对角元(a,b)和非对角元(c,d)的实部和虚部. 可以看出，磁性材料的厚度对介电张量影响不大. 介电张量对角元的实部和虚部分别随波长单调递增和递减，并且其光谱中没有任何的特征结构. 但是对于介电张量的非对角元，除了呈现变化的趋势外，在λ≈315 nm处，有1个比较弱的特征结构，对应于磁光信号中在λ≈315 nm处的特征结构.

(a)厚度10 nm的对角元实部和虚部

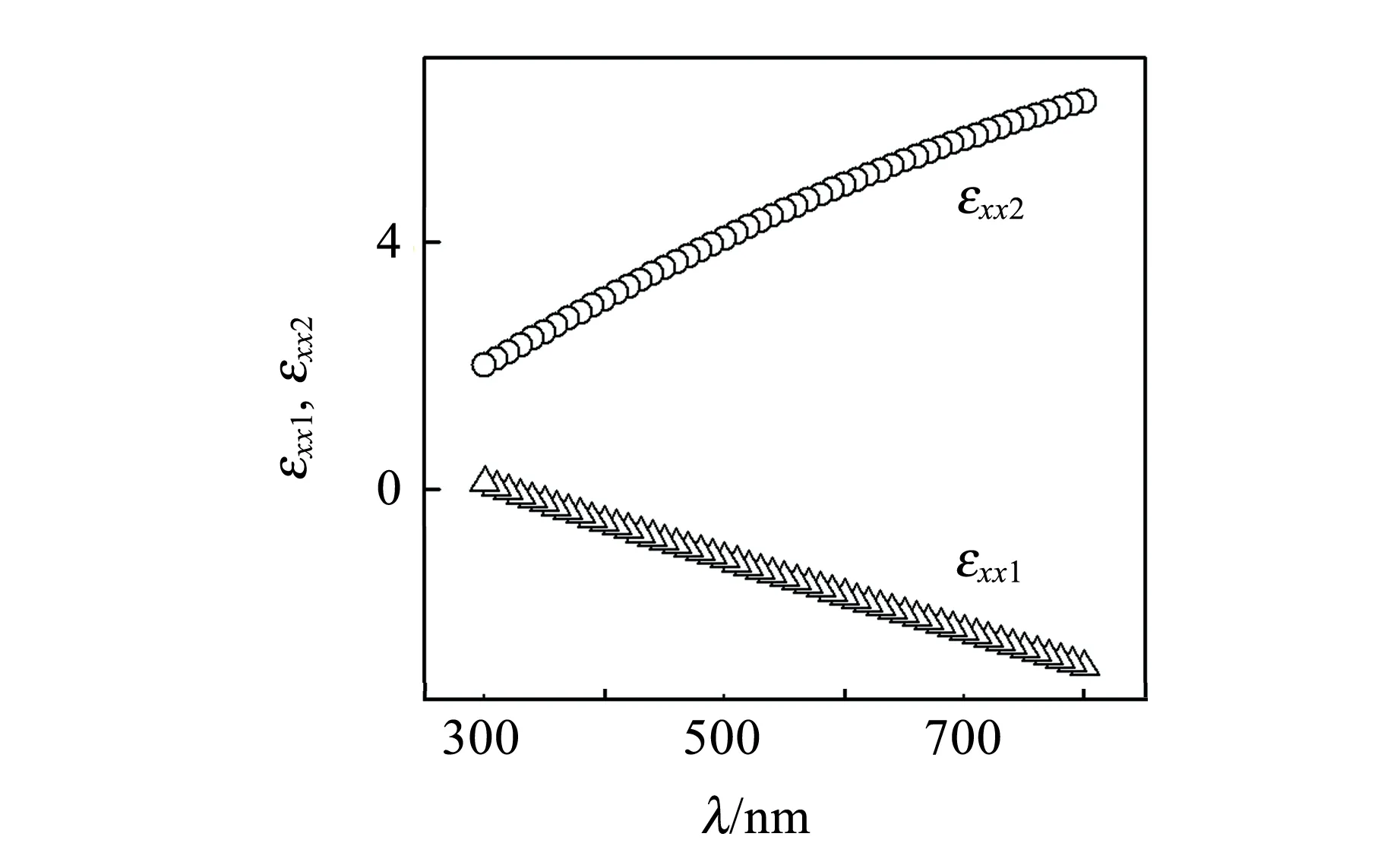
(b)厚度20 nm的对角元实部和虚部

(c)厚度10 nm的非对角元实部和虚部

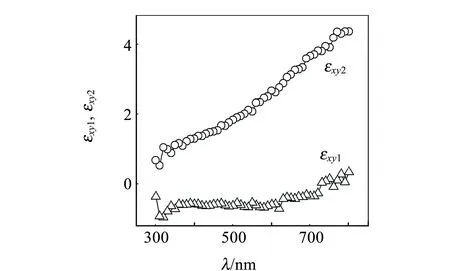
(d)厚度20 nm的非对角元实部和虚部图5 Co/Ag薄膜不同膜厚的对角元与 非对角元的实部和虚部

4 结 论

通过理论分析推导出利用磁光克尔效应计算介电张量的非对角元的方法，并通过对磁控溅射生长的Ag以及Co/Ag薄膜的磁光克尔测试和椭偏测试分析，利用推导得到的公式计算了Co/Ag双层薄膜材料介电张量的非对角元. 通过磁光信号、椭偏测量拟合得到的光学常量以及计算得到的介电张量的对角元和非对角元对比分析可知，对于非磁性介质Ag，其磁光克尔效应主要是克尔椭偏率的变化，其来源为对角元与非对角元的共同贡献；而对于含磁性/贵金属混合体系，Co/Ag双层薄膜测试分析的结果说明，磁光克尔的来源主要是磁性材料，但是强度上贵重金属的等离子体吸收边起到很大作用，且磁光的特征结构发生在贵重金属的等离子体吸收边位置处. 采用2种不同方法计算Ag薄膜介电质张量的对角元，得到基本一致的结果，利用磁光与椭偏测量得到的数据计算介电张量的非对角元，从而保证了用这种方法来计算含贵重金属和磁性材料混合薄膜体系中的介电质张量非对角元是可行的.