系数矩阵中部分有界不确定性的混合平差算法

王志忠，宋迎春，何玲莉

1. 中南大学数学与统计学院，湖南 长沙 410083； 2. 中南大学地球信息科学与物理学院，湖南 长沙 410083

在测绘数据获取过程中，不可避免的误差来源使观测数据与真值间存在差异，人们认为数据具有不确定性，其实质是指数据的误差[1]。不确定性是不精确性、模糊性、不明确性等概念的一个总称，它与误差的意义相近。但前者指一种广义的误差，它包含可度量的数值误差和难以度量的概念误差。很多时候测量数据的不确定性不再是一个具体数值，它们可能各自在一定的实数区间内变动，或者仅是一个模糊数，此时沿用随机误差的分布限定会使测量平差数据处理效果受到影响[2]。为抑制观测不确定性因素的影响，很多学者做了相关的研究。如运用整体平差算法[3-5]来进行数据处理，它总体上考虑了观测向量L和系数矩阵A的误差，但容易出现对A的过度校正，从而影响状态参数估计的可靠性。后有文献[6]提出给这种校正加上先验上界。后续研究包括应用不确定度理论研究不确定性评定方法[7-11]，寻找抑制不确定性影响的算法[8，12-13]，针对不确定性建立新的平差准则[14]等。

不确定度是不确定性的一种度量指标体系，它与测量界的精度度量方式几乎一致，所有不确定度均可以用方差、均方差、误差区间、误差椭圆、误差椭球表示[15]。在测绘数据处理领域，应用先验信息和不确定度理论进行抑制观测不确定性影响的相关研究已成为热点。文献[2]、[6]和[14]直接将不确定度作为一个参数融入函数模型中，建立不确定性平差模型，依据不确定性min-max平差准则，利用奇异值分解，而后迭代求解该问题。文献[16]针对不确定性min-max平差准则等价转换后的形式，提出了一种可行的加权方法，增加了参数估计的可靠性。文献[17]将文献[6]提出的不确定性度量方法融入不确定性平差模型中，并给出了新的参数求解算法。

本文在文献[17]方法的基础上，将随机误差和有界不确定性误差平方和最小的新平差准则运用到不确定性混合平差模型求解中，提出了一种新的迭代求解算法，并证明了该算法的收敛性，简化了文献[2，14]中的算法，同时其应用范围更广。

1 系数矩阵中部分有界不确定性的混合平差模型

建立如下不确定性混合平差模型

(1)

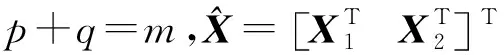
关于平差模型的误差设立，文献[18]研究的污染误差模型仅考虑模型误差和随机误差，未对模型误差作约束。文献[19]研究的总体平差模型考虑了随机误差和系数矩阵误差，未对系数矩阵误差作约束。文献[2]在文献[14]的基础上引入了观测变量和系数矩阵的有界不确定性误差，但未考虑随机误差。文献[17]在文献[2]的基础上考虑了随机误差，也做了不确定性误差有界约束。在测量实践中，会遇到方程式系数矩阵部分有误差的情况，诸如曲面拟合、GPS伪距单点定位、坐标转换模型等[20]。因此，本文将系数矩阵A分割为A1和A2，提出不确定性平差模型(1)。

模型(1)中的不确定性误差的有界性约束可看成是A2和L的先验信息[2]。文献[2]对所建立的平差模型采用的min-max准则进行参数解算，但该准则无法利用观测信息和先验有界信息估计不确定误差ΔL和ΔA2。另外，未知参数X的估计结果中不含不确定度β，这导致不确定性误差ΔL对平差解算结果没有影响。鉴于此，本文基于模型式(1)，在式(1)的不确定性误差有界约束下，提出了随机误差和不确定性误差平方和最小准则

(2)

关于带约束的最小二乘问题，文献[21]提出了一种线性不等式约束平差模型算法，文献[22—24]针对总体最小二乘模型中附加等式约束给出了Euler-Lagrange逼近解算方法。对上述参数带有约束的最小二乘问题，本文参照前述文献的方法，引入Lagrange乘子，结合Kuhn-Tucker条件求得参数最小二乘估计的一般形式。

根据Euler-Lagrange求极值方法，构造如下目标函数

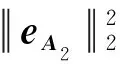
(3)

式中，λ1为n×1维Lagrange乘子；λ2、λ3为1×1维Lagrange乘子，均非负。运用Kuhn-Tucker条件得到

(4)

其中，⊗表示Kronecker积。由式(4)可得

(5)

(6)

(7)

将式(6)代入式(7)得

(8)

(9)

将式(6)代入式(4)得

(10)

将式(6)代入式(4)得

(11)

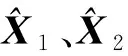
(1)λ2>0，λ3>0。据式(4)可知

(12)

将式(10)和式(11)代入式(12)解方程组得到

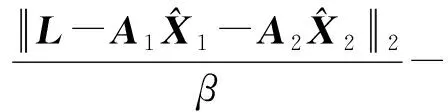
(13)

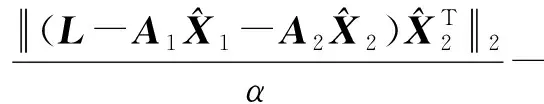
(14)

将式(13)和式(14)代入式(10)和式(11)即得不确定性ΔL和ΔA2。

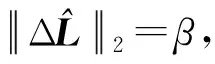
(15)

故而不确定性可分别表示为

(16)

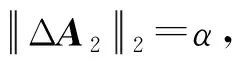
(17)

从而不确定性可以表示为

(18)

(4)λ2=λ3=0(λ2<0视为λ2=0，λ3<0视为λ3=0)。此时，不确定性分别为

(19)

利用式(9)求解X1和X2非常复杂，考虑用迭代法求解。下面讨论迭代过程的收敛性问题。

由式(9)得

(20)

(21)

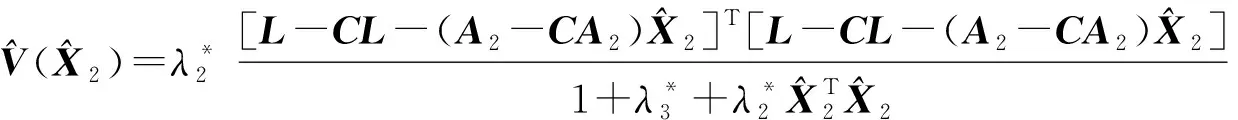
(22)

其中，

(23)

利用式(4)和式(5)，式(21)可简化为

(24)

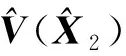
(25)

(26)

(27)

该算法收敛。

在上述不确定性混合平差模型中，若令α→+，β=0。则根据式(4)可知λ2=0，如此对应于Lagrange乘子分类讨论的情况(2)，则由式(15)可得λ3=+，从而将之代入式(8)得到

(28)

此与文献[23]中公式一致，即混合总体最小二乘模型。因此，本文的不确定性混合平差模型可认为是更广的混合平差模型。

2 不确定性混合平差模型解算方法

根据上述推导可归纳迭代计算步骤如下：

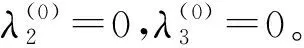
X0=(ATA)-1ATL，其中A=[A1A2]，

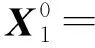
其中，E1、E2分别为对应维度的单位阵。

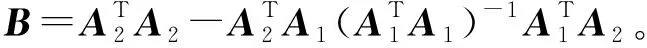
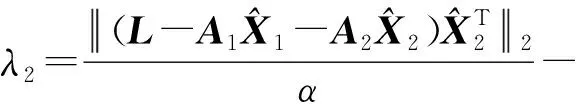
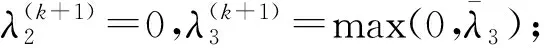
3 不确定性混合平差模型解算与分析

在应用包括GPS在内的空间定位技术进行测量时,往往还需要进行不同基准间的转换。进行基准转换的模型很多,较为常用的有布尔沙-沃尔夫(Bursa-Wolf)模型和莫洛金斯基(Molodensky)模型[25]。本文将文献[25]中的Bursa-Wolf模型改写为不确定性混合平差模型。基于空间坐标采样数据，分析比较了该模型min-max准则下的算法(ULS1)和本文提出的算法(ULS2)的解算优劣。数据见表1。该数据共19个观测点，57条数据。其中前16个观测点用于建立转换模型，并进行参数估计，后3个观测点用于预测和比较。

表1 原始空间坐标数据

对文献[25]中的Bursa-Wolf模型进行适当变形得到

(29)

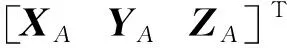
则有

L=A1X1+A2X2

(30)

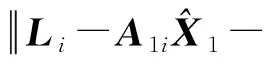
表2 ULS模型估计性能与不确定度的关系

表3 2种算法预测精度比较(δ=0.000 1)

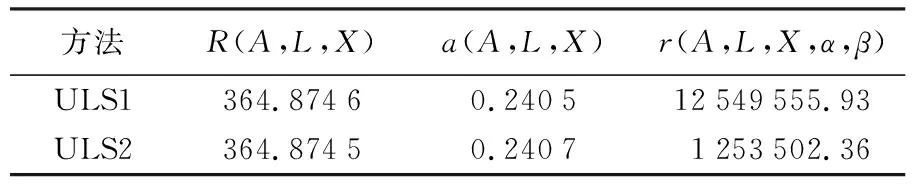
表4 算法解在不同目标函数下的取值(δ=0.000 1)

在实际情况中，由于模型误差、人为误差、仪器误差以及样本影响等，同一控制点在两套坐标系下的坐标量测值均包含了误差，这使得观测向量L和系数矩阵A2都需要修正。本文运用混合不确定性模型来解决该数据误差问题，最终使得新旧坐标系下的坐标测量值都能够平等、匀称地进行改正。

4 结 论

目前的测量平差理论大多是基于“观测值的不确定性就是随机性”的假设进行的研究。但在实际测量工程中，有许多不确定因素是不同于传统的随机性误差的，它们没有分布规律，因而无法进行统计描述。所以有文献将观测中的不确定性因素进行数值化、参数化后融入平差模型中。本文沿用以上思路，提出了基于混合不确定性模型的参数求解算法。主要有以下结论：

(1) 结合部分系数矩阵A2和观测向量L存在一定的误差的事实，本文将平差模型扩展到混合不确定性平差模型，该模型在某些应用领域更加切合实际。

(2) 本文将不确定信息转化为先验信息，以参数的形式融入模型，建立有界不确定性约束下随机误差和不确定性误差平方和最小的平差准则，最后对该优化问题进行迭代求解。从参数估计的残差角度考虑，min-max准则下的算法所得残差取值几乎总是大于本文算法，说明本文所提算法精度更高。

(3) 本文算法利用了有界不确定性误差的先验信息-不确定度β，而文献[2]的参数估计结果中没有β，这样的结果未体现不确定度β作为参数融入模型的意义。

(4) 在本文算例中，当不确定性设定在一定范围内时，本文所提算法所得结果变化不太大。说明在坐标转换中，转换参数对系数矩阵的有界不确定性误差不十分敏感，也有可能是测量不确定性过大淹没了矩阵的有界不确定性。