基于等效电气距离的强迫功率振荡时空传播特性分析

陈 凡，黄少雄，丁津津，郭 力，邓倩倩

(1.国网安徽省电力有限公司电力科学研究院，安徽 合肥 230601；2.国网安徽省电力有限公司电力调度控制中心，安徽 合肥 230022)

0 引言

强迫振荡理论是区别于负阻尼机理的另一经典理论，其成功地解释了系统阻尼足够大的情形下发生的低频振荡问题，正在引起业界越来越多的关注[1,2]。该理论指出，当系统遭受持续的周期性功率扰动且扰动频率接近系统的固有频率时，会激发系统发生大幅度的功率振荡。强迫振荡具有起振快、起振后会持续等幅振荡、扰动源消除后振荡很快衰减的特点。

强迫功率振荡的研究起步较晚，学术界的研究主要集中在振荡机理研究、扰动源定位技术研究以及振荡抑制技术研究这几个方面。在振荡机理研究方面，学者们已经从解析法、状态空间法、复模态分析等手段开展了研究，推导了单机无穷大系统、多机系统的强迫功率振荡机理，也研究了负荷周期性扰动诱发强迫功率振荡机理[1～3]。在扰动源定位技术方面，目前思路主要有能量法、行波法以及其它方法。文献[4]通过研究扰动过程中不同的能量变化特性来达到定位扰动源的目的，文献[5]对多个监测单元电压信号波形进行相似度比较，利用扰动行波在电网输电线路上的传播延时时间进行定位，文献[6]根据扰动机电波传播到不同位置的时刻具有时间延迟的特点，提出一种利用最小均方时延估计法定位扰动源的方法。在振荡抑制技术方面，研究表明最有效的方式是准确定位并切除扰动源，使强迫功率振荡能够快速平息，其次通过对PSS参数进行优化，增加系统的阻尼，使其兼具抑制负阻尼低频振荡和强迫功率振荡的作用。

为了更好研究强迫振荡的扰动源定位和抑制技术，有必要对强迫振荡扰动波时空传播特性进行研究，以期找出振荡发生后扰动机电波传播到系统各节点的时间先后规律。本文基于等效电气距离理论，分析了电网发生强迫功率振荡时的时空传播特性，指出离强迫振荡扰动源的等效电气距离越近的节点，频率变化量扰动机电波越先到达，反之亦然。最后利用PSD-BPA软件对WSCC 3机9节点算例进行仿真分析，结果证明了上述结论的正确性。

1 强迫功率振荡机理

在单机无穷大系统中，发电机采用经典二阶模型，参考机械振动学理论，采用解析法分析强迫振荡的机理[1]。假设扰动发生在原动机侧，将发电机运动方程在工作点处线性化得到：

(1)

考虑到ΔPm=F0sin(ωt)，ΔPe=KSΔδ，代入上式有：

(2)

式中：ΔPm为机械功率扰动，ΔPe为电磁功率扰动，TJ为发电机惯性时间常数，ω0为系统基准角频率，δ为发电机功角，D为发电机阻尼系数，KS为发电机同步转矩系数，F0为扰动幅值，ω为扰动角频率。

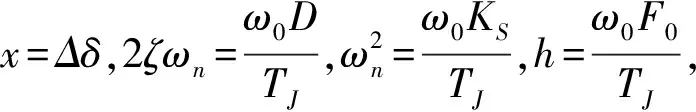
(3)

对式(3)所示的二阶非齐次微分方程求解，得到：

x(t)=e-ζωnt[B1cos(ωdt)+B2sin(ωdt)]+Bsin(ωt-φ)

(4)

(5)

式(4)中等号右边第一项表示由扰动引起的自由振荡，在系统阻尼作用下将衰减为零；第二项表示由扰动引起的稳态强迫振荡，可见当v≈1，即扰动频率ω接近自然振荡频率ωn时，系统发生共振，强迫振荡振幅最大。实际上，只要有周期性小功率扰动持续施加在源侧，均会引发不同程度的强迫振荡。

2 等效电气距离

现代电力系统特性研究大多基于经典复杂网络模型，从网络拓扑角度研究电网的结构特性及其故障扰动的传播规律[7]。但是，传统的网络拓扑模型不能准确揭示电网的本质特性[8]，而从电气角度对电网特性进行研究，能够更真实地反映电网各节点之间的电气耦合联系，更符合电网运行实际[9]。

电网中任意两节点i,j之间的等效电气距离可用这两点之间的等效阻抗Zij,eq表征，其从数值上等于从节点i注入单位电流、从节点j流出单位电流，其余节点电流为零时，节点i,j之间的电压Uij，表达式如下：

(6)

借助叠加定理，对式(6)进行改造。叠加原理示意图见图1。

图1 叠加原理示意图

综合以上可知，节点i,j之间的等效阻抗为：

(7)

因此，节点i,j之间的等效电气距离即为：

(8)

其中，Rij,eq、Xij,eq分别为Zij,eq的实部和虚部，即等效电阻和等效电抗。

3 基于等效电气距离的强迫功率振荡时空传播特性

当电力系统遭受功率振荡、负荷波动、线路投切、短路及断线故障等扰动时，系统各节点频率会产生相应波动。根据扰动传播的机电波理论，扰动信号从扰动源出发，以远低于光速的机电波形式，向电力网络各向传播[11]。在此情形下，系统各节点频率会产生较明显的过渡过程，并表现出明显的时空分布特性：不同系统节点观测到的频率偏移时间、程度及变化过程都不尽相同[12]。距离扰动源电气距离越近的电网节点，对扰动的响应时间就越短，频率信号会越早呈现出扰动特征。

根据文献[13]，频率偏移传播速度定义为观测点与扰动点的地理距离与该观测点的扰动响应延时之比，即：

(9)

式中vi为扰动点对观测点i的频率偏移传播速度，Li为观测点与扰动点之间的地理距离，Δtid为观测点对扰动的响应延迟时间。

不考虑频率扰动机电波传播的各向异性，即认为式(9)中的vi是恒定不变的，同时利用第1节中提出的等效电气距离Dij,eq表征二者之间的电气连接紧密程度，用以取代式(9)中的地理距离Li，对式(9)进行改造：

(10)

由上式可以看到：强迫振荡发生时，距离扰动源等效电气距离越近的节点，频率扰动机电波越先到达。

综上，对强迫功率振荡时空传播特性作如下总结分析：强迫振荡发生时从扰动源向系统注入扰动功率，将引起系统频率发生波动，由于电网各节点到扰动源的电气距离不同、网络参数差异等原因，导致系统各节点频率变化量呈现出明显的时空分布特性。系统各节点频率变化量响Δf应时刻存在时间差，离扰动源电气距离越近，频率变化量Δf首次达到极值的时刻就越早[14]。

图2 3机9节点系统拓扑结构

4 算例分析

为了验证强迫振荡发生时频率变化量扰动机电波传播和等效电气距离之间的对应关系，下面以美国西部WSCC 3机9节点系统为例，采用PSD-BPA软件进行仿真分析。

WSCC 3机9节点系统网络拓扑结构如图2所示，该系统中共有3台发电机，节点1为平衡节点。首先，按照第1节原理，计算得到系统各节点与3个发电机节点的等效电气距离如表1所示(结果采用标幺值)。

表1 各节点与发电机节点的等效电气距离

然后，为了验证强迫功率振荡发生时扰动机电波传播特性，分别在G1、G2、G3所在节点施加扰动幅值为原动机机械功率幅值50%、频率为0.95Hz的正弦扰动功率信号，激起系统的强迫功率振荡。在PSD-BPA软件中搭建模型进行仿真，为了更好展示仿真效果，在对每台发电机节点施加扰动功率时，给出5个系统节点的频率变化量的变化曲线以便对比。频率变化量仿真波形如图3～图5所示。

图3 在G1施加扰动功率时相关节点Δf变化曲线 图4 在G2施加扰动功率时相关节点Δf变化曲线

图5 在G3施加扰动功率时相关节点Δf变化曲线

通过表1计算结果以及上述仿真波形，分析如下：

(1)在G1节点施加扰动功率激发系统强迫振荡时，由图3可以看到，频率变化量扰动机电波到达节点1、2、4、7和9这五个节点的先后顺序依次是：节点1→节点4→节点9→节点7→节点2。而由表1得到各节点到G1的等效电气距离计算值，节点1到G1距离为0，节点4到G1距离为0.0576，节点9到G1距离为0.1332，节点7到G1距离为0.2333，节点2到G1距离为0.2823，各节点到G1等效电气距离由近到远的排序为：节点1<节点4<节点9<节点7<节点2。因此，频率变化量Δf时域仿真曲线与等效电气距离计算结果能够很好地吻合，证明在强迫振荡发生时，离强迫振荡扰动源等效电气距离越近的系统节点，频率变化量扰动机电波越先到达。

(2)在G2节点施加扰动功率激发系统强迫振荡时，由图4可以看到，频率变化量扰动机电波到达节点1、2、4、7和8这五个节点的先后顺序依次是：节点2→节点8→节点7→节点4→节点1。而由表1得到各节点到G2等效电气距离由近到远的排序为：节点2<节点8<节点7<节点4<节点1。因此，频率变化量Δf仿真曲线与等效电气距离计算结果也能够吻合。

(3)在G3节点施加扰动功率激发系统强迫振荡时，由图5可以看到，频率变化量扰动机电波到达节点1、3、6、7和9这五个节点的先后顺序依次是：节点3→节点6→节点7→节点9→节点1。而由表1得到各节点到G2等效电气距离由近到远的排序为：节点3<节点6<节点7<节点9<节点1。因此，频率变化量Δf仿真曲线与等效电气距离计算结果仍然能够吻合。

5 总结

本文基于等效电气距离理论，对电网发生强迫功率振荡时的时空传播特性进行研究，分析指出系统发生强迫振荡时，离强迫振荡扰动源等效电气距离越近的系统节点，频率变化量扰动机电波越先到达。WSCC 3机9节点系统的仿真计算结果有效证明了上述结论的正确性。

下一步可以利用上述强迫振荡时空传播特性，继续开展强迫振荡的扰动源定位和抑制技术研究。