一类基于定时补充方式的备件需求量确定方法研究∗
袁 园 付兴方 吴佳康
(空军勤务学院航材四站系 徐州 221000)
1 引言
航空备件是保证战机完好的重要装备资源,良好的备件保障能力可为这种资源的持续保障提供有力支撑[1]。良好的保障能力需要两个方面来进行建立:一是正确的航材种类;二是合适的航材数量。因此为保证航材保障部门能够提高自身的航材保障能力,可以对航材保障方式进行一些灵活的改变。选用定时补充方式可以在一定程度上减少基层保障单位的库存压力,减少经费开支[2~5]。那么在定时补充方式下,补充时间和补充数量就是重点。通过利用实测统计和备件保障概率来进行补充时间的确定以及备件需求量的确定。其最终目的在于减少保障经费,但其军事性——备件保障概率不变。
2 定时补充方式备件保障
目前,航材保障部门的订货补充方式主要是年度计划,用来确定后年的备件需求数量。时间跨度较大,不确定因素会随着时间的延长不断增加,对于保障效能带来了极大的挑战。若是采用定时补充的方式:一是可以减少部队库房的库存压力,让库房有限的空间存放更加重要的备件;二是减少因备件的储存而产生的存储费用,减少保障经费。所以,若是在一定程度上采用定时补充的方式会对航材保障工作带来积极的影响。
定时补充是指当基层备件库房备件不断减少时不要求立即补充,而是过一段日历时间,对库房的备件进行一次性补充到位,到达要求的数量。
定时补充是每个补充间隔T内,以备件的平均可用度最大为约束条件确定的。在每个补充间隔T内,平均工作时间为
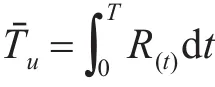
平均不能工作时间为
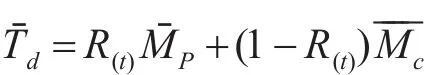
则备件可用度为
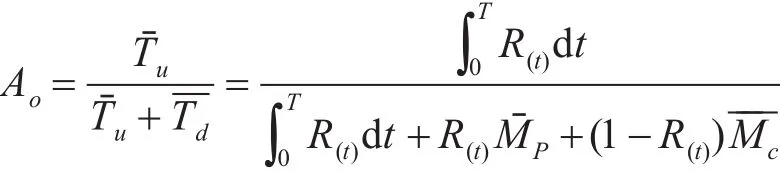
式中:R(t)为T时间内系统不发生故障的概率;为平均预防性维修时间;----Mc为平均修复时间。
若是利用求导的方法求出可用度Ao的最大值,则可以得出定时补充的最佳时间T,但是较为困难,若是利用实测统计的方法,令:
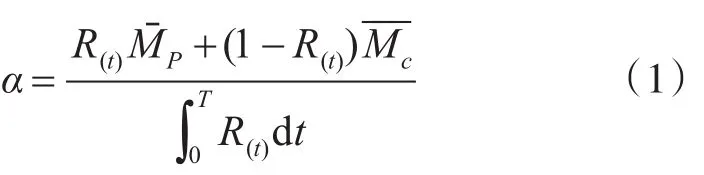
则当α最低时,Ao则最大,T则是最优的订货时间[6]。
3 备件需求确定模型
本文的备件需求计算模型主要是针对保障过程中处于磨损的、不可修的备件进行建模。与其他备件需求预测的模型相比而言,基于保障概率的备件需求计算模型更能实现装备的优化权衡和科学发展。备件保障概率是指在规定的时间内,出现备件需求时能够得到保障的概率[7~13]。
3.1 保障概率模型的建立
对于备件保障,要计算其备件保障概率,可以通过定义一个更新过程,利用更新过程理论建立备件保障概率模型。设Xi(i=1,2,…,n)为备件所在系统第i个备件的寿命,定义需要n个备件后,系统连续工作时间为一个序列。

则当备件在补充时间T内,发生i次故障,根据更新过程理论,即当需要备件数量为i件的备件保障概率为
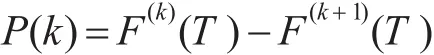
式中:F(k)(T)为F(t)的k重卷积函数,可得备件保障概率为
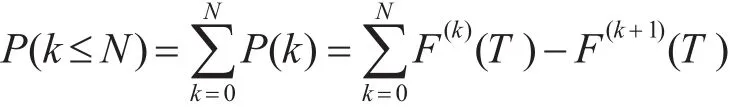
当备件寿命服从故障率为λ的指数分布,可见备件的故障密度函数和备件的累计故障分布函数分别为
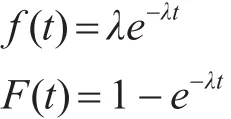
则当最佳补充时间内,F(t)的k重卷积计算公式为
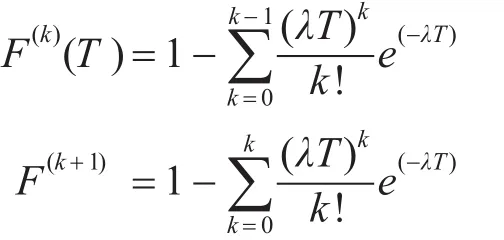
故备件保障概率为
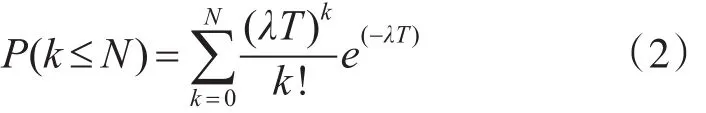
3.2 备件确定的过程
备件需求量确定的过程是在定时补充的最佳补充时间T和备件寿命服从指数分布情况下,求解使得满足规定保障概率的最少备件数量N,其主要步骤如下:
1)运用实测统计法确定最佳补充时间;
2)确定保障概率P*,从国外保障实践以及结合我国实际情况,P*取值应该在0.80~0.90之间;
3)令 k=0;
4)根据式(2)计算,若 P(k≤N)大于等于规定的保障概率 P*,则算法结束,k*=k;否则k=k+1,重新带入计算。如图1。
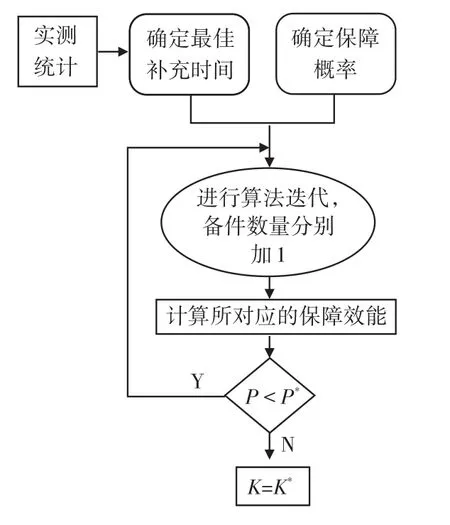
图1 计算流程图
4 算例应用
某型飞机阀门寿命服从λ=0.01的指数分布(其可靠度统计情况如表1所示)。该产品若是采用定时 补充的方式作为补充-方式,平均预防维修时间为1h,平均换件时间是0.5h。给定保障概率为0.80。

表1 某型阀门可靠度
1)根据表1绘制可靠度曲线,如图2。
2)将可靠度以50h为单位,分成若干矩形,其面积为 S1,S2,S3,S4,S5,S6,S7,S8,则
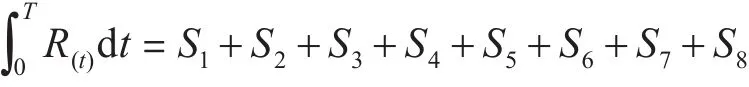
3)根据计算结果,可画出α的变化曲线,如图3。
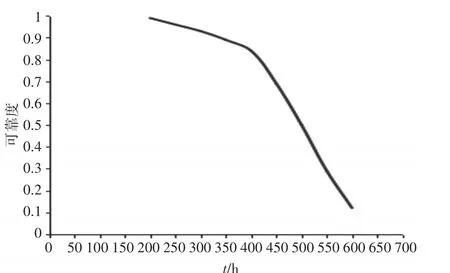
图2 可靠度曲线
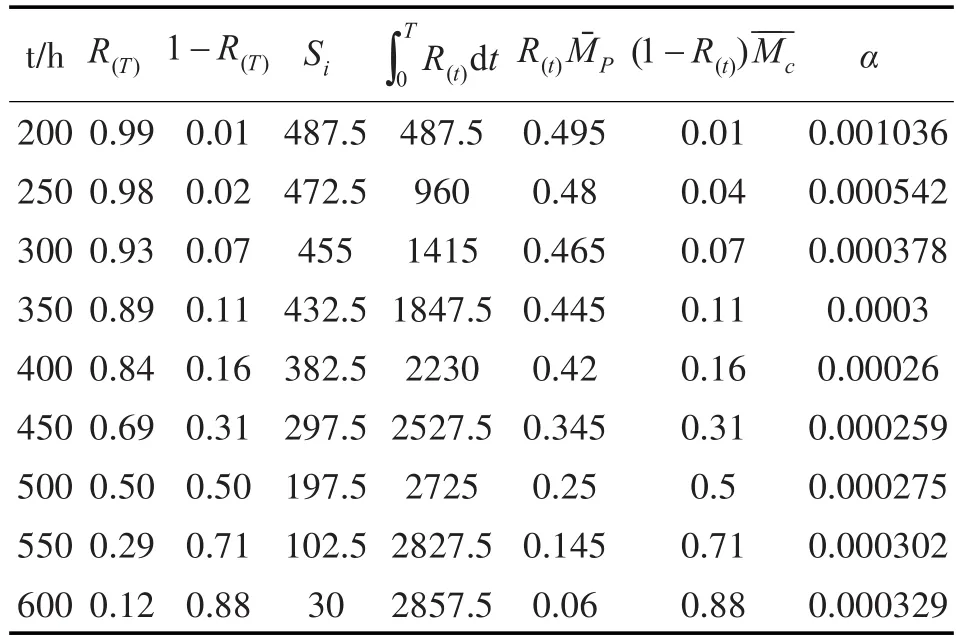
表2 阀门不可用系数α的计算值
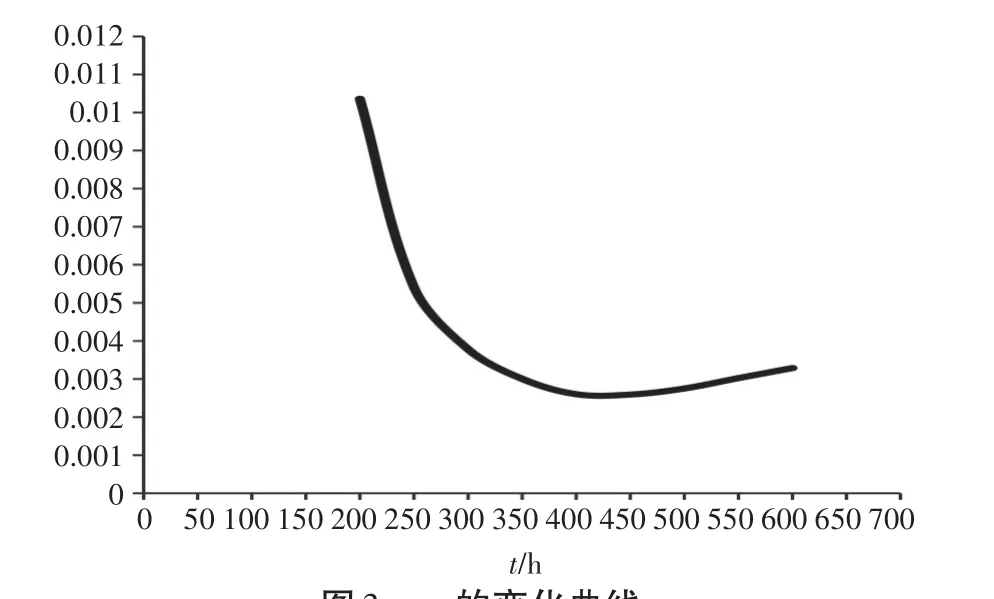
图3 α的变化曲线
由α的变化曲线可知,α的最低值为0.00024,最佳补充时间T≈430h。
在给出保障概率为0.80,将T≈430,λ=0.01带入式(1),解得所需备件数量为6个。
5 结语
与保障费用用来作为约束条件确定备件需求的不同,本文考虑的是可用度来确定定时补充下的最佳补充时间与保障概率相结合,通过备件寿命服从指数分布来确定备件保障概率模型最终确定备件的需求量。该方法应用方便,计算简单。

