基于FPGA的快速哈夫曼编码设计

陆哲敏 易庆阳 杨一凡 蒋剑飞

摘要：针对不同的应用场景，给出两种方案，一种用码表实现，另一种用静态编码实现。码表方式将题目与实际应用结合起来，针对不同场景给出不同的码表快速编码；不过考虑到无规律信号的编码，所以通过静态编码使我们的作品更加具有普适性，我们还采用三位范式编码的方式，缩短输出周期；同时在数据输入结束之前开始排序，减少编码实际占用的时间。

关键词：哈夫曼编码；静态编码；码表；范式；应用

0 引言

哈夫曼编码是基于带权路径最小的最优二叉树啥夫曼树的一种平均码长最短的编码方式。哈夫曼编码常用于数据的无损压缩，尤其在卫星探测、医学图像处理、雷达测试系统等领域有着广泛应用[1]。

以对一段长度为256的0-9的数据进行编码为例，如果采用定长编码，则需要4位表示一个0-9的数字，一共需要4*256=1024位实现编码，而如果采用哈夫曼编码可以大大降低需要的位数。

1算法设计

在开始设计前，我们先对目前主流啥夫曼方案作简单分析：

1.静态编码：编码速度与资源占用方面都在合理范围内，虽然编码速度比码表慢，但是通用性要比码表好：

2.动态编码：动态编码依据的是一棵动态变化的哈夫曼树，每个数据的编码都是由它前面所有数据组成的哈夫曼树决定的，虽然可以同步输出编码序列，但是对资源占用较大；

3.码表方案：码表只针对特定分布的数据可以获得良好压缩率，但是有着其极小的资源占用和无需复杂运算的优点。

经过以上分析，我们选择码表和静态编码相结合的方式进行编码。在输入完成前，对输入序列的分布进行判断，如果符合码表的分布要求，则直接由码表编码，加快编码的速度，如果不符合，则进行静态编码，以实现编码速度和压缩率的平衡。

为实现哈夫曼编码，我们将整个系统分为5个模块：统计、排序、编码、码表和输出。

数据由数据源输入之后，首先对其统计与排序。在整个过程中，排序进行两次，第一次在第251个周期，用于判断使用码表还是静态编码：第二次则根据编码方式的不同而改变：如果使用码表编码，则在第256个周期开始排序：如果使用静态编码，则在第254个周期排序，这是由于最后两个权值对压缩率影响极小，所以通过丢弃最后两个权值信息加快编码速度。

为了进一步减小资源占用与输出周期，编码和码表模块输出的码长均由3位构成，这样设计比起4位输出时要节省10个周期。理论支撑是出现码长为9的情况时，数据频率需要满足第i个数的码长大于前i-2个数的码长之和，这种情况的概率是极小的：而且即使出现码长为9的情况时，最大的4个码长——9、9、8、7也可以用8、8、8、8来近似，由于最大码长对应的数据的频率很小，压缩率的损失也很小。故码长为9的情况可以舍弃，所以认为码长在1-8之间，用3位二进制来表示。

1.1 统计模块

统计模块的功能是对输入的数据统计出现的频数。设计的思想是给0到9每个数字构造一个计数器，先初始化计数器值为0，每次輸入一个数字之后其相应的计数器加1，这样，在数据全部输入完成后即可得到0到9这10个数字的权重。

1.2 排序模块

排序模块的功能是对已经统计好的数据进行排序。设计的思想是：将每个权值都两两比较一次，由比较结果就可以快速确定它在一个降序排列的存储器seq中的位置。由于这些比较都是并行的组合逻辑，所以只需要读一次比较结果，一个周期即可完成排序。

1.3 码表模块

排序模块的排序结果作为码表模块选择何种编码方式的判断依据，当序列接近于等概率分布时，哈夫曼编码基本等效于等长编码，此时进行静态编码效率较低，所以通过码表1直接编码；除此之外，当序列分布范围极广，即分布十分不均匀的时候，用静态编码效率也比较低，此时采用码表2进行编码。两张码表如表1、表2所示。

1.4编码模块

如果码表模块无法对输入数据进行编码，则必须通过编码模块完成静态编码。

编码过程是由构建哈夫曼树和分配码长两个过程组成的[4]，此模块中我们使用到3个存储器，一个是上文提到的seq，记录排序好的十个数据以及各自权值；另一个存储器是node，是由哈夫曼树中的非叶节点构成的；而最后一个存储器为result，保存整棵哈夫曼树。

10个叶结点组成的哈夫曼树应有19个结点，但是根结点不参与编码，所以result只保存18个结点，同样，node结点也只保存8个内部结点。

为了提高编码效率，构建node存储器和构建result存储器是同步进行的，而构建哈夫曼树和分配码长的操作均为两个结点同时操作，编码过程也没有选择常规的自底向上的编码，而是选择了自顶向下的编码方式，避免重复读取内部结点[5]，如此下来，构造result的过程耗时10个周期，编码过程最快只需耗时8个周期。

具体过程如下：

假设已有：降序排列的权值序列seq= {seq0，seq1，seq2， seq3， seq4， seq5， seq6， seq7， seq8. seq9），初始化好的存储器为node={FFH，FFH……，FFH）。

1）第1个周期开始构造内部结点node存储器：

a）依次从seqn、seqn-l、nodek和nodek+l中寻找最小的两个值（如果权值相同，认为排前面的权值小）；

b）将最小的两个权值相加后放入node中；

c）将n、k作相应移动；

d重复a。

2）第2个周期开始同步进行哈夫曼树result存储器的构造：

a）依次从seqn、seqn-l、nodek和nodek+l中寻找最小的两个值（如果权值相同，认为排前面的权重小）：

b）将两个最小权值依次放入result中；

c）将n、k作相应移动：

d）重复a。

3）第11个周期开始编码：

a）初始码长result[17]=result[16]=1；

b）根据标记位，可以知道某一个结点是否有子结点；

i.如果有子结点，给子结点分配码长：如果子节点已经是树尾，则编码结束：

ii如果没有子结点，排查下一个结点。

4）输出码长数据，即按O～9顺序输出编码结果。

1.5 输出模块

输出模块主要有三个工作：存储输入数据、求范式哈夫曼编码、对输入数据编码并输出。具体介绍求范式哈夫曼编码[6]工作：

编码模块工作完成后，输出模块开始接收码长信息（code_length），同时记录每个码长出现的次数（size_of_len）相順序（code_order），然后根据这些信息求出每个符号的范式哈夫曼编码。

如表3所示，第一行表示code的位，第一列表示码长。把码长1出现的次数二进制值对齐第8位，把码长2出现的次数二进制值对齐第7位，以此类推，最后将表格按行相加，即得到数i的编码。

2 验证分析与FPGA实现

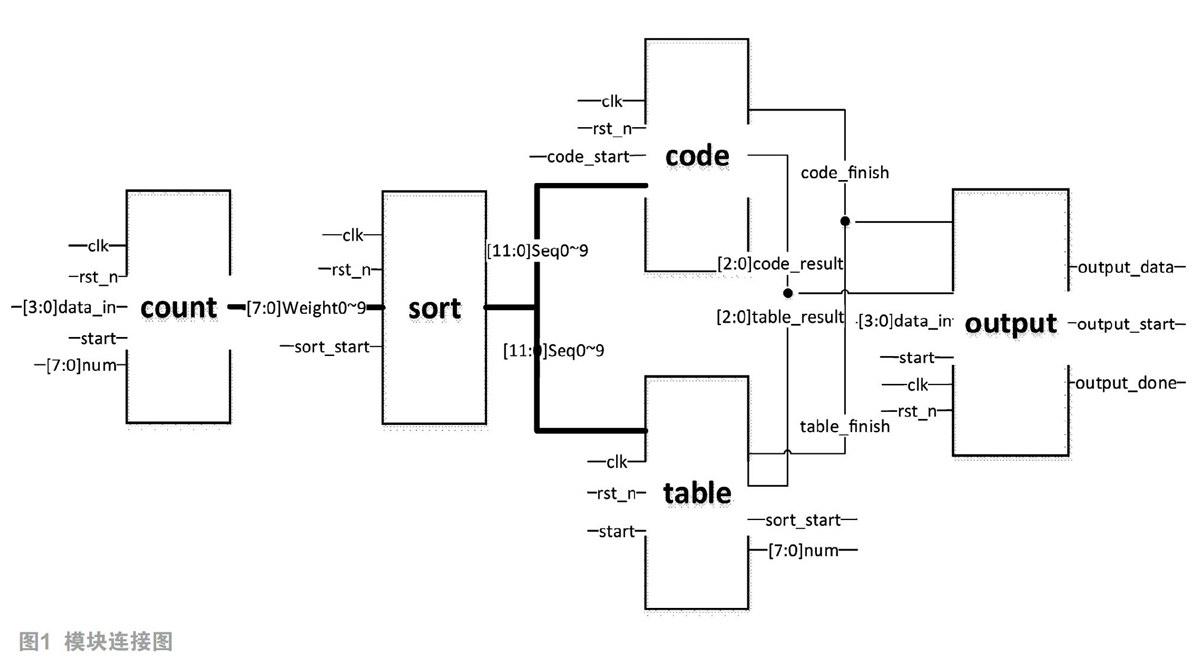
根据前述的算法设计，最终得到如图1所示的模块连接图。

为了验证编码的准确性，首先采用C++编写常规的静态哈夫曼编码算法，同时在TestbencH中，采用读写文件的方式将输出结果就保存到文件中，最后再验证两者输出的一致性。

对于题目提出的Totalcycles参数，它主要包含了输入数据的256个周期，编码用时以及输出用时。我们的输出用时包含2个部分：一是输出范式编码表，总计30个周期；二是输出编码序列。所以Totalcycles=256+编码用时+ 30+编码序列长度。根据测量结果，Totalcycles最优为码表2的547个周期，最差为码表1的1159个周期。

对于压缩算法的另一个重要指标压缩率，这里定义为编码后的数据长度与编码前的数据长度之比[7]，根据测量结果，最优压缩率为25.20%，最差为85.06%，同样分别发生在表1和表2。

在目标器件XC7A100T-1CSG324C上综合实现后，可以得到我们的设计一共使用了1819个查找表和785个寄存器：同时调用了Block Ram的lP核用于存储输入的256个序列。在将扇出约束为50的情况下，由时序报告可知8.600ns的时钟下还有0.025ns的余量，经计算此时的工作频率为ll6.28MHz[8]，关键路径位于编码模块的哈夫曼树构造过程。

在FPGA上，运用Vivado Logic Analyzer验证后，得到的波形与预期结果完全一致。

3 结论

哈夫曼编码从被提出开始，就一直被关注和研究。经过60多年的发展，它已经被广泛应用于数据压缩的各个领域。

我们的设计的主要有以下特点：

1）与实际应用场景结合起来，提供了两个码表和一种静态编码的方案。在输入数据符合码表条件时，自动调用码表加快编码速度。

2）采用范式编码的方式输出，易于解码，并使输出哈夫曼编码表的过程缩短4～24个周期。

3）采用3位码长输出，在几乎不损失压缩率的情况下，将输出码表的体积减小25%。

4）采用预先编码方案，进一步缩短编码耗时。

最初的方案中，静态编码耗时共需要70多个周期，后来几经优化，利用FPGA同步处理的优势，最终降到19个周期，加上预先编码方案，实际占用为17个周期。

在判断使用表1、表2或使用静态编码的时候，设计采用了数据频度的极差作为条件，但是在实际测试中我们发现极差并不是特别准确，真正的码表选择和数据分布有着极为复杂的关系，最终我们只能通过收紧判断条件，更多的采用静态编码以避免加速失效。所以码表和码表的选择条件，还需要更多的实验检验和数学证明。

参考文献：

[1]Latha Pillai，“Huffman Coding”EXILINX， Virtex Series， XAPP616 （vl.0） Apr 22， 2003

[2]方敏，泰晓新动态哈夫曼编码的数据压缩方法[J]计算机世界，1994（7）：29-33

[3]Matai， Janarbek，J Y Kim， and R Kastner”Energy efficient canonical huffman encoding.”IEEE， International Conference On Application-Specific Systems， Architectures and ProcessorslEEE， 2014：202-209

[4]李伟生，李域，王涛一种不用建造Huffman树的高效Huffman编码算法[J].中国图像图形学报，2005，10（3）：382-387

[5]林建英，伍勇，李建华，等一种易于硬件实现的快速自适应哈夫曼编码算法[J]大连理工大学学报.2008，48（3）：436-440

[6]张全伙，于洪斌，林榆优化哈夫曼编码数据压缩技术及程序实现[J]华侨大学学报（自然科学版）.1995，16（3）：344-348

[7]张颖超基于FPGA的Huffman编码并行实现及高速存储系统设计[D]长安大学，2015

[8]Latha Pillai，“Huffman Coding”EXILIN×， Virtex Series， XAPP616 （vl.0） Apr 22， 2003