有限元模型的整体刚度矩阵集成
罗 帅,朱佳洋,梁超锋,刘 伟
1)绍兴文理学院土木工程学院, 浙江绍兴 312000;2)广东交通职业技术学院, 广东广州 510650
在结构的有限元分析过程中,对于所划分的单元体,在求得单元刚度方程之后必须建立整个计算模型的整体刚度方程[1-5].完成这一步的关键在于怎样将单元的刚度矩阵组装成整体刚度矩阵[6-9].罗少云等[10-11]根据结点平衡方程建立整体刚度矩阵,这些方法直观易懂,但是不能提供编写有限元分析程序的合理思路;BORESI等[12]使用Boole连通矩阵进行刚度矩阵的推导,这种方法数学意义直观,但计算效率较低;LI等[13]使用对号入座法来构造结构整体刚度矩阵,但是这种方法编程效率较低,且不适合处理单元结点耦合的问题,只适合分析自由度数较少的结构体系.本研究对有限元模型分析中整体刚度矩阵的集成方法进行了分析,采用关联表法建立了有限元整体刚度矩阵的集成方法,所得结果对加强有限元建模过程的理解以及大规模有限元模型分析的开展具有指导意义.
1 利用能量原理建立整体矩阵
如图1所示的平面桁架结构,包含6个结点,每个结点有2个自由度,因此结构的整体刚度矩阵为12阶,组成桁架结构的杆单元弹性模量为E, 单元截面积为A, 单元长度为L, 设单元在整体坐标系下的倾角为θ, 则在整体坐标系下的单元刚度矩阵(为对称矩阵)可表示为[14]
(1)
杆单元轴向变形在整体坐标系下表现为结点沿水平坐标轴的位移.将结点位移矢量在整体坐标系下记为D, 则结点的位移可以表示为
D=[U1V1U2V2…UnVn]T
(2)
其中,U和V分别为桁架结点的位移在整体坐标系两个坐标轴上的投影,下标为单元结点编号,在此分析模型中n=12.

图1 桁架结构平面图Fig.1 Plane truss structure
进一步,将所分析的单元(编号为ij)结点位移矢量在整体坐标系下记为Dij, 则该单元节点的整体位移表达式为
Dij=[LUiVi…UjVj…]T
(3)
其中,U和V分别为结点i和结点j的位移在整体坐标系两个坐标轴上的投影,这里省略了其他结点的位移.因此有
Dij=Lij·D[UiViUjVj]T
(4)
式(4)中的Lij是一个构造的矩阵,功能是从桁架结构的整体位移向量中提取出与单元刚度矩阵相对应的单元位移向量,其表达式为
Lij=
(5)
其中,下标为元素所在的行和列.
将单元ij的弹性应变能(标量形式)写成内积形式为
(6)
将式(4)代入式(6)中可得
(7)
已知此单元的弹性应变能在整体坐标系下保持不变,其内积形式为
(8)
对比式(7)和式(8),可得单元刚度矩阵在整体坐标系下可表示为
Ke=LTijkLij
(9)
由式(9)求得的整体刚度矩阵是一个过渡性的矩阵,由于刚度矩阵为对称矩阵,因此可以略去上标转置符号.结构的弹性应变能在整体坐标系下写成内积形式为
(10)
根据能量原理,结构的弹性应变能就是结构内部构件的应变能之和,即
P=∑Pe
(11)
将式(7)代入式(11),可得
(12)
对比式(10)和式(12),可得单元刚度矩阵为
K=∑LTijkLij
(13)
式(13)即为基于能量原理,在已经推导的单元刚度矩阵k的基础上,通过构造功能矩阵Lij推导的有限元模型的整体刚度矩阵建立的方法.该方法揭示了从单元刚度矩阵到结构整体刚度矩阵的过程,运算可知该方法的本质就是将单元刚度矩阵的元素,按照结构构件的联接规律置入整体刚度矩阵的相应位置上.该方法具有物理意义明确、推导过程严谨、便于理解的优点,但是转换过程较为复杂,本研究引入关联表以简化整体矩阵的建立过程.
2 利用关联表建立整体矩阵
由式(9)可知,集成总体刚度矩阵的过程就是将单元刚度矩阵中的元素,按照构件结点的联接规律置入整体刚度矩阵的相应位置.
根据这一规律,对图1所示的模型,将各单元的单元编号与整体结点编号的对应关系列于表1.该结构结点号码表确定了每个单元的结点位置,这里称之为关联表,可以把它作为有限元编程过程中要求输入的基本数据之一.随后利用关联表1,通过定位运算得到各结构单元的关联向量(表2)可推导出单元刚度矩阵各元素在结构整体刚度矩阵中的对应位置,不妨以图1中的单元6为例来说明具体的推导过程.

表1 局部结点与整体结点的关联表
首先,根据式(1)求得单元6的在整体坐标系下的整体刚度矩阵,是一个4阶的对称矩阵.然后,构造12阶的零矩阵作为过渡矩阵.接着,根据式(9)将求得的单元刚度矩阵各元素填充到过渡矩阵的对应位置中.由表2可知,其关联向量(行向量)为[3 4 7 8],构造一个与关联向量同阶的全1行向量[1 1 1 1],求这两个行向量的直积[6],得到所有16个元素的行位置[5].交换两个向量的顺序,再次求得两个行向量的直积,得到所有16个元素的列位置,根据行列指标的定位,将单元刚度矩阵的元素置于过渡矩阵的相应位置中完成这一步.最后,应用式(13)对各个单元所求得的过渡矩阵求和,得到结构的整体刚度矩阵.

表2 关联向量计算表
由式(1)可得单元6的单元刚度矩阵,它是一个4阶的对称矩阵.连接单元6的结点为结点2和结点4,每个结点的自由度为2.根据直积运算求得的指标向量可知:单元刚度矩阵第1行、第1列的元素k11在整体刚度矩阵中的位置是第3行、第3列;第1行、第2列的元素k12在整体刚度矩阵中的位置是第3行、第4列;第1行、第3列的元素k13在整体刚度矩阵中的位置是第3行、第7列;第1行、第4列的元素k14在整体刚度矩阵中的位置是第3行、第8列;依此类推,可得第2、3、4行各个元素在整体矩阵中的位置,从而建立单元6的过渡矩阵kt6. 值得指出的是,当以显示的形式求出每一个单元的过渡矩阵时会消耗大量的计算资源,但是以隐式的形式求和直接得到整体刚度矩阵时可以显著提高计算效率.
由于结构的整体刚度矩阵集成是有限元编程中的重要环节,因此其推导过程对运用有限元方法获得正确分析结果至关重要,本研究采用的关联表方法简化了整体矩阵的建立过程,能有效节约计算资源,适合编程实现,对大型有限元模型分析的开展具有指导意义.
3 算例分析
图1所示的平面桁架,其所受到的外荷载已在图中标出,已知各杆件的材料物理属性为EA=2×108N, 试求各杆件内力.
1)建立单元刚度矩阵.根据图1中各节点的几何坐标,采用式(1)推导各单元刚度矩阵kei. 以单元6为例,由单元6的整体坐标位置可得单元长度L=4 m,单元倾角θ=36.87°, 由式(1)得到单元6的单元刚度矩阵(为简化这里略去单位,下同)为
(14)
2)建立结构各单元的过渡矩阵.建立与整体刚度矩阵同阶的全零矩阵作为过渡矩阵(本例模型有6个结点,每结点2个自由度,共12阶),根据单元节点的连接关系建立结构关联向量(表2).以结点6为例,其关联向量(行向量)为[3 4 7 8],构造一个与关联向量同阶的全1行向量[1 1 1 1],求这两个行向量的直积[15](也叫Kronnecker张量积),得到所有16个元素的行位置为
[3 3 3 3 4 4 4 4 7 7 7 7 8 8 8 8].
交换两个向量的顺序,再次求得两个行向量的直积,得到所有16个元素的列位置为
[3 4 7 8 3 4 7 8 3 4 7 8 3 4 7 8].
把单元6的刚度矩阵各元素按行排成一个行向量,根据得到的行列指标定位,将此行向量的各个元素置于过渡矩阵kt6的相应位置,得到相应单元的过渡矩阵为
(15)
3)建立结构整体刚度矩阵.将所求得的各单元过渡矩阵加起来得到结构整体刚度矩阵为
(16)
值得指出的是,因为还没有考虑边界约束,此步骤得到的整体刚度矩阵是一个奇异矩阵.
4)施加边界条件,由于结点1在水平和竖直方向的位移被约束,即在结点1上水平和竖直方向的位移为0,结点4在竖直方向的位移被约束.即在结点4上竖直方向的位移为0,采用划0置1法[16]将这些边界条件应用到建立的整体刚度矩阵KG中,得到修改后的整体刚度矩阵K为
(17)
5)施加荷载并建立结构刚度方程.由于荷载均施加在结点6的竖直向下方向上,因此由图1直接可得
f=[0 0 0 0 0 0 0 0 0 0 0 -10]T
(18)
由此建立结构刚度方程为
KD=f
(19)
6)计算单元内力.将式(17)和式(18)代入式(19)中求解结构刚度方程,得到各结点的位移,图2中的虚线即结点位移后的结构变形图.根据得到的结点位移可求得桁架杆单元的内力,见图2中数值.由于本研究主要讨论有限元建模过程中的整体矩阵集成方法,这里不再赘述.
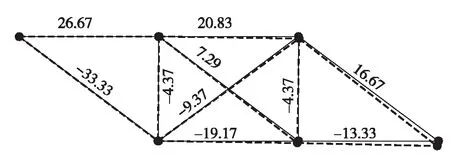
图2 单元内力(单位:N)Fig.2 Diagram of element internal force(unit:N)
结 语
本研究围绕结构有限元分析中的建模问题,推导了基于关联表的有限元模型整体刚度矩阵集成方法,结果表明,运用功能原理推导结构的整体刚度矩阵物理意义明确,便于理解;运用关联表建立的结构整体刚度矩阵有效可行;本研究基于关联表方法建立的结构整体刚度矩阵不仅适合桁架结构,对其他结构也适用.

