基于井网单元的非均质低渗透油藏产能计算方法

刘今子， 邸伟娇， 宋考平， 高 立， 董 驰， 朱维耀， 董丽娜

( 1. 东北石油大学 数学与统计学院，黑龙江 大庆 163318； 2. 东北石油大学 石油工程学院，黑龙江 大庆 163318；3. 大庆钻探工程公司 钻技一公司，黑龙江 大庆 163461； 4. 北京科技大学 土木与资源工程学院，北京 100083； 5. 大庆油田有限责任公司 供水公司，黑龙江 大庆 163453 )

0 引言

低渗透油藏的渗流特征与中、高渗透油藏的具有显著差异性，非线性渗流特征不符合达西定律。人们对低渗透油藏进行研究[1-9]。窦宏恩等[3]、王晓冬等[4]分析启动压力梯度，论证其存在性，验证非达西渗流曲线并非来自模拟结果。郝斐等[5]、李松泉等[6]通过岩心实验得到实测数据，统计回归启动压力梯度的经验公式。韩洪宝等[7]、李忠兴等[8]、朱维耀等[9]以启动压力梯度为基本渗流特征，开展渗流特征实验并进行数值模拟。这些研究将启动压力梯度函数常值化，作为固定常数代入油藏工程的计算公式，没有考虑渗透率非均质构型的影响，也没有研究对产能计算公式的影响。

目前，对油藏非均质性特征的研究主要依靠岩心实验或数值模拟方法[10-21]。笔者考虑渗透率非均质构型和启动压力梯度，建立低渗透油藏产能计算公式，通过数值模拟进行实例分析。基于井网条件下流动分区的渗流特征，引入3种典型渗透率非均质构型，结合启动压力梯度函数表征方程，建立产能计算公式，形成完整的低渗透非均质油藏的产能计算方法。

1 单相渗流产能

1.1 假设条件及典型非均质模型

假设条件：

(1)注采井间的渗透率构型简化为3种典型非均质模式；

(2)流动特征符合有启动压力梯度的非达西渗流规律。

针对实际储层渗透率构型分布的非均质特征，假定为3种典型的表征模式[14-15]。数学模型形式：

(Ⅰ)K是线性递增，K(r)=a+br，a>0，b>0；

(Ⅱ)K是对数函数，K(r)=a+blnr，a>0，b>0；

(Ⅲ)K是指数函数，K(r)=aebr，a>0，b>0。

其中，K为渗透率；r为地层任意点到井筒的距离；a、b为常数。

1.2 启动压力梯度

采用实验数据进行回归，得到低渗透油藏的启动压力梯度与渗透率的函数关系为

G=λKnd,

(1)

式中：G为启动压力梯度；λ、nd为回归参数。

1.3 产能

当渗透率K为常数时，将K(r)=K代入启动压力梯度G，得到低渗透油藏的产能计算公式为

(2)

即

(3)

式中：Q为产量；p为压力；μ为黏度；h为厚度。

将压力p和井距r的积分上下限代入式(3)得

(4)

式中：pe为注入压力；pw为井底流压；re为井筒半径；rw为泄压半径。

1.3.1 线性递增型

将K(r)=a+br代入式(1)和式(4)，得到基于渗透率构型(Ⅰ)的产能计算公式为

(5)

1.3.2 对数函数型

将K(r)=a+blnr代入式(1)和式(4)，得到基于渗透率构型(Ⅱ)的产能计算公式为

(6)

式中：Г为伽玛函数。

1.3.3 指数函数型

将K(r)=aebr代入式(1)和式(4)，得到基于渗透率构型(Ⅲ)的产能计算公式为

(7)

式中：Ei为指数积分函数。

基于不同的渗透率构型和启动压力梯度函数，构建的非均质低渗透油藏单相渗流产能计算公式具有一般意义。当b=0时，a=K，即退化为低渗透均质油藏的产能计算公式；当b=0且λ=0时，即退化为低渗透均质油藏达西渗流的产能计算公式。

2 两相渗流产能

2.1 相渗曲线

利用岩心实验数据计算相渗曲线公式时，常用3种典型拟合函数形式：(1)幂函数(Stone相渗计算公式)；(2)指数函数；(3)多项式函数。

在实际应用中，幂函数形式和指数函数形式易超出相渗取值范围，线性拟合时产生误差扩散，所以采用第三种相渗曲线形式，即多项式函数形式：

(8)

(9)

式中：Krw为水相的相对渗透率；Kro为油相的相对渗透率；Sw为含水饱和度；an、an-1、…、a1、a0和bn、bn-1、…、b1、b0为回归参数。

2.2 启动压力梯度

低渗透油藏存在启动压力梯度，渗流特征不符合达西定律。对实验数据进行回归分析，得到油相和水相的启动压力梯度与岩心渗透率关系式为

Go=λoKndo,

(10)

Gw=λwKndw,

(11)

式中:Go、Gw分别为油相和水相启动压力梯度；λo、λw、ndo、ndw为回归参数。

水相的启动压力梯度比油相的小很多，水相的运动方程中一般忽略启动压力梯度[7]。

2.3 产能

根据低渗透油藏两相区各点的压力分布，以及相渗和启动压力梯度的关系，两相渗流的产能计算公式为

(12)

化简得

(13)

式中：μw为水相的黏度；μo为油相的黏度。

联立式(8-11)，将渗透率构型代入式(13)，整理化简得到不同渗透率构型的两相渗流产能计算公式。

2.3.1 线性递增型

将渗透率构型(Ⅰ)代入式(13)得

(14)

2.3.2 对数函数型

将渗透率构型(Ⅱ)代入式(13)得

。

(15)

2.3.3 指数函数型

将渗透率构型(Ⅲ)代入式(13)得

(16)

3 不同井网条件下产能

3.1 反五点井网

反五点井网模式见图1。注采平衡时，注入量等于4个分区的流量之和，即4个油井的总产液量。各注采单元分区的渗透率构型不同。

产量计算公式为

(17)

(18)

式中：Qi为第i个分区油井的产液量；Ki为第i个分区的绝对渗透率；Krwi为第i个分区的水相的相对渗透率；Kroi为第i个分区的油相的相对渗透率。

引入渗透率构型，计算注采单元的流动分区的产量时，根据渗透率构型的不同，选择相应的产能计算公式。

3.2 反七点井网

反七点井网模式见图2。注采平衡时，注入量等于6个分区的流量之和，即6个油井的总产液量。各注采单元分区的渗透率构型不同。

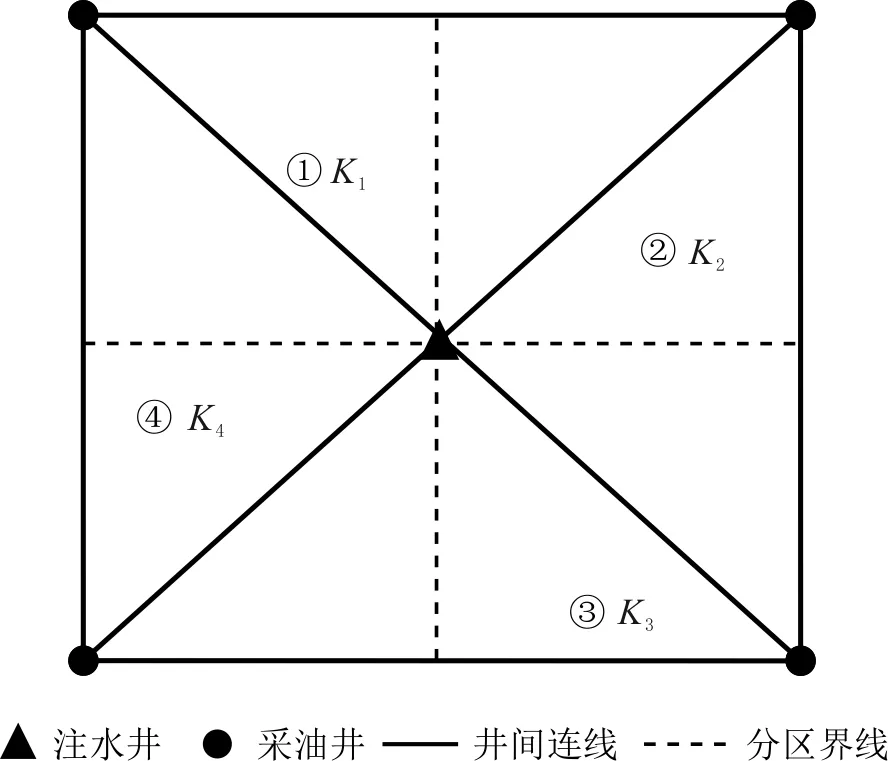
图1 反五点井网模式Fig.1 Reverse five-point pattern

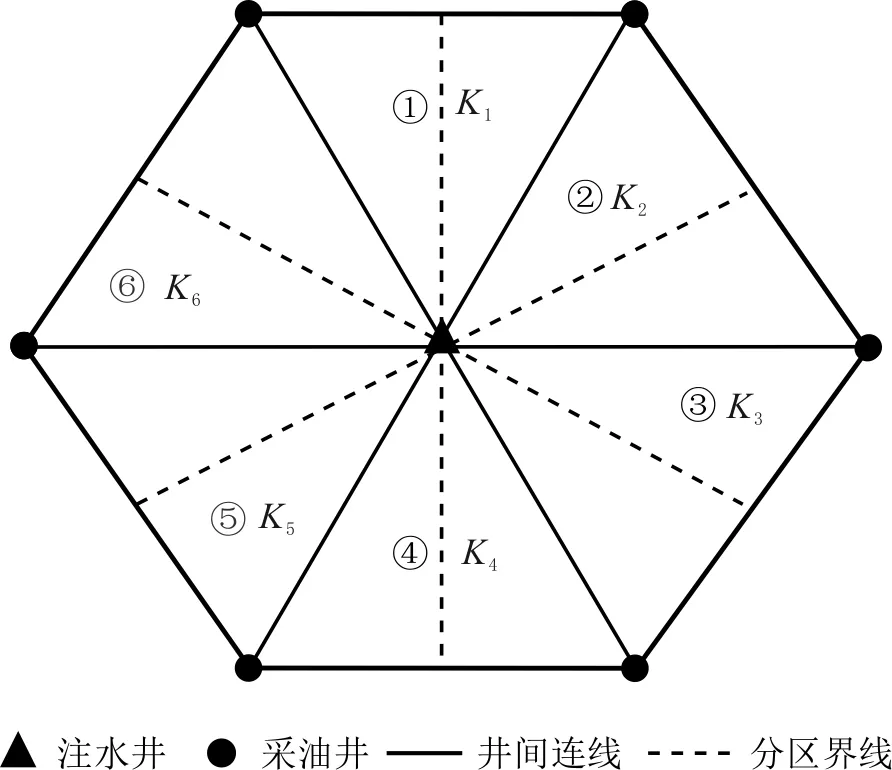
图2 反七点井网模式Fig.2 Reverse seven-point pattern

产量计算公式为

(19)

(20)

3.3 矩形井网

矩形井网模式见图3。注采平衡时，注入量等于6个分区的流量之和，即2个边井分区的流量与4个角井分区的流量之和。各注采单元分区的渗透率构型不同。

产量计算公式为

(21)

边井分区产量QBi计算公式为

(22)

角井分区产量QJj计算公式为

(23)

式(22-23)中：la为井距；lb为排距；KBi(r)为边井分区i的渗透率构型；KJj为角井分区j的渗透率构型。

3.4 反九点井网

反九点井网模式见图4。注采平衡时，注入量等于8个分区的流量之和，即4个边井分区的流量与4个角井分区的流量之和。各注采单元分区的渗透率构型不同。

产量计算公式为

(24)

边井分区产量QBi计算公式为

(25)

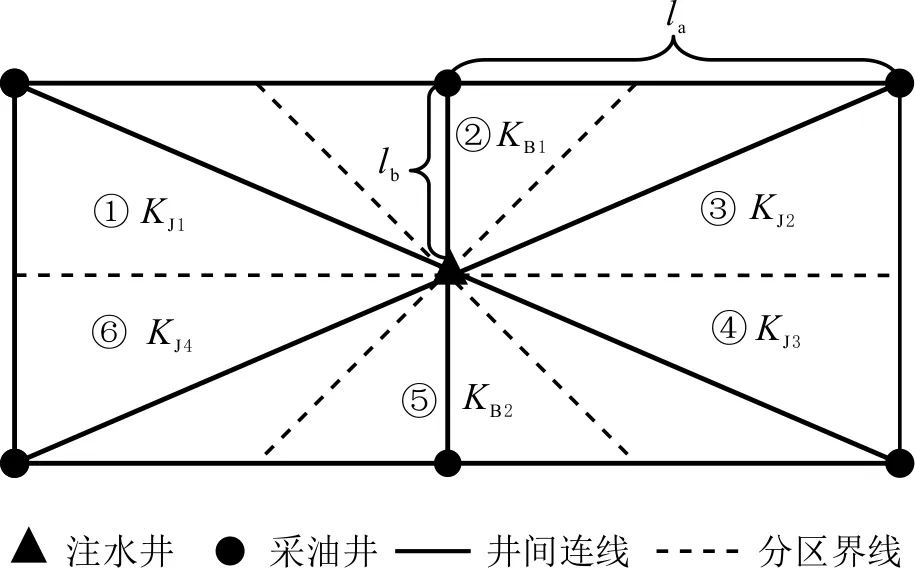
图3 矩形井网模式Fig.3 Rectangular pattern

图4 反九点井网模式Fig.4 Reverse nine-point pattern

角井分区产量QJj计算公式为

(26)

3.5 菱形反九点井网

菱形反九点井网模式见图5。注采平衡时，注入量等于8个分区的流量之和，即4个边井分区的流量、2个上(下)角井分区的流量及2个左(右)角井分区的流量之和。各注采单元分区的渗透率构型不同。

产量计算公式为

(27)

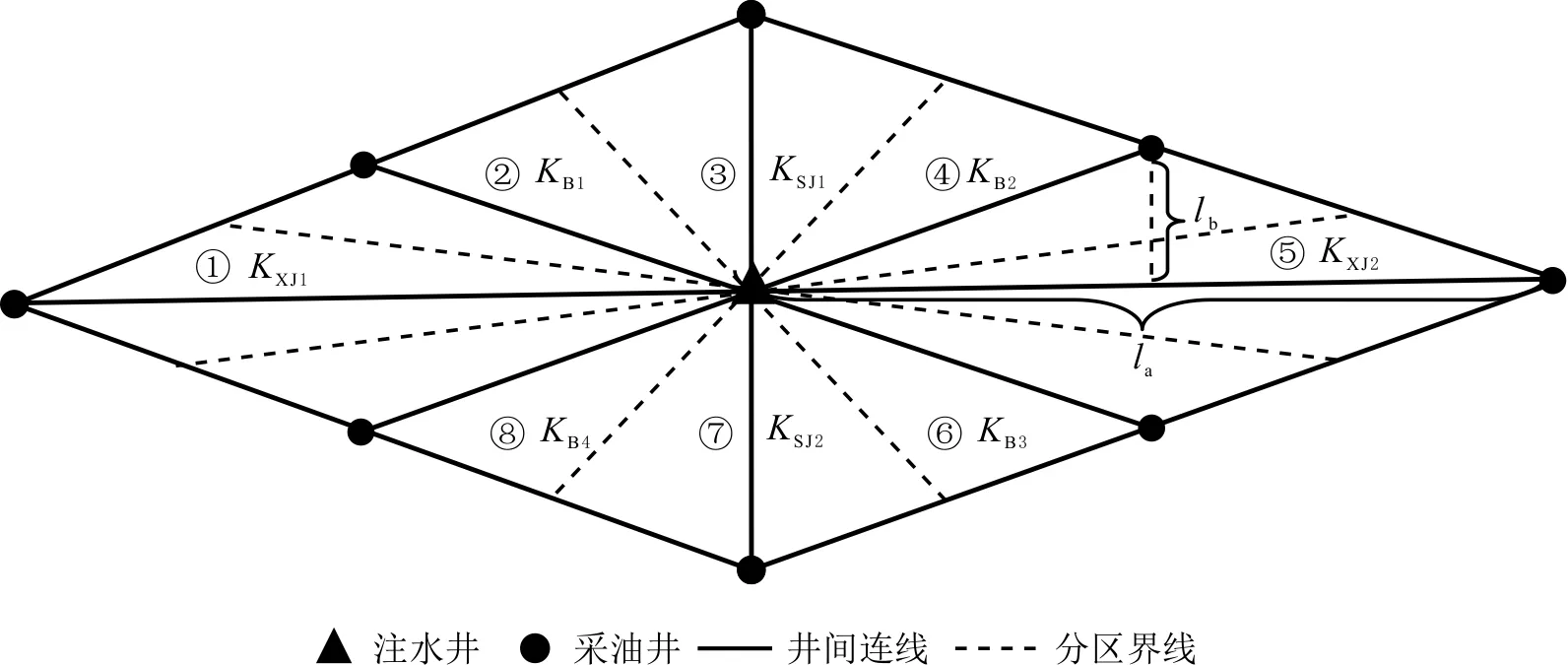
图5 菱形反九点井网模式Fig.5 Reverse nine-point diamond pattern

边井分区产量QBi计算公式为

(28)

上(下)角井分区产量QSJj计算公式为

(29)

左(右)角井分区产量QXJj计算公式为

(30)

式(29-30)中：KSJj(r)为上(下)角井分区j的渗透率构型；KXJj(r)为左(右)角井分区j的渗透率构型。

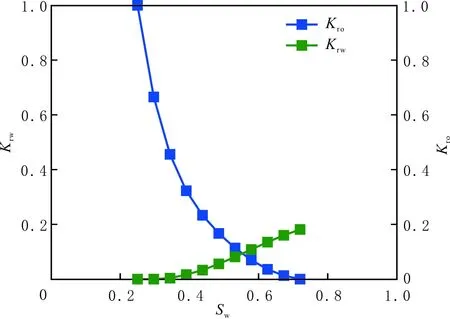
图6 某低渗透油藏相对渗透率曲线Fig.6 Relative permeability curves in low permeability reservoir

4 实例分析

某低渗透油藏的基本参数：孔隙度φ=0.12；Ka=8×10-3μm2(注水井点)，Kb=1×10-3μm2(采油井点)；油的黏度μo=5.80 mPa·s；水的黏度μw=0.45 mPa·s；井筒半径rw=0.1 m；注入压力pe=17×106Pa；井底流压pw=7×106Pa；厚度h=2 m；注入量Q=20 m3/d；注入时间t=400 d；初始含水饱和度Swc=0.25，束缚水饱和度Swi=0.78。

4.1 相渗曲线关系

利用相对渗透率曲线(见图6)，确定函数关系式为

,

4.2 分区产量

不同井网类型的井距和排距参数：(1)反五点井网，井距为200 m；(2)反七点井网，井距为200 m；(3)矩形井网，井距为200 m，排距为150 m；(4)反九点井网，井距为300 m；(5)菱形反九点井网，井距为300 m，排距为100 m。

利用建立的数学模型对不同井网类型的注采单元分区进行产能计算，数值结果见表1-5。

表1 反五点井网不同渗透率构型的分区产量

表2 反七点井网不同渗透率构型的分区产量

表3 矩形井网不同渗透率构型的分区产量

表4 反九点井网不同渗透率构型的分区产量

表5 菱形反九点井网不同渗透率构型的分区产量

5 结论

(1)将注采井间的渗透率构型简化为3种典型非均质模式代入启动压力梯度函数，构建低渗透非均质油藏产能计算公式，可以退化成低渗透均质油藏的产能计算公式和均质油藏达西渗流的产能计算公式。

(2)构建不同井网类型条件下的低渗透非均质油藏注采单元产能计算公式，利用油藏实际数据进行数值演算，可以用来计算井网的注采单元分区产能，也可以分析注采井间的渗透率非均质构型的特点。

(3)结合实际生产动态资料，利用构建的产能计算公式，可以预测注采单元的渗透率区域分布的不同非均质模式，为油藏精细描述和挖潜策略确定提供指导。