街道峡谷形态对污染物扩散的数值模拟
雷林清,崔鹏义,黄远东
(上海理工大学 环境与建筑学院,上海 200093)
机动车排放的尾气污染物及其形成的二次污染,是城市大气污染的重要来源,对其采取主动控制措施的前提是要掌握机动车尾气等污染物在街道峡谷内流动扩散及其分布的规律[1]。街道峡谷的概念最早由Nicholson[2]提出来,它是指两侧具有连续高大建筑物的狭长街道。后来街道峡谷这一概念被中国学者王宝明等[3]进行了扩展,即使街道两旁的建筑物高低不平,不连续甚至有一定的缺口也可称作街道峡谷。目前,对于街道峡谷内污染物扩散传递规律的影响研究,国内外有关科学工作者已经取得了一定的研究进展。
Yang等[4]通过数值模拟研究了街道峡谷内不同建筑物布局的空气对流对街谷内气流运动和污染物扩散的影响。Heist等[5]研究了6车道的道路结构以及隔声屏障对街谷中气流场和污染物扩散的影响,并与风洞实验进行了验证,得出在评估道路附近的空气质量时,道路布局和结构必须考虑进来。Maider等[6]基于大涡模拟(large eddy simulation,LES),研究了建筑物的屋顶结构对街道峡谷内空气流动的影响。Sanchez等[7]研究了城市街道峡谷的设计对城市交通噪声暴露的影响,但对街谷内气流运动和污染物的扩散却未作进一步的研究。作者之前利用数值仿真技术研究了带廊道,以及不同廊道尺寸的建筑物结构对街谷内气流运动和污染物扩散的影响[8],但并未系统、深入地进行定量分析,并对下沉式机动车道内污染物扩散对机动车驾驶员的影响进行进一步的分析。鉴于此,本文将基于Sanchez等[7]的研究,结合现实中街道的形状特点,构建9种2类街道截面形态(道路抬升类型和两侧建筑底部廊道)的数值模型,探究其截面形态内部流动结构与污染物浓度分布的影响。
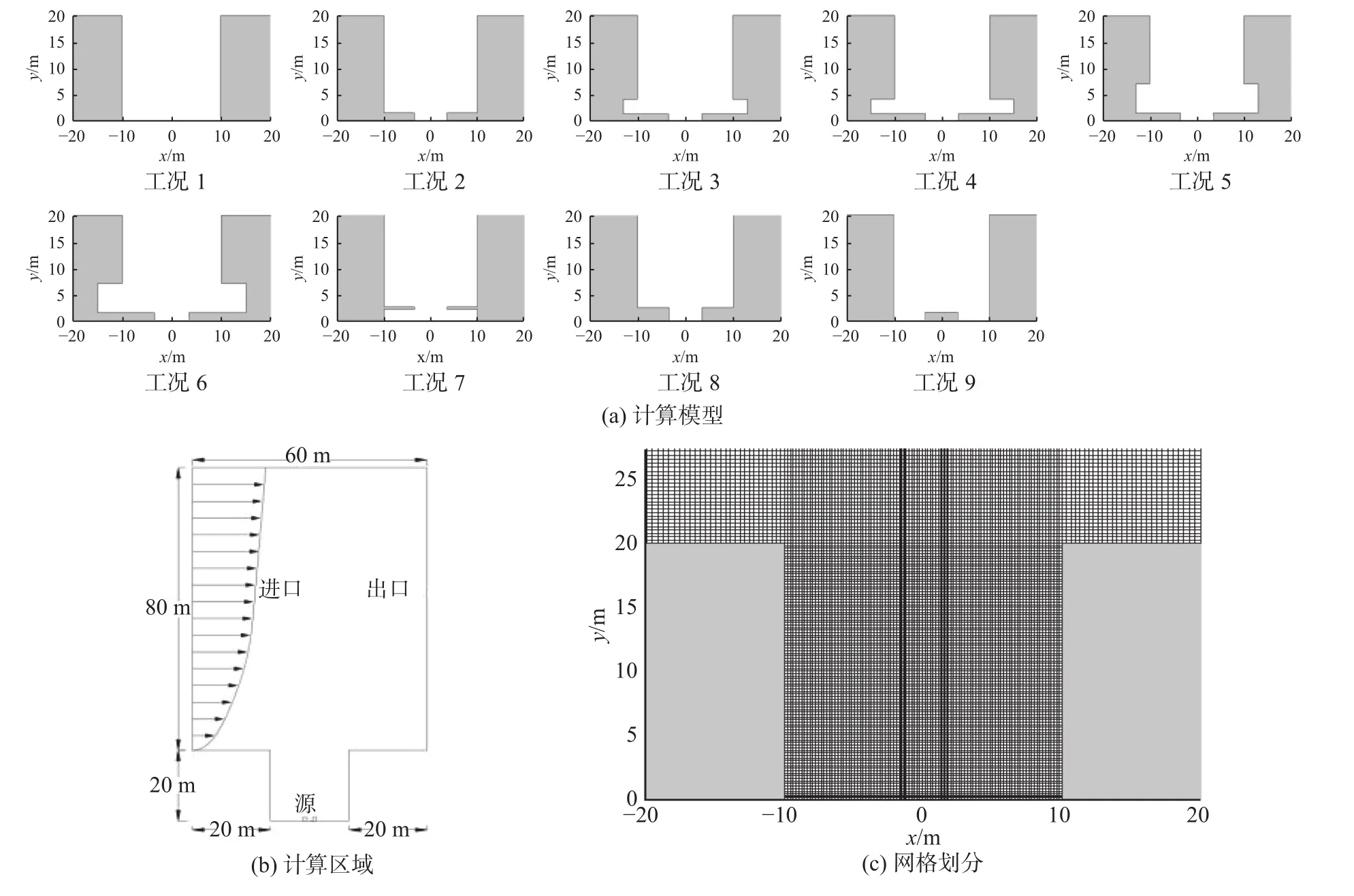
图1 计算模型、区域及网格划分Fig.1 Computational models, domain and mesh generation
1 物理模型及计算区域
由于风向垂直于街道峡谷,而且只分析街谷中流场和污染物的扩散,因此峡谷的结构可以简化为二维。图1为计算模型、区域及网格划分。
图1(a)为不同类型城市街道峡谷的二维物理模型,考虑街道两侧建筑底部廊道的深度和高度变化(工况2,3,4,5,6),以及街道内机动车道路结构变化(工况1,2,7,8,9)对流场和污染物扩散的影响,将实验工况分为9种:工况1为参考工况;工况2为深度1.7 m的下沉式道路;工况3的廊道深度和高度均为3 m;工况4的廊道深度为 5 m,高度为 3 m;工况 5 的廊道深度为 3 m,高度为6 m;工况6的廊道深度为5 m,高度为6 m;工况7的道路为两层式结构,下沉深度为3 m;工况8为深度3 m的下沉式道路;工况9为抬高1.7 m的上升道路。
计算区域及尺寸如图1(b)所示,图中街道峡谷宽及两侧建筑物高均为20 m,即街道峡谷的高宽比H/W为1,可视为理想的城市街道峡谷。两条污染源均是边长为0.5 m的正方形,位于距地面中心1.5 m处的两侧,用来模拟机动车尾气排放。本文采用结构化网格,对工况1进行网格独立性考核,比较了6种网格密度,网格数量分别为3 368,4 468,10 710,22 940,40 130 和 63 135。街道峡谷内流速及污染物浓度分布随网格密度变化,综合计算精度及时间,确定采用0.2 m的网格尺寸。如图1(c)以工况1为例,计算区域采用增长型网格,增长比率为1.01,网格总数为40 130。
2 数学模型
2.1 控制方程
通过求解描述空气流动与污染物扩散的Navier-Stokes方程、污染物组分输运方程及封闭方程的标准k-ε湍流模型,获取所构建模型的数值解。为了能够更好地利用CFD数值模拟技术来进行计算和分析,本研究的数值模拟采用以下的假设:a. 流体的热物性为常数;b. 浮升力的影响可以忽略不计;c. 街谷内的气流流动为不可压缩流动[9]。对于二维的定常不可压缩流动,其雷诺时均化的湍流控制方程[10]为
不可压连续性方程:
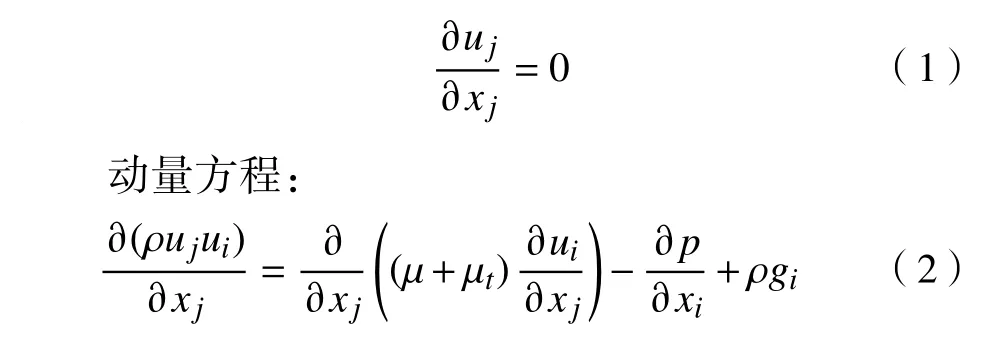
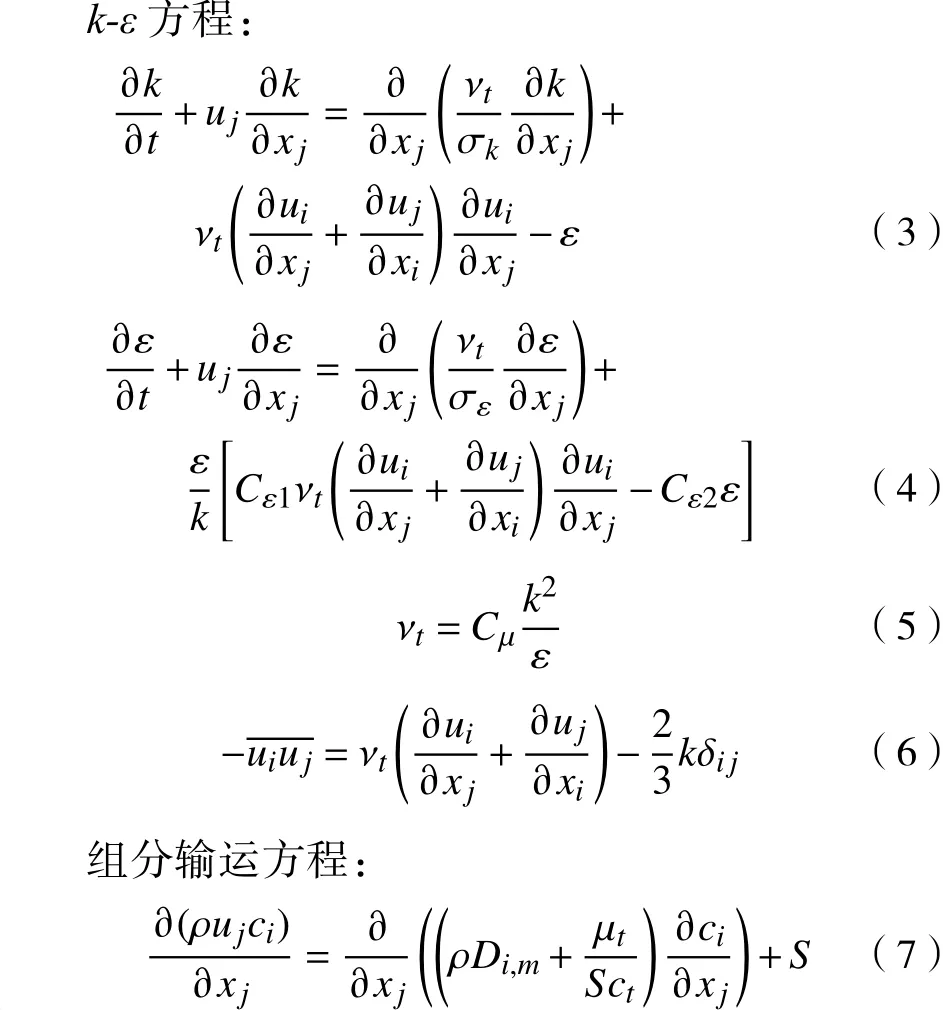
2.2 边界条件设置
a. 进口边界条件。
计算区域进口采用速度进口边界条件,进口风速按指数分布方程给定[11],即
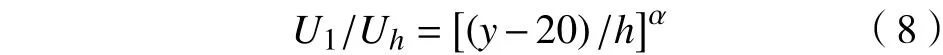
b. 出口边界条件。
出口为流动充分发展边界,即
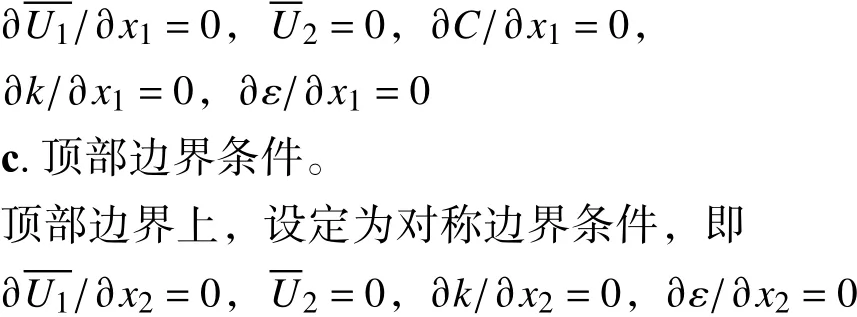
d. 壁面边界条件。
在建筑物壁面和地面上速度采用无滑移边界条件,污染物浓度采用无渗透边界条件。
1.道德认知变得比较模糊。学生在一元文化时代构建起来的价值观与核心文化,变得越来越少,学校和教师的道德权威也越来越削弱,不知道怎样的价值观和文化与值得学习和崇拜,道德认知变得比较模糊。
e. 污染源的设置。
以CO作为污染气体,因源强随交通流状态的变化而改变,为了更有实际意义,本文采用本课题组之前的研究成果来评估CO的排放[13]。源强可由机动车的综合排放因子和车流量计算得到。
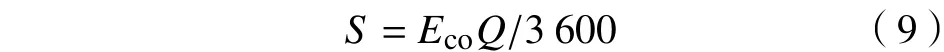
式中:Q为车流量,辆/h;Eco为机动车车组的CO综合排放因子,g/(km·辆)。CO的综合排放因子Eco与平均车速有关,其关系式为
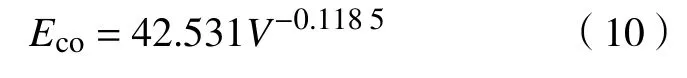
式中,V为平均车速,km/h,考虑到实际的路况和车速的限制,假设 V = 40 km/h[11]。
f. 无量纲浓度。
以无因次浓度的形式来表示所测的污染物浓度,即无量纲浓度K。其表达式为

式中:L为线源长度,m。
2.3 数值方法
本研究中采用有限体积法(FVM)对控制方程进行离散,所有变量离散格式采用二阶迎风格式。整个研究计算是在ANSYS FLUENT 14.5平台上独立完成,压力与速度耦合采用SIMPLE算法,压力项采用标准离散化方法进行处理和计算。
2.4 模型验证
本文数值模拟的湍流模型采用已验证过的标准k-ε湍流模型,具体的验证过程可参考文献[14]。文中研究不同屋顶结构对街道峡谷内流动扩散的影响,将风洞实验结果与3种湍流模型计算结果进行比较,发现标准k-ε湍流模型与风洞实验数据一致性最好。本文模型研究与其相似,故采用标准k-ε模型对其进行研究。图2为3种湍流模型和风洞实验的拟合曲线图,从图中可以看出标准k-ε模型与风洞实验结果吻合得较好。
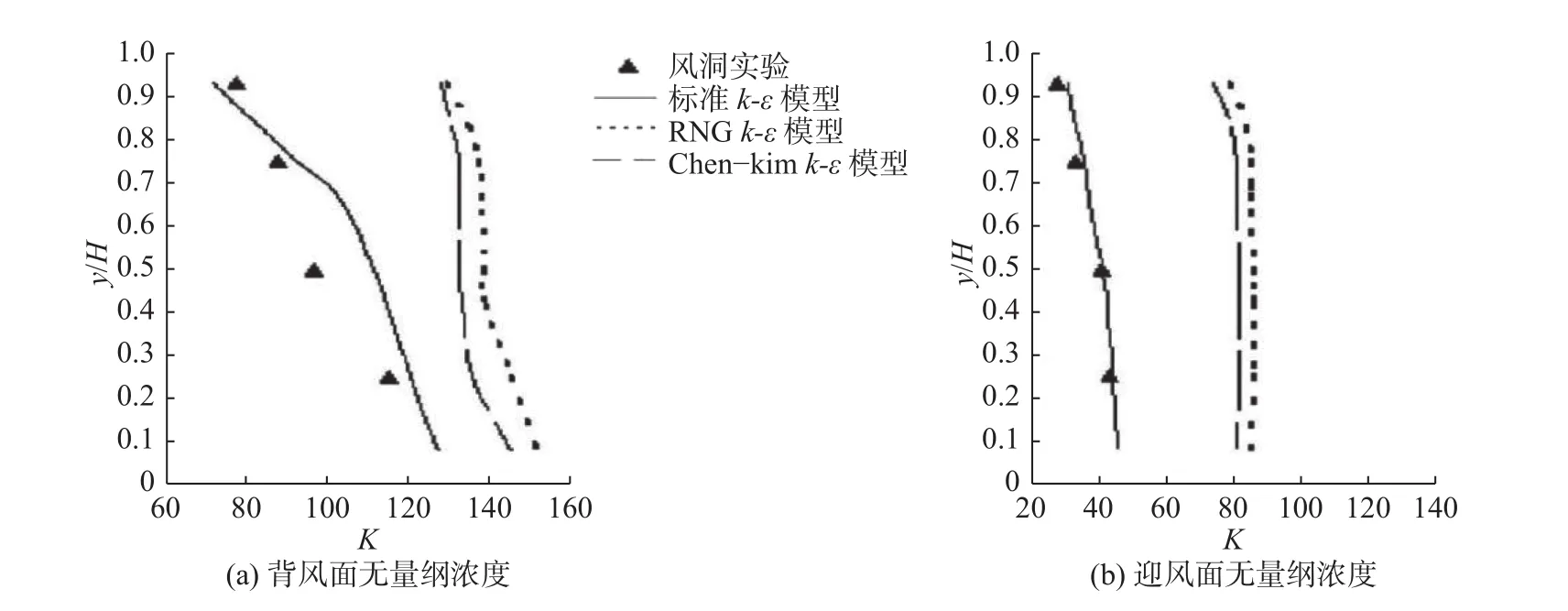
图2 模型验证Fig.2 Model validation
3 结果及分析
图3(见下页)为9种二维城市街道截面形态、街道峡谷内速度流线图和无量纲浓度云图。首先分析机动车道路结构的变化对街道峡谷内流场和污染物扩散的影响。比较工况1,2,7,8,9可知,机动车道的下降基本不会改变街道峡谷内的流动结构和污染物的分布情况,主要表现在,工况1,2,7,8中街道峡谷内都会形成一个规则的顺时针旋涡,造成污染物在背风面近地面处聚集,由近地面向高度处降低,且在街道峡谷内污染物浓度分布情况相似。另外,由于机动车道路结构下沉,在背风面近地面处有小的逆时针旋涡生成(工况2,7,8),造成该处污染物浓度较工况1升高。随着机动车道路结构下沉深度增加(工况1,2,7,8),机动车道内逆时针旋涡结构尺寸增加,造成下沉结构中空气流通不畅,尾气污染物在机动车道内逐渐积累,这也是下沉式机动车道内空气污染严重的原因,会对机动车驾驶员的呼吸环境造成较大危害。此外,对于工况7两层道路结构,下层除了机动车道位置形成一个逆时针旋涡结构,污染较为严重外,机动车道两侧空间也形成左侧顺时针、右侧逆时针的涡旋结构,由于空间闭塞,空气流动速度基本为0,污染物浓度水平较高。对于工况9,抬升型道路结构,机动车道的抬升有利于污染物的迅速扩散,因此,机动车道的污染浓度水平较下沉式结构低;但上升的道路结构使得街道背风面近地面人行道路处产生尺寸较大的逆时针旋涡,造成上风向扩散来的尾气污染物在该处聚集,污染物浓度水平较其他情况都高,对该侧行人健康造成不利影响。
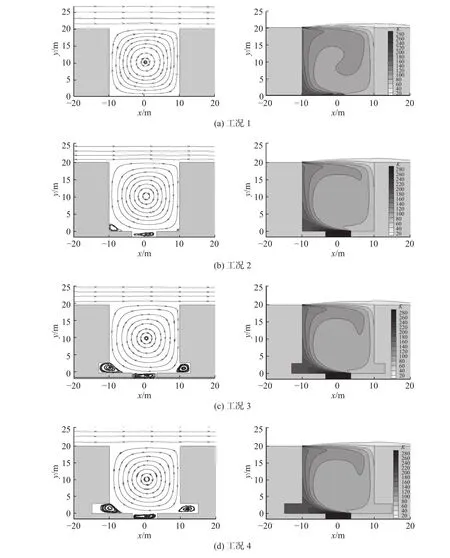
图3 不同截面形态的城市街谷内的速度流线图和无量纲浓度分布Fig.3 Streamlines and distributions of the pollutant dimensionless concentration in the street canyon under different working cases
其次,研究街道峡谷两侧建筑廊道高度和深度变化对街道峡谷内空气流动与污染物扩散的影响。工况2~6均为下沉1.7 m道路结构,但两侧建筑中廊道的高度和深度不同。从图3可知,廊道高度和深度的变化不会对街道峡谷内的流动结构产生影响,即工况3~6在街道峡谷内的流动结构与无廊道的工况2基本相同,因此污染物浓度的分布也基本相同,即廊道结构不会改变街道峡谷主体区域内的污染物浓度分布情况。另外,除了主涡,街道两侧廊道内也会形成左侧逆时针、右侧逆时针的旋涡,而廊道结构尺寸直接影响旋涡的大小。虽然右侧廊道有旋涡产生,但由于主涡的影响使得右侧污染物浓度较低,因此右侧廊道内污染水平较低;左侧廊道正好相反,空气流通不畅,污染物在此聚集,污染物浓度水平较高。
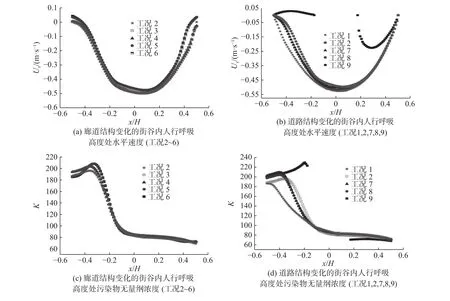
图4 不同工况条件下人行呼吸高度水平速度及污染物无量纲浓度分布Fig.4 Distributions of velocity and dimensionless concentration on the respiratory plane under different working cases
为了进一步分析机动车道路结构及两侧廊道对街道峡谷内行人健康的影响,图4中给出了9 种不同街道截面形态下行人呼吸高度处(y = 1.5 m)流速和污染物无量纲浓度分布。首先,由图4(a)可知,工况2,3,4的速度曲线几乎重合,这说明廊道较低时,与没有廊道相比,对人行呼吸高度流速的影响几乎可以忽略,且此时廊道深度也对流动没有影响,主要是由于廊道较低时其内部涡结构大小与深度无关。随着廊道的增高,廊道内涡结构逐渐变大,与没有廊道相比,街道两侧人行呼吸高度处流速变化愈加明显。从图4(b)可以看出,机动车道路下沉深度对背风侧人行呼吸高度流动变化影响较大,相同深度的结构,流速分布相同(如工况7和8),但对迎风面侧基本没有影响。工况9抬升型道路对两侧人行呼吸高度流速影响较大,因为道路结构阻碍了水平流速,在街道左侧近地面产生较大的二次旋涡。工况9由于是抬高为1.7 m的抬升型道路,上升型道路阻碍了水平流速,而人行呼吸高度处的速度是提取街道峡谷中1.5 m处水平上的速度,因此其人行呼吸高度处的速度只分布在车道的两侧,车道中间没有呼吸高度的水平速度。
从图4(c)可知,街道两侧廊道尺寸对迎风面侧人行呼吸高度污染物浓度分布没有影响,对于背风面侧人行呼吸高度污染物浓度分布略有影响,主要表现在廊道高度的影响。廊道内污染物浓度分布受廊道高度的影响较大,其人行呼吸高度处背风侧附近污染物浓度值相对参考工况增加大约5%。从图4(d)可知,下沉式道路的深度对迎风面侧人行呼吸高度污染物浓度分布也几乎没有影响,但对背风侧人行呼吸高度污染物浓度分布影响较大。随着机动车道下沉深度增加,人行呼吸高度处污染物浓度会随之增加(工况1,2,8)。工况9由于抬升型道路结构的影响,在街谷左人行道内形成一个相对较大的逆时针旋涡,导致污染物在该处不容易扩散而在此累积,因此,工况9背风侧的人行呼吸高度水平处的污染物浓度比其他工况的都大。工况9由于是抬高为1.7 m的抬升型道路,而人行呼吸高度处的浓度,提取的是街道峡谷中1.5 m处水平上的浓度,受抬升型道路的阻碍,其人行呼吸高度处的浓度只分布在车道的两侧。
由图5(见下页)可见,顺时针主旋涡作用下,背风面附近的污染物浓度比迎风面的高,其值约是迎风面附近浓度值的2~3倍。不同工况污染物浓度在迎风建筑物背风侧近地面附近处达到最大,最大值约是迎风面污染物浓度最大值的2.5倍,不利于该侧行人和居住人群的呼吸以及室内外空气的交换。工况1和工况2污染物浓度在背风面附近处变化不大,这是由于在顺时针大旋涡的作用下污染物向背风面迁移所致。由于下沉式道路结构的影响,工况2迎风面附近的污染物浓度值要小于参考工况。工况3和工况4污染物浓度在背风面和迎风面附近分布曲线相似,工况5和工况6无量纲浓度曲线分布也类似,受廊道结构的影响,4个工况在背风侧附近的近地面处浓度变化较大。工况7和工况8在背风面沿高度方向污染物浓度分布变化不大。由于抬升型道路结构的影响,工况9在左侧人行道内形成了一个逆时针旋涡,从而导致在街谷背风侧的污染物浓度比较高。而迎风面,带廊道的工况无量纲浓度沿高度变化不大,道路结构变化的工况无量纲浓度沿高度变化则较大。工况1~2,工况7~9在迎风侧近地面附近处的污染物浓度相差也比较大,而在建筑物最高处浓度相近且达到最低,也可表明迎风面污染物浓度分布受道路结构影响较大。
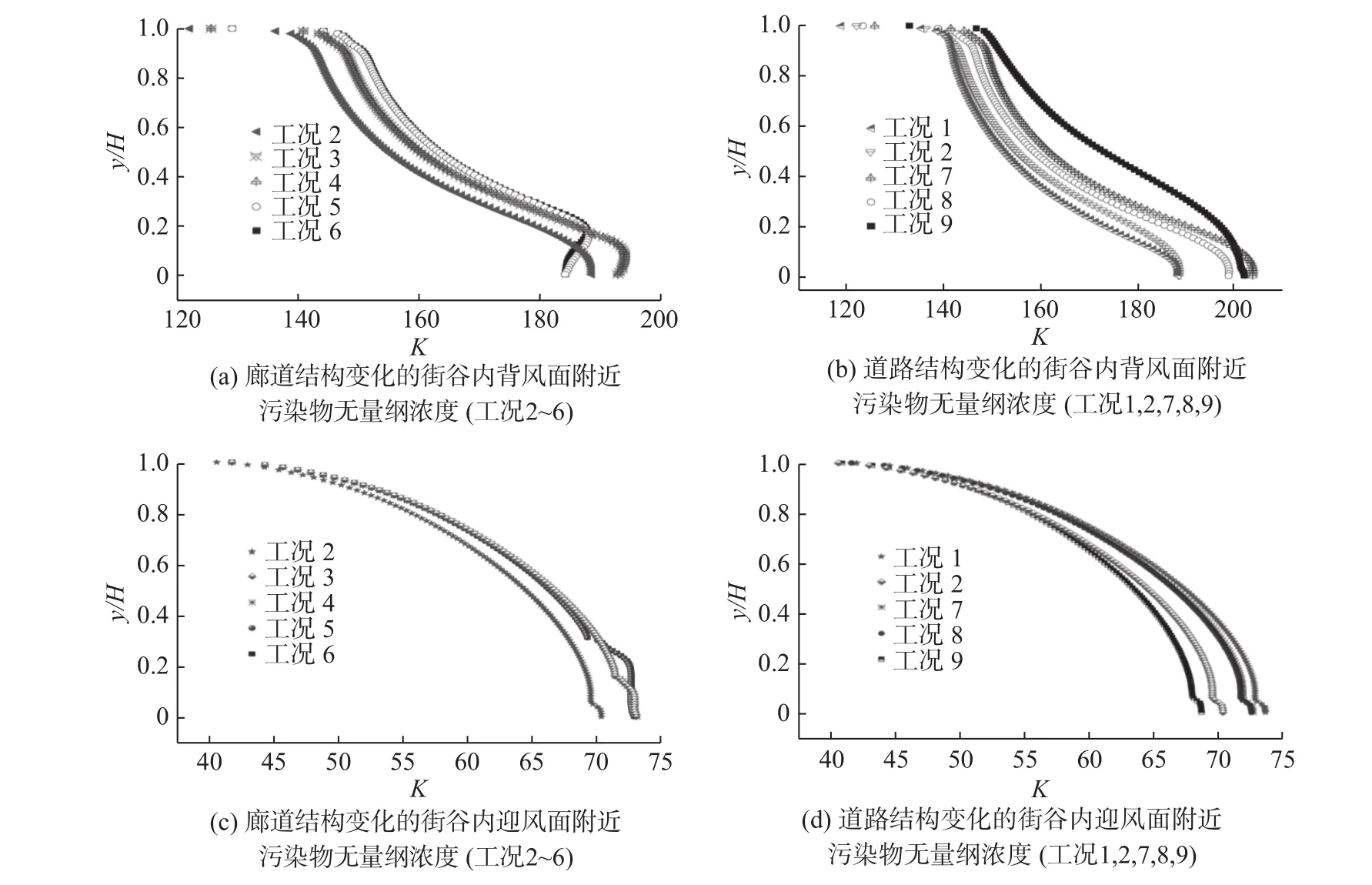
图5 廊道结构变化和道路结构变化的街谷内背风面、迎风面无量纲浓度Fig.5 Dimensionless concentration profiles near the leeward and windward surfaces
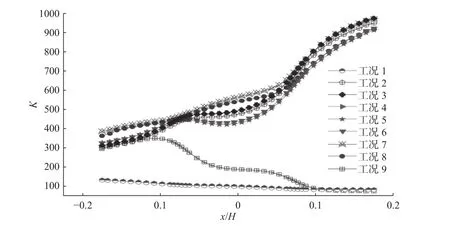
图6 不同工况机动车道内高度1 m处水平方向的污染物无量纲浓度分布Fig.6 Dimensionless distributions of pollutant concentration along the horizontal direction of 1 m height in the vehicle lane for different cases
图6 给出了不同工况机动车道内高度1 m处水平方向的(机动车驾驶员呼吸高度)污染物无量纲浓度分布情况。首先工况1机动车道污染水平最低,且污染物浓度在峡谷两侧的分布比较均匀。这主要是由于街道峡谷内主涡的影响,且检测位置距离主涡涡心位置较远,通风条件较好,污染物可以及时扩散。工况2~8,机动车道污染物浓度均呈现“左低右高”的趋势,主要是受下沉式机动车道内逆时针旋涡的影响,污染物向右侧车道迁移;车道内小的旋涡结构造成空气流通不畅,污染物在此累积。从图中可知,工况2~6中机动车道内污染物浓度水平相当,说明街道两侧廊道结构对下沉式机动车道内污染水平影响不大。对于工况2,7,8,随着下沉式道路深度加深,机动车道污染程度进一步增加;工况7和8由于下沉深度相同,机动车道污染水平相当。工况9抬升型机动车道,检测位置处污染物浓度呈现“左高右低”的趋势,这主要是受街道内顺时针主涡结构的影响,但其污染物浓度较工况1偏高是由于右端抬升结构阻碍由右及左的水平流动,造成机动车道位置处空气流动减缓,不利于污染物的扩散。
4 结 论
本研究基于二维不可压缩流动的Navier-Stocks方程、污染物组分输运方程及标准k-ɛ湍流模型,获取所构建模型的数值解。采用验证的模型参数,构建了9种2类H/W为1的二维城市街道截面形态构造,在来流平均风速为3 m/s情况下,模拟研究了不同城市街道截面形态对街谷内流动结构和污染物分布规律的影响,结论如下:
a. 下沉式道路结构不会改变街道峡谷内主涡结构和污染物分布;下沉式道路结构随着下沉深度的增加,机动车道内污染程度将进一步加重,且受机动车道内涡旋的影响,右侧车道污染程度高于左侧车道。
b. 廊道内污染物浓度分布受廊道高度的影响较大,其人行呼吸高度处背风侧附近污染物浓度值相对参考工况增加大约5%,受廊道高度的影响背风侧附近廊道内及近地面人行道处污染物浓度会比较高。

