多目标多周期多阶段逆向物流网络动态联建

姜芳，郭健全

（1. 上海理工大学，管理学院，上海 200093；2. 上海理工大学，上海−汉堡国际工程学院，上海 200093）

哥本哈根全球气候大会提出了低碳概念，此后，一场关于低碳经济的风暴席卷全球[1]。在物流方面，低碳供应链[2]应运而生。各国政府纷纷响应政策，采取措施来减少碳排放[3]。中国政府进一步加大低碳城市的宣传力度，通过调整政策，加大对非低碳试点城市和欠发达城市的扶持力度，进一步理顺低碳发展与经济建设和环境保护的关系[4]。学者研究了低碳物流的绩效测量系统和策略来减少碳排放，改善环境和市场竞争力[5]。运输业是支撑经济社会活动的重要行业，它的碳排放量占我国碳排放总量的四分之一左右[6-7]，因此，控制运输过程中的碳排放量变得越来越重要。

Guo等[8]考虑到碳排放因素，为上海生鲜电商设计了正逆向物流网络且优化了配送路径；曹锋等[9]以成本最小化为目标，考虑了碳排放，对多周期医药逆向物流网络进行联建研究；Liu等[10]为上海服装电商企业设计了一个多周期逆向物流网络动态联建与优化策略模型，使总成本最小。上述文献大多是企业自建逆向物流网络或是政府单一主导的逆向物流网络，没有考虑到政企结合具有分工明确、优势互补、降低成本、提高效益等优势[11]，因此，本文将政企结合运用到逆向物流网络设计中。

在“互联网+”背景下，凌旭等[12]为废旧手机的回收再利用问题设计了逆向物流网络成本最小模型；翁朝旭等[13]基于B2C模式研究了电商企业逆向物流网络联建策略；黄玉兰等[14]考虑到可持续性发展，为问题药品的召回设计了医药逆向物流网络。上述研究只考虑了单周期单阶段模型，也没有为逆向物流网络设计多目标求解问题，因此，为减少系统不确定性风险，本文研究多目标多周期多阶段逆向物流网络联建模型，以此来优化不同资源的投入。

2013年我国共回收废塑料2 800万t，经过再生利用后，相当于节约石油2.16亿t。国内的废塑料回收率，由2010年以前的约20%上升至2014年的30%以上[15]。近年来，逆向物流研究大多关注经济效益而忽视社会效益[16-17]，塑料具有耐腐蚀、不易分解等特点，对环境造成潜在危害，但有效回收利用，不仅可以减少经济成本，而且有利于提高社会效益，保护环境。因此，为废旧塑料制品的回收再利用设计逆向物流网络具有较强的现实意义。

基于上述分析，本文在碳交易背景下，为上海市废旧塑料制品回收和再利用构建了一个多目标多周期多阶段政企结合逆向物流网络模型，该模型不仅研究了系统运作成本最优、各阶段资源优化等经济效益问题，还研究了降低环境负面影响等社会效益问题。同时，采用遗传算法与粒子群算法，对比验证了模型的有效性。

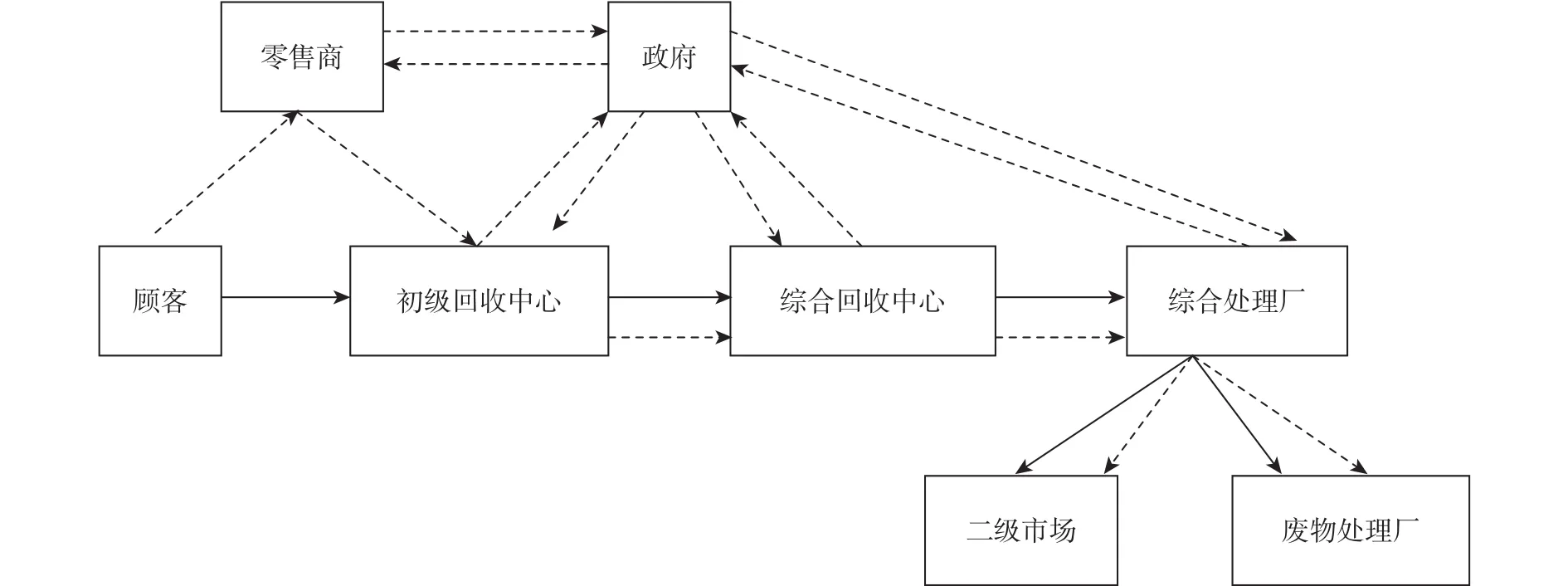
图1 碳税下多目标多周期多阶段政企结合逆向物流网络动态联建模型图Fig.1 Dynamic joint model of the multi-objective multi-period multi-stage government-enterprise reverse logistics network

1 多目标多周期多阶段逆向物流网络动态联建模型

1.1 模型结构分析

图1展示了多目标多周期多阶段逆向物流网络动态联建模型中的8元素，实线代表实物流，虚线代表信息流。

现对具体运营流程及各节点加以说明。

顾客：购买塑料制品，并将损坏或废旧塑料制品通过零售商返回给初级回收中心的消费者。

零售商：向顾客售卖塑料制品，收集顾客返回废旧塑料制品信息并反馈给初级回收中心；接受政府反馈信息，确定产品定价与回收类型，并将结果告知给政府。

政府：接受初级回收中心、综合回收中心、综合处理厂反馈信息，根据这三地信息汇总，与零售商进行协商，确定售卖与回收塑料制品的定价与类型。

初级回收中心：接受零售商反馈信息，接受顾客返回产品，根据政府处理规定，进行简单处理，将产品与信息共同返回给综合回收中心，并将处理结果告知政府部门。

综合回收中心：接受初级回收中心信息与产品，根据政府处理规定，进行综合处理，将产品与信息共同返回给综合处理厂，并将处理结果告知政府部门。

综合处理厂：接受综合回收中心信息与产品，进行深度加工处理包装，根据政府处理规定，能继续出售的产品送往二级市场，严重损坏或有危害的产品运往废物处理厂，并将处理结果告知政府部门。

二级市场：接受综合处理厂产品并继续售卖。

废物处理厂：接受综合处理厂退回品，进行深度处理。

碳排放量：回收过程中车辆产生的二氧化碳总量[18]。

1.2 数学模型

模型基本假设：

a. 废物处理厂的数量和位置是已知的。

b. 候选初级回收中心、综合回收中心、综合处理厂的最大处理能力已知。

c. 候选初级回收中心、综合回收中心、综合处理厂的数量和位置已知。

d. 回收的塑料制品只可以从初级回收中心开始传送，而回收信息从零售商处开始传递。

e. 运输成本与数量的距离成线性关系，节点间的信息成本与数量和距离也成线性关系。

f. 单周期时长为1年，多周期系统中一个周期时长为6个月。

g. 根据实际情况，每阶段的时长可能会发生变化。

h. 各物流节点碳排放量远小于运输过程中碳排放量，故本文只考虑运输过程中碳排放量。

模型中参数如下：

fit，fjt，fpt为初级回收中心、综合回收中心、综合处理厂在周期t中的固定费用。mi,mj,mp为初级回收中心、综合回收中心、综合处理厂在每一个周期后的维修费用。ai,aj,ap,as,ak为每一个对应节点的最大处理能力。ei,ej,ep,es,ek,er,eg为每一个对应节点的综合信息处理成本。ui,uj,up,uk为初级回收中心、综合回收中心、综合处理厂、废物处理厂的综合处理产品成本。α,β,γ为废弃率、二手率、未加工率。dci,dij,djp,dps,dpk,dcj为两节点间的距离。tci,tij,tjp,tps,tpk为两节点间的综合运输成本。ntci,ntps,ntij,ntjp,ntpk,ntjs,ntjk为 t周期内两节点间产品数量。nti,ntj,ntp,nts,ntk,ntr,ntg为 t周期内节点间信息处理数量。Ecar为单位距离上碳排放量。Q为零售商所拥有的碳配额。E为单位碳排放权交易价格。

决策变量如下：

Xti,Xtj,Xtp表示若在 t周期内，初级回收中心i，综合回收中心j，综合处理厂p被选择，则Xti,Xtj,Xtp的取值为 1；否则取值为 0。

基于上述分析与假设，建立数学模型。

第一阶段目标函数为逆向物流网络经济成本CE。

回收产品处理成本

交通运输成本

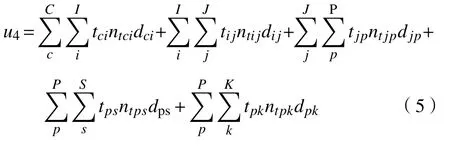
碳交易成本

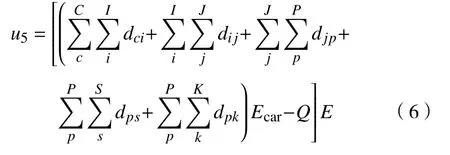
第二阶段目标函数为社会成本CS。

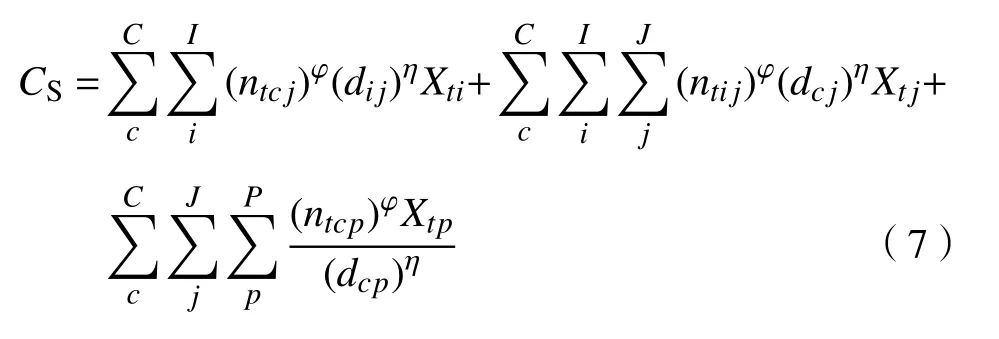
φ

通过层级分析法来测算目标函数的权重，同时测算经济效应系数，为不失一般性，设置 和η的参数值为1，同时通过系数将2个目标函数转换为一个单目标的函数。

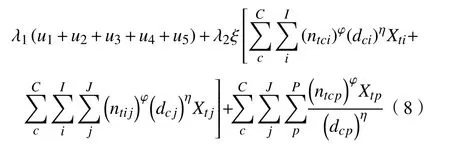
限制条件：

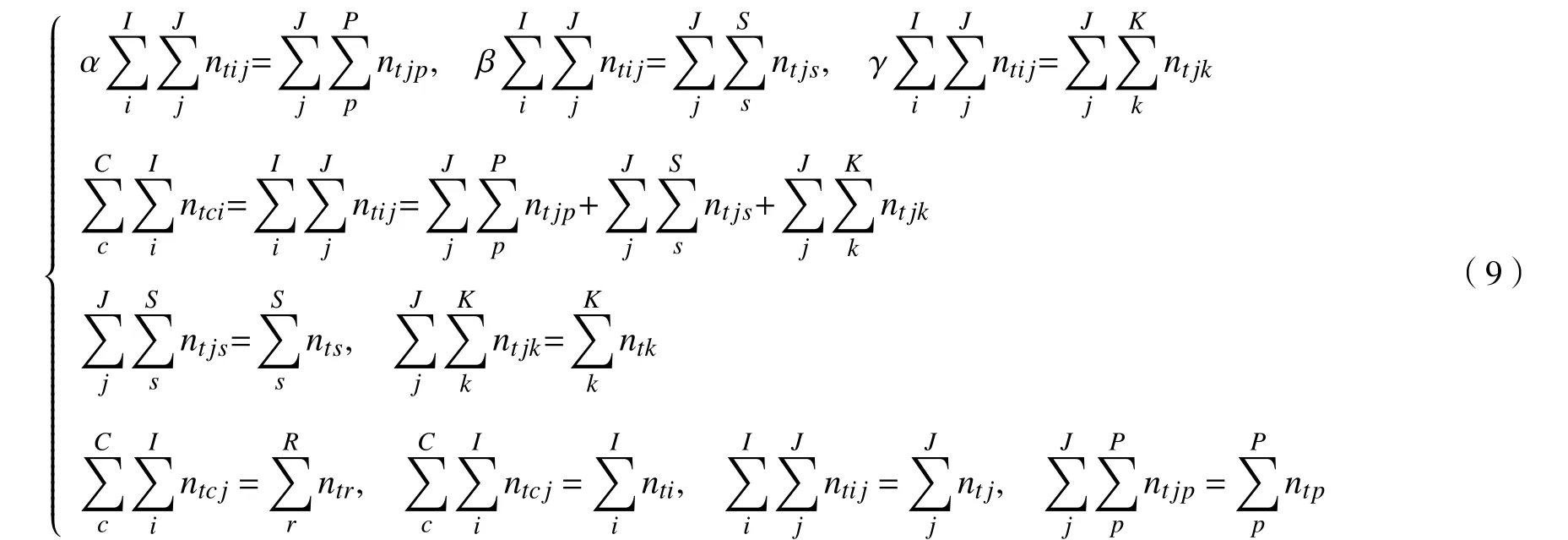
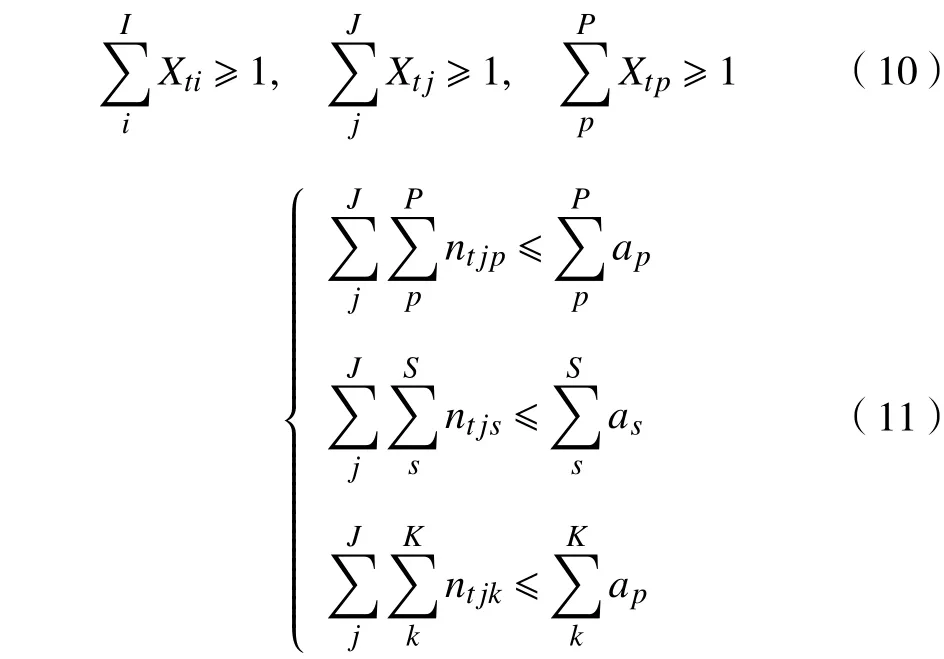
式（1）代表逆向物流网络经济成本，式（2）～（6）分别代表建设成本加维修费用、信息处理成本、产品处理成本、交通运输成本以及碳交易成本。式（7）表示社会成本，第一部分和第二部分表示初级回收中心、综合回收中心与顾客区域之间距离成正比例关系，第三部分表示回收产品的数量成正比例关系，与回收距离成反比例关系。式（8）是将上述目标函数转化为一个单目标函数。式（9）表示实物的流量平衡以及信息的流量平衡。式（10）表示初级回收中心、综合回收中心、综合处理厂至少要各选择一个节点。式（11）表明每个对应节点的回收产品数量低于它们各自的最大处理能力。

2 算法介绍

2.1 遗传算法

遗传算法（GA）通过模拟生物在自然界中不断进化，逐渐适应其生存环境，来获得问题的近似最优解[19]。遗传算法具有全局搜索、高效、智能、并行等特点，被广泛用于解决各种寻优问题，如运输调度、设施布局、网络构建等[20-22]。因而本文运用遗传算法为网络构建问题提供可靠的依据。

遗传算法的主要编写过程。

步骤1 初始化。遗传算法搜索过程中自动确定初级回收中心和综合回收中心以及综合处理厂的基本位置和数量，清理所有干扰因素。

步骤2 适应度评估。适应度值大小决定个体好坏。在满足式（8）～（11）的情况下，利用目标函数式（1）和式（7）来研究最优解决方案。在第一阶段的迭代过程中，使得目标函数（式（12））的值最小，确定初级回收中心和综合回收中心的位置和数量。

第一阶段目标函数：

步骤3 初级回收中心被标注为i=（i/选择的初级回收中心I），综合回收中心被标注为j=（j/选择的综合回收中心J）

步骤4 选择和交叉。选择操作避免遗漏，提高全局收敛性。在满足式（8）～（11）的情况下，利用目标函数式（1）和式（7）来研究最优解决方案。在第二阶段的迭代过程中，使得目标函数（式（13））的值最小，确定综合处理厂的位置和数量。

第二阶段目标函数：

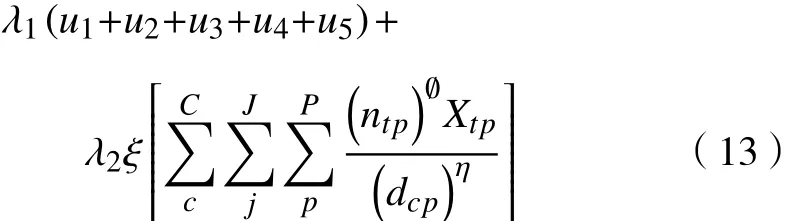
步骤5 综合处理厂被标注为p=（p/选择的综合处理厂P）

步骤6 变异。交叉算子可能使解陷入局部最优，变异算子以较小的概率随机改变串结构中某个串的值，保持种群多样性。将两种操作相结合才能保证遗传算法全局和局部搜索能力。

步骤7 终止规则。如果算法达到预先设定的进化代数，终止算法；否则，转入步骤2。

2.2 粒子群算法

粒子群算法（PSO）是基于进化思想的群体智能优化算法[23]，具有快速收敛获取高质量解的特点，因此，在物流网络设计方面得以应用[24-25]。本文也采用粒子群算法进行网络优化。

粒子群主要编写过程。

步骤1 随机初始化一组粒子（假设粒子规模为M），初始化参数包含粒子速度和初始位置信息。

步骤2 根据适应度函数式（1）和式（7）分别得出所有粒子适应度值。

步骤3 纵向比较每个粒子，若目前粒子适应度值比它得到过的最好位置Pbest更优，则将当前粒子位置设定为最好位置Pbest。

步骤4 横向比较每个粒子，若粒子适应度值比整个粒子群所经历的最好位置gbest更优，那么，gbest的参数值重新设置为当前粒子参数。

步骤5 依靠变异方程改变所有粒子的速度及其位置参数。

步骤6 若满足终止条件，停止程序并输出结果；否则，转向步骤2。

3 算 例

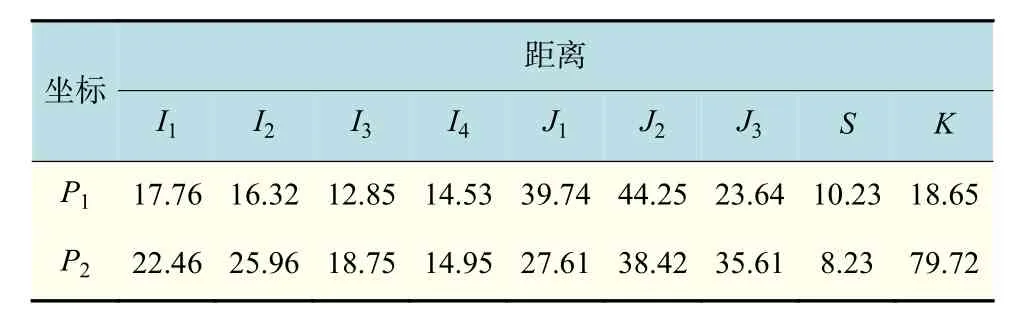
表2 综合处理厂P点的坐标位置与其他节点之间的距离Tab.2 Coordinates of the comprehensive treatment plant P and the distamces between it and other sites km

表3 T周期内回收产品数量Tab.3 Quantity of recovery goods in period T t

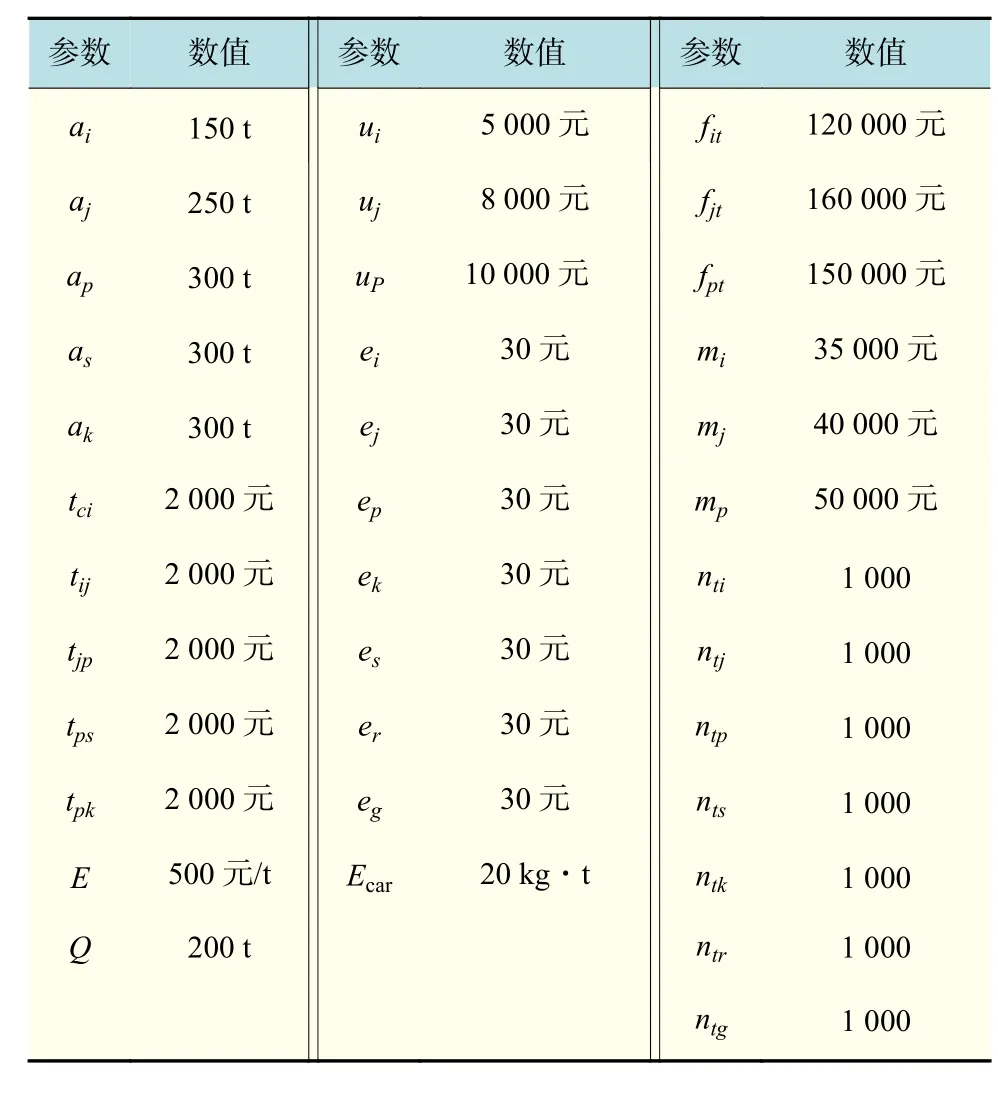
表4 参 数Tab.4 parameters

4 计算结果

遗传算法的计算结果如表5和表6所示。

表5 单周期/多周期计算结果（GA）Tab.5 Computation results by single-period/multiperiod models(GA) 元

表6 单阶段/多阶段计算结果（GA）Tab.6 Computation results by single-stage/multistage models(GA) 元

粒子群算法的计算结果如表7和表8所示。

表7 单周期/多周期计算结果（PSO）Tab.7 Computation results by single-period/multiperiod models(PSO) 元

表8 单阶段/多阶段计算结果（PSO）Tab.8 Computation results by single-stage/multistage models(PSO) 元

单周期与多周期网络位置分布图如图2～4所示。

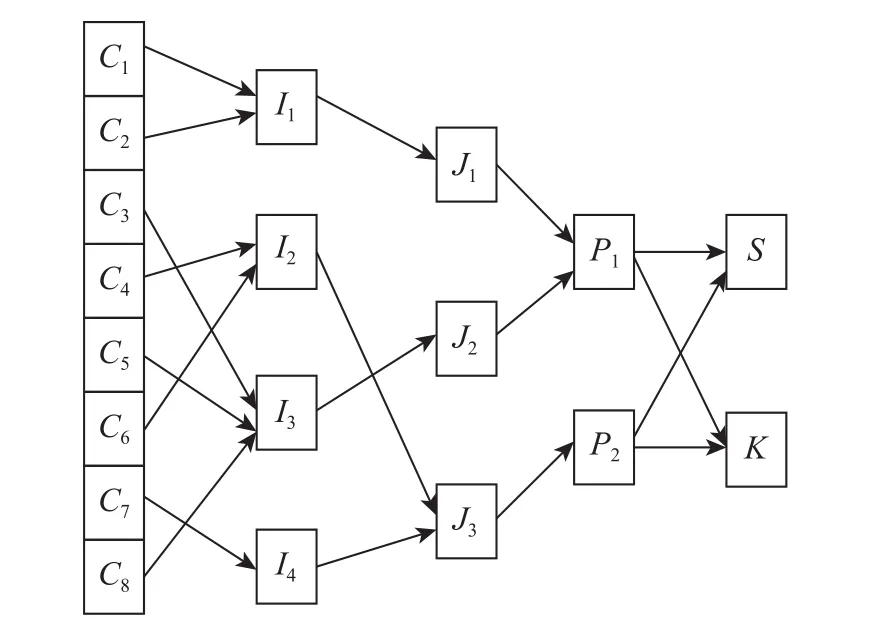
图2 单周期位置分布Fig.2 Position distribution by the single-period model

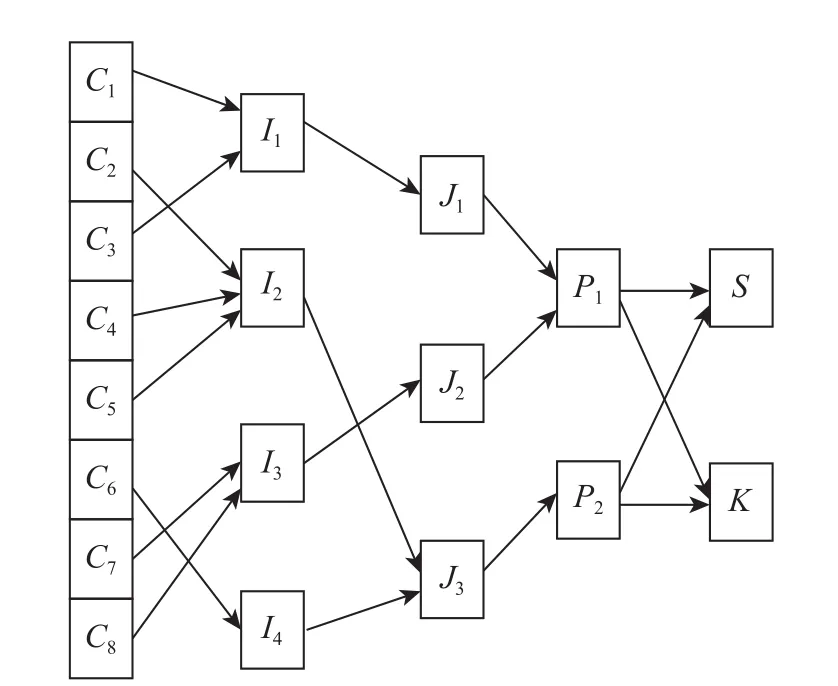
图3 多周期位置分布（GA）Fig.3 Position distribution by the multi-period model(GA)

图4 多周期位置分布（PSO）Fig.4 Position distribution by the multi-period model(PSO)

计算结果表明：

a. 由于回收废旧塑料制品数量的多样性，节点的位置在多周期系统中是动态变化的，而在单周期系统中是固定不变的，多周期系统更符合现实情况。

b. 计算结果显示，多阶段、多周期结果在一定程度上优于单阶段、单周期结果，由于多周期、多阶段状态下投入的资源、节点间的位置和数量的安排可以人为调整与控制，这不仅可以减少系统的不确定性风险，而且在整个操作过程中优化人力和资源的投入。

c. 遗传算法计算的单周期最低成本为 5 277 288元，多周期最低成本为5 146 520元。粒子群算法计算的单周期最低成本为5 276 275元，多周期最低成本为5 145 418元。两种算法的单周期最低成本相对差值仅为0.21%，多周期最低成本相对差值仅为0.22%。同理可证，单阶段最低成本相对差值为0.21%，多阶段最低成本相对差值为0.35%。即基于模型基本假设与约束条件下，验证了模型的有效性。采用两种算法进行对比验证，比单一使用GA/PSO算法或其他算法更能证实结果的可行性。

5 结 论

以最低经济成本、最低碳排放成本以及最小的环境影响程度为目标，构建了以碳交易为背景的多目标多阶段多周期政企结合逆向物流网络动态联建模型来为产品回收问题寻求最优策略，并以上海市废旧塑料制品为例，采用GA和PSO算法，对比验证了模型的有效性。结果表明，该系统模型具有高可行性和稳定性、高效率和低风险等优势，同时多周期优化模型也有助于降低系统的不确定性风险，进一步优化资源的投入。本文为碳交易环境下政企结合逆向物流网络动态联建提供了一个解决方案，也为废旧电子电器产品、废旧电池等具有较高负外部性的产品回收问题提供了借鉴。