基于随机森林的A股股票涨跌预测研究

林娜娜，秦江涛

（1. 上海大学 管理学院，上海 200444；2. 上海理工大学 管理学院，上海 200093）

股票市场研究中，股票涨跌的预测一直是关注的热点。吴微等[1]通过BP神经网络算法对沪市综合指数涨跌情况进行预测，达到了良好的预测精度，但神经网络模型对个股的走势预测效果欠佳。刘道文等[2]采用基于支持向量机的股票选择模型，并以交叉验证法确定了最佳回归参数，并以此建立了预测模型，对上海证券交易所股票价格指数预测效果比较理想，但对于核函数和最佳参数的选取还有提升的空间。戴钟仪[3]运用关联规则，对沪深300指数成分股进行涨跌预测，论证了股票涨跌过程中存在着一定的规律。

经典机器学习算法之一的神经网络算法虽然预测较为精准，但是计算量繁琐。而支持向量机对缺失数据敏感，会极大地影响输出结果，不能适应目前股票预测模型的实际需要。因此，诸多学者建议采用模型组合的方式来提升预测准确度。随机森林算法是一种模型组合，应用到不同的领域上均获得不俗的成果[4-7]。基于随机森林算法的优势，将该算法运用到股票涨跌预测中，能够避免上述预测模型的不足。根据现有文献可知[8-10]，随机森林法预测主要是先对建立的初始指标体系进行筛选，将筛选后的指标数据作为影响变量代入到随机森林中，涨跌情况作为响应变量输出。但现有方法对随机森林本身的模型优化有所欠缺，不能进一步提升预测精确度。

本文在此基础上对随机森林算法进行系统性优化，通过对随机森林中的各项重要参数进行逐步测试，如树节点的变量数（简称：mtry）、树的个数（简称：ntree）、OOB（out of bag）误分率以及变量重要性估计等来提升预测准确度，从而得到预测模型，研究其对股票市场投资决策存在的实际应用价值。

1 指标体系构建

为了建立A股股票涨跌预测模型，首先要确定必要的影响指标作为模型的输入，必要的响应变量作为模型的输出，因为构建股票指标体系是进行后续评价和综合分析的基础。

1.1 初始指标体系建立

吴微等[1]选取成交额、成交量、涨跌幅等股票市场因子作为神经网络研究方法中的指标；国琳[11]等利用4个方面财务因子包括盈利能力、偿债能力、资产营运能力、成长能力运用到股票价格预测中，用实证分析说明其研究的实际价值；谢国强[12]选取股票的开盘价、最高价、最低价、收盘价等市场因子作为支持向量回归机的输入向量，证明该预测模型具有较好的预测精度和泛化能力。但无论是运用股票市场因子或者财务因子作为指标都较不全面，仍有需要改进的地方。

股票的涨跌问题是由复杂因素和环境共同影响导致的，所以本文的初始选股指标体系结合股票市场因子和财务因子共同作为初始指标体系。基于晓雯等[13]和许华丰等[14]对股票指标体系的设计原则，参考其他学者的指标选取，同时剔除了有缺失数据的指标之后，建立以下基本指标体系的初步框架，如表1所示。

表1 初始股票指标体系Tab.1 Initial stock index system

1.2 影响变量与响应变量

以表1中26个指标作为初始影响变量，根据预测模型的未来性，将每只股票下月的涨跌数NMF与0比较，建立响应变量。当NMFi≥0，归为一类，当NMFi＜0归为另一类。其中NMFi是第i只股票下月的涨跌数，n为选取行业的股票数。

2 相关性实证分析

进行相关性分析的100只样本股票，它们的26个影响变量选取时间为2016年6月和2016年7月的月线数据，响应变量选取时间对应为2016年7月和2016年8月月度涨跌情况，其中市场因子和财务因子的数据均来自于东方财富Choice金融客户端和中国证监会指定信息披露的网站：巨潮资讯网。这100只股票皆来自于软件和信息技术服务业，是信息传输、软件和信息技术服务业中的子行业。

2.1 一次筛选——Spearman相关研究

为了通过筛选指标来建立合适的指标体系，达到最终对股票涨跌预测。采用SPSS数理统计软件进行Spearman相关分析，分析每个影响变量与响应变量之间的相关系数，显著性检验选择的是双尾检验。根据得出的相关系数数值大小，从大到小进行排序，如表2所示。

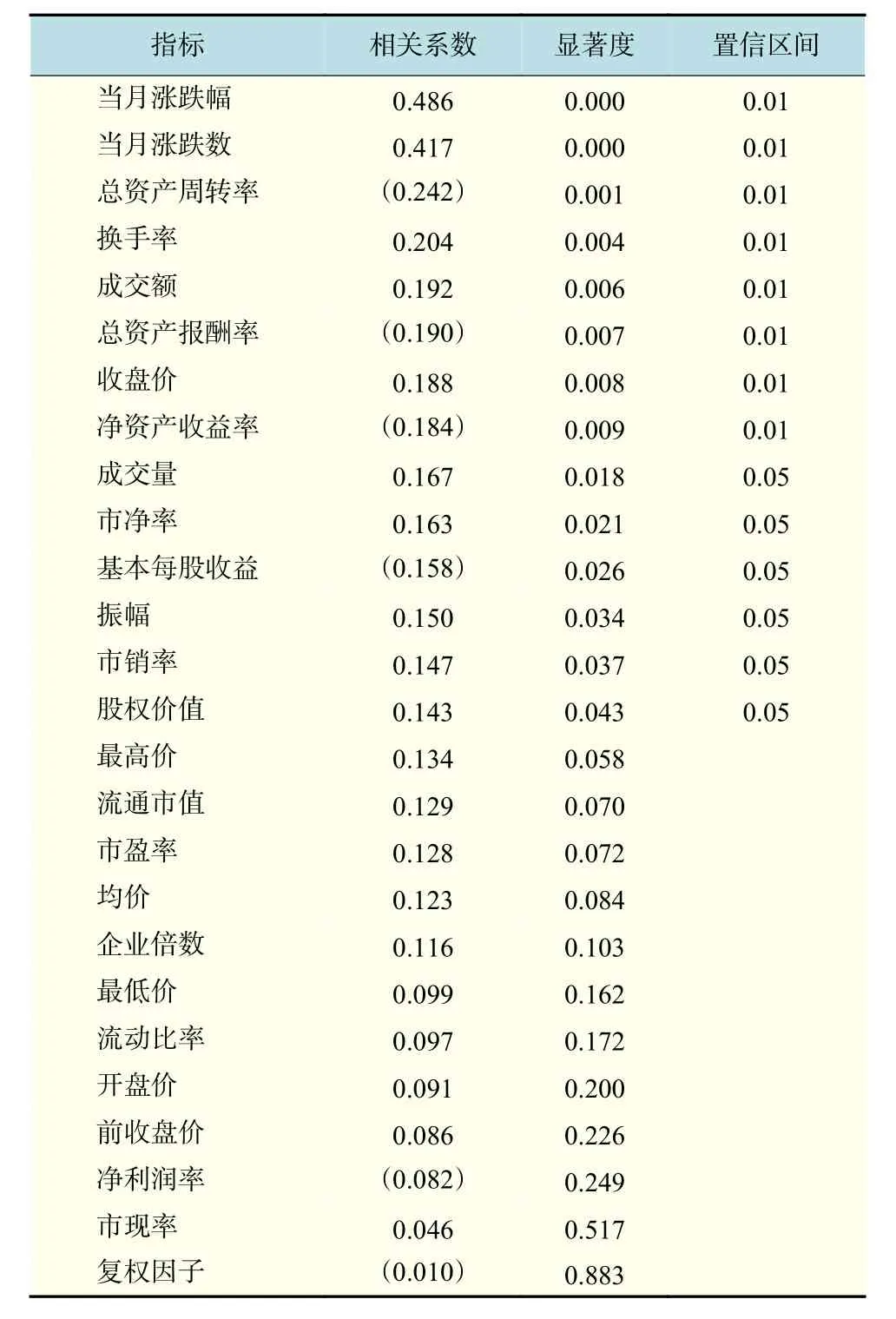
表2 Spearman相关分析结果Tab.2 Spearman correlation analysis results

普遍情况下当显著度数值小于0.05，表明其相关系数数值是可信的，而不是因为样本抽样误差所产生的。通过观察可以发现，显著度小于0.05的前14个指标的相关系数明显比后12个指标来得大。综合考虑各个指标的相关系数大小和对应的显著度，保留前14个影响指标加入到一次筛选后的指标体系中。

2.2 二次筛选——Pearson相关研究

为了保证指标与指标间存在较高的相异性，去除指标间存在显著相关的冗余指标，得到精简的指标体系，从而更进一步优化模型。同样通过SPSS进行Pearson相关分析，分析一次筛选后的14个指标之间的相关系数。显著性检验选择的是双尾检验。去除标准：当两个影响变量之间高度相关时，考量这两个影响变量与响应变量之间的相关系数，舍去相关系数小的，保留相关系数大的。经过二次筛选后的新指标构建了本文的二次筛选13指标体系，如表3所示。

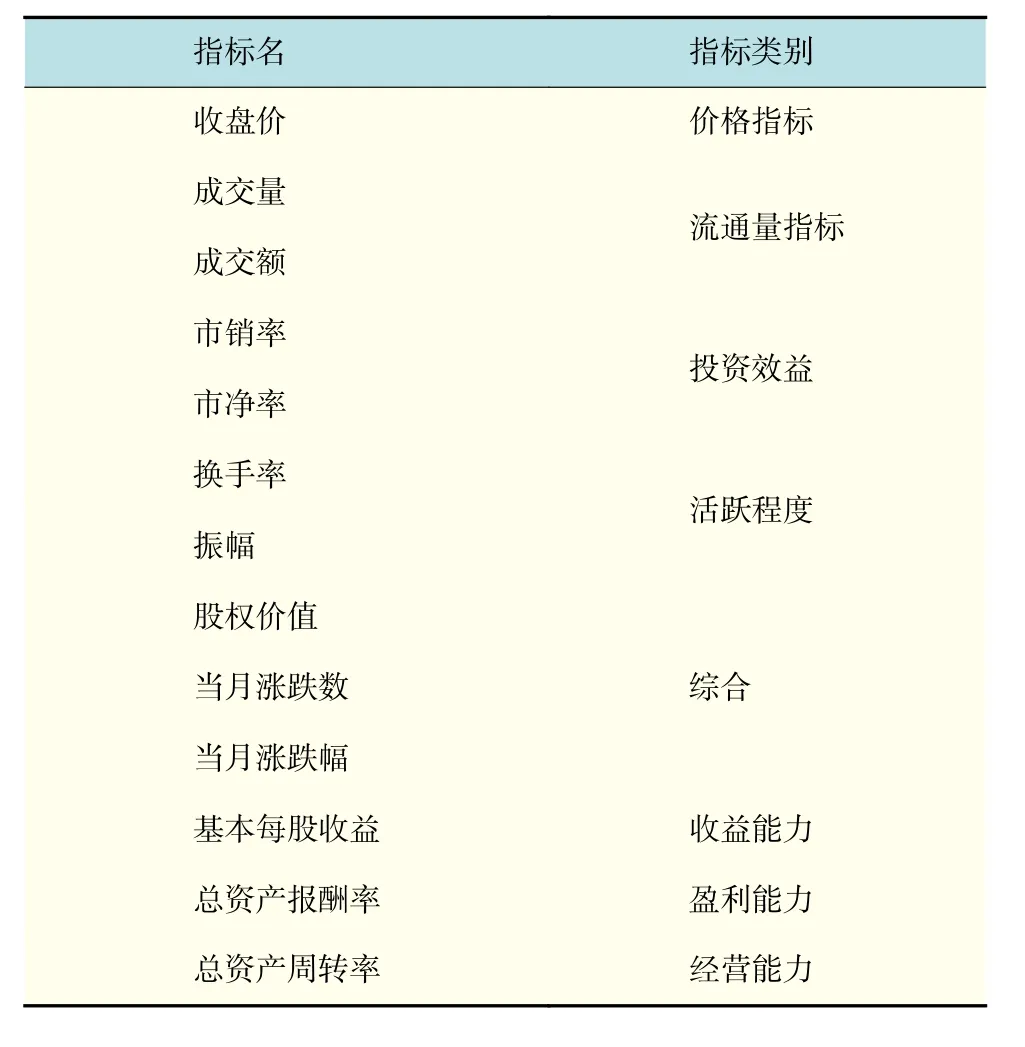
表3 二次筛选股票指标体系Tab.3 Secondary screening of stock index system

3 随机森林实证研究

随机森林算法在样本数据分布不平均、高纬度、存在部分特征缺失的情况下，仍能维持一定的准确度，并且可以在运算量没有明显增加的条件下提升准确度。在处理样本数据时同样表现出较大优势，具备很好的抵抗噪音的能力以及不易陷入过拟合。随机森林参数中的mtry和ntree，可用于协调分类精确性与多样性之间的平衡，OOB误分率可用于对随机森林的泛化误差进行无偏估计，变量重要性估计能够计算每个特征变量对分类结果的重要性。因此，本文在实证研究中对随机森林中的各项重要参数进行测试，以提升预测准确度。

具体研究应用ChiMerge算法对原始数据进行预处理。ChiMerge依赖于卡方分析，如果两个相邻区间的卡方值很低，则表明两者具有非常类似的类分布，那么这两个区间便能够合并；否则，它们应当保持独立，从而达到精确离散化的目的。

3.1 确定随机森林中mtry的值

二次筛选后的指标体系共有13个指标，分别实验得出当mtry为1～13时每次实验的误分率值。为了保证实验结果的有效性，重复以上实验多次，取每个mtry值的误分率均值作为判别mtry合适值的标准。实验结果如图1所示。

图1 OOB误分率均值变化Fig.1 Change of the mean error rate

观察图1可知，当mtry=3时，误■分率达到最低。符合目前的研究[15]，mtry多取为，M为指标总个数。

3.2 确定随机森林中ntree的个数

基于上述确定的mtry=3，对随机森林另一个重要参数ntree进行随机建模，寻求一个适当的ntree。通过实验，图形化展示误分率与树的数量之间的变化关系，如图2所示。

图2 误分率与树的数量之间变化关系Fig.2 Relationship between the error rate and number of trees

观察图2可知，当ntree=200之后，误分率趋于平稳且可以使模型分类精度达到要求。符合目前学者关于随机森林的研究[15]，ntree值皆以大于100棵为合适。

3.3 划分区间数量的测试

区间数量对预测的准确度会有显著的影响。根据实验经验可得，本文的样本数量为200，合适的区间数量为20～29，运用R语言对应当在这个范围内划分多少区间数才能使OOB误分率最低进行研究。在基于mtry=3和ntree=200，再调用经过ChiMerge离散化的2016年6月、7月、8月二次筛选后的13个指标数据，进行随机森林的OOB误分率测试。详细步骤如下：

a. 使用ChiMerge算法对连续性原始数据进行20～29个区间的离散化处理，以下步骤以25区间为例，其他9个区间同理可得。

在R语言中，加载randomForest包，编写语句训练一个随机森林，输出模型的OOB误分率。由于随机森林的随机性，为了保证测试结果的稳定与可靠，同一个实验重复50次，记录每一次的OOB值，如图3所示。由结果可知，划分25个区间时平均OOB误分率的值是26.1%，训练模型的准确率是73.9%。

图3 每个实验的误分率数值Fig.3 Error rate of each experiment

b. 对上述过程做剩余9个区间实验，得出结果如表4所示。

表4 OOB误分率和精确度一览表Tab.4 Model error rate and accuracy list

分析图4可以发现，随着区间数量的变化，随机森林模型的OOB误分率和精确度都在不断变化。随着区间数量的增加，模型的性能有所上升，达到22区间数量时性能最优，精确度达到0.743 3，接着区间数量再增加之后，性能逐渐有所下降。所以，本文选定进行22区间数量划分时会使得随机森林模型的精确度达到最高。

图4 每个离散区间的误分率均值Fig.4 Mean error rate in each discrete interval

4 重要性估计研究

4.1 重要性测试

在最佳22区间数量划分的基础上，对随机森林进行重要性估计测试。本文选用的重要性估计方法是基于Gini分类节点纯度下降量的方法。使用R语言importance（）命令对模型指标进行重要性测试，得到指标重要性结果，如图5所示。

图5 指标的重要性排序Fig.5 Rank importance of indexes

4.2 重要性排序筛选

因为模型的特征变量中不乏噪音指标，这会影响随机森林算法的准确性，所以对每个特征的重要性值进行排序后逐步从重要性最低的开始剔除。目前股票预测中，最低指标数普遍为6个，过少的指标数量会导致模型的可解释性降低和预测结果偶然性的增加。

因此，本文在第一次实验中，筛除重要性最低的ST指标，第二次实验在前一次实验的基础上再筛除PB指标，第三次实验在前两次的基础上再筛除SA指标，依此类推，直到剩下6个指标为止，共实验7次。每个模型为了保证结果的稳定性重复50次，观察实验结果，如下页表5所示。

表5 重要性排序筛选结果Tab.5 Sort results by importance

观察表5可知，进行重要性筛选能使训练模型精确度均值逐渐提高，但到达最大值后又开始减小。所以实验再筛除PS指标的训练模型精确度为0.778 4，是7次实验中最优值。筛选后的指标体 系 包 含 MFR， MF， TAT， CLOSE， SVA，TR和EPS这7个指标，命名为重要性筛选7指标模型。

未经重要性排序筛选之前的最佳精确度均值只有0.743 3，而经过重要排序筛选后的精确度均值提高了3.51%。并且在7次实验中，每一次实验的模型精确度均值皆不同程度高于未经重要性排序筛选之前的精确度均值。由此可见，对随机森林进行重要性估计测试可提升模型精确度。

4.3 不同指标模型的OOB误分率对比

为了使对比结果便于观察，基于研究得出的最佳划分区间22个区间数为基础，对比4个指标模型的50次实验结果，可以得出结果，如图6所示。

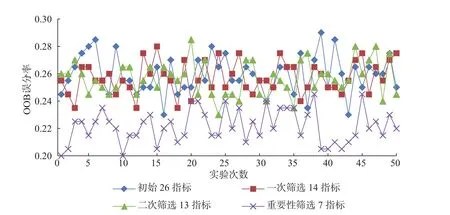
图6 4个指标模型的OOB误分率对比Fig.6 Error rate comparison between four index models

使用SPSS统计软件对4个模型的OOB误分率数据进行描述性统计，结果如表6所示.

表6 4个模型的描述性统计Tab.6 Descriptive statistics of four models

分析图6和表6，可以得出：从模型的OOB误分率来看，一次筛选得出的14个指标整体比初始26个指标的OOB误分率低且更加稳定，表明随机森林在处理高纬度数据方面的优势，可以在一定程度上无需作特征选择；二次筛选的13个指标几乎包含了一次筛选后的14个指标带有的信息量，结果既相近又稳定；重要性筛选7指标模型的OOB误分率比上述3个模型的均低得多，且误分率较稳定。

由此可见，相关性研究大幅度地筛选出了冗余的指标，小幅度地提升了随机森林模型的精确度，在此基础上的重要性估计测试能够在很大程度上提高随机森林模型整体的精确度。

5 股票涨跌预测结果

5.1 随机森林涨跌预测结果

选定重要性筛选7指标模型作为本文的股票涨跌预测模型，将2016年6月与7月的影响变量离散化数据和对应7月和8月的涨跌情况代入到模型中，对随机森林模型进行训练。根据训练之后的模型，将8月所需预测的数据代入，使用randomForest包中的predict（）命令预测出9月股票市场的涨跌情况。

由表7进行统计分析可知，在样本100只股票中，对下月涨跌情况预测的总体精确度达到83%，平均总体涨跌幅为–3.234 17。其中，预测将要上涨的30只股票，预测正确22只，预测精确度达到73.33%，其涨跌幅均值为1.578 04，比总体平均高了4.812 21。预测将会下跌的70只股票，预测正确61只，预测精确度达到87.14%，其涨跌幅均值为–5.296 55，比总体平均低了 2.062 38。从整体来看，该模型的性能优越，对协助投资决策有着实际应用价值。

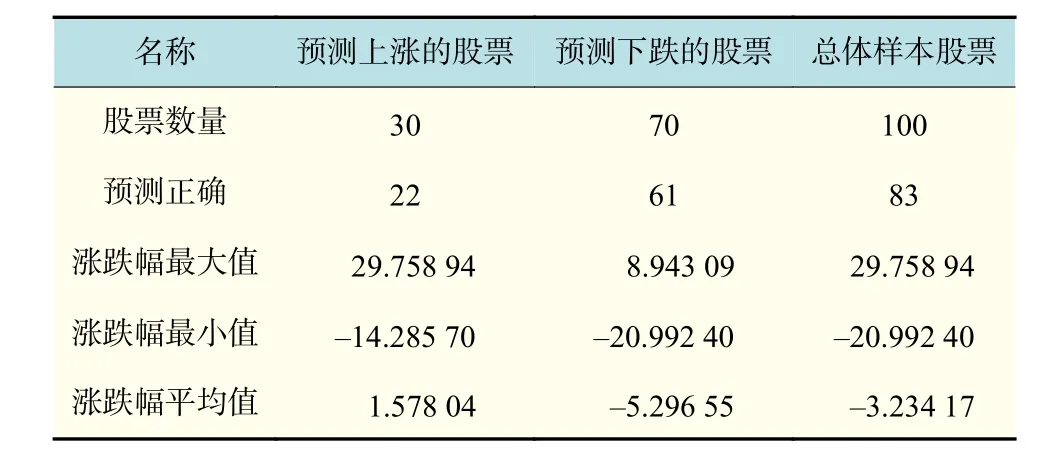
表7 样本股票的预测结果Tab.7 Forecast results for the sample stock

5.2 不同建模方法比较

为了进一步评价随机森林算法建立的模型，本文运用经典机器学习算法之一的二元logistic回归，通过相同的训练样本建立了回归模型，从而来比较不同建模方法所构建模型的预测能力。

通过研究图7可知，随机森林和二元logistic回归对训练模型的预测准确率水平相差不多，随机森林略高于二元logistic回归。但对测试样本进行预测方面，二元logistic回归预测准确度和稳定性明显不如随机森林。随机森林在数据集上表现出很大优势，因为取样随机和特性选择随机的引入，使得随机森林具备很好的抵抗噪音的能力，而且不易陷入过拟合。而二元logistic回归陷入了过拟合，虽然训练数据上能够较好拟合这些数据，但不能对于训练数据以外的其他数据进行很好的预测。

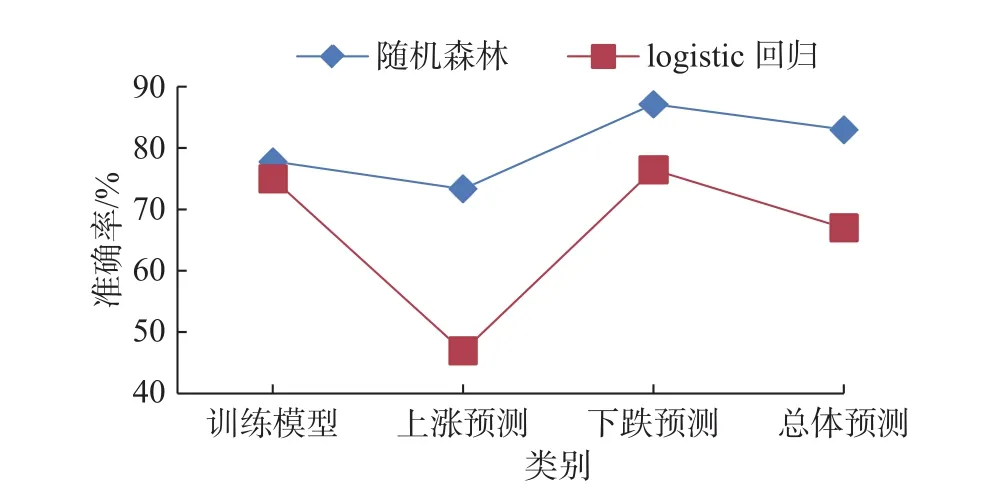
图7 两种建模方法的准确率对比Fig.7 Accuracy comparison of two modeling methods

6 结 论

本文采用机器学习中的随机森林算法以及R语言、SPSS研究工具，对软件和信息技术服务业的100只股票2016年9月的涨跌情况进行预测。

主要通过相关性研究中的Spearman和Pearson方法，对初始指标体系进行筛选，剔除了冗余指标，精简了指标体系。运用ChiMerge算法对指标数据进行离散化，并基于随机森林的重要性估计方法逐次剔除重要性低的指标。最后，通过随机森林和二元logistic回归实证对比证明，随机森林算法的性能稳定且优越。本文建立的随机森林模型在软件和信息技术服务业取得了不错的预测结果，在接下的研究中，作者将继续探究随机森林在其他行业中的普适性，从而进一步论证实验结果。