“量天尺”与牵星板：古代中国与阿拉伯航海中的天文导航工具对比

2018-09-22 02:56陈晓珊

自然科学史研究 2018年2期

陈晓珊

(中国科学院自然科学史研究所，北京 100190)

利用方位星导航是古代航海活动中的主要技术之一，作为观测工具的典型代表，明代《戒庵老人漫笔》中提到的牵星板和泉州湾南宋海船中出土的“量天尺”，其形制、用法、计量单位和技术来源已引发了许多讨论，几乎每个细节中都存在若干种不同看法。*自1966年严敦杰首次发表《牵星术——我国明代航海天文知识一瞥》(《科学史集刊》编辑委员会：《科学史集刊》第9期，北京：科学出版社，1966年，第77～88页)以来，国内主要相关研究成果还有韩振华《我国古代航海用的量天尺》(文物编辑委员会：《文物集刊》第2期，北京：文物出版社，1980年，第217～221页)和《牵星术——十五世纪初有关西亚东非天文航海的记录》(韩振华：《航海交通贸易研究》，香港大学亚洲研究中心，2002年，第532～598页)，袁启书《过洋牵星术考证》(《中国航海》1986年第1期，第71～79页)，刘南威主编：《中国古代航海天文》(广州：科学普及出版社广州分社，1989年)，孙光圻、陈鹰《试论郑和牵星术中的阿拉伯天文航海因素》(郑和下西洋600周年纪念活动筹备领导小组编：《郑和下西洋研究文选(1905—2005)》，北京：海洋出版社，2005年，第587～592页)，赵鹿军《郑和牵星图考释及复原》(《中国航海》1993年第1期，第75～95页)、金秋鹏《略论牵星板》(《海交史研究》1996年第2期，第83～88页)，王玉民：《以尺量天：中国古代目视尺度天象记录的量化与归算》第三章第五节《“指”系统、牵星术及其他》(济南：山东教育出版社，2008年，第64～71页)，陈忠烈《相会在星空——十五至十七世纪东西方的航海天文》(广东省社会科学院历史与孙中山研究所编：《广东省社会科学院历史与孙中山研究所建所五十周年纪念文集》，香港：银河出版社，2008年，第241～258页)，黄盛璋《〈过洋牵星图〉起源阿拉伯与中国发展、提高的贡献指迷解难——创建中国海学新学，复兴中国海国文明研究之一》(刘迎胜主编：《〈大明混一图〉与〈混一疆理图〉研究——中古时代后期东亚的寰宇图与世界地理知识》，南京：凤凰出版社，2010年，第120～163页)等。本文将探讨此前研究中的一些疑问，并初步分析古代中国与阿拉伯航海中天文导航工具的差异及其成因。

1 泉州宋船“量天尺”与明代马怀德牵星板形制考

1974年，福建泉州湾出土一艘南宋海船，船中有一竹尺，由于形制奇特，被认为是中国古代航海时测量天体的专用导航工具，并被称为“量天尺”[1]或“牵星尺”[2]。竹尺出土时残为3段，存有5格刻度，每格长2.6厘米，另有约3格的长度上没有刻度。在早期研究中，它曾被拼为左边一格、右边四格，中间一段无刻格的形制([1]，218～219页；[3])，后又调整为一半有刻度，一半无刻度，有刻度的一半用来度量天体，无刻度的一段用以手持，如图1所示：

图1 《我国古代航海天文资料辑录》中的竹尺形制[2]

早期研究者认为这柄竹尺形态与其他尺子不同，且其每寸长2.6厘米，与传世宋尺的每寸3.165厘米相差较大([1]，218～219页)，又因出土于海船尾部第13舱，为古代舟师工作之处，因此将这柄竹尺与陆上测量表影用的量天尺做对比，认定其为计算纬度的海上专用天体测量工具。然而1975年，福州南宋黄升墓中也出土了一柄形制相似的刻花髹漆木尺，从墓主人身份和随葬物信息可知其为女性裁缝用具，同样是只有一半刻度，刻画五格，另一半无刻格([5]，80～81页；[6])，每寸约为2.8厘米([4]，22页)，与泉州海船竹尺形制相同，长度相近。南宋海船与这座墓葬距离不远，年代相近，由此可推测海船上的半刻度竹尺并非专用的天体测量工具，而是一件普通民用物品。此外《中国古代度量衡图集》中收录十余件仅有一半刻度的古尺，年代从东汉至南宋，这也证明了泉州海船竹尺形制的普遍性。又有《南宋的省尺与乡俗尺》一文，根据《三山记》中淳熙年间赵汝愚的奏疏，证明南宋时福建“乡尺”是27厘米左右的一种短尺(《中国古代度量衡图集》测定泉州竹尺为27厘米([7]，图版说明，8页))，而“官尺”是30.9或31厘米左右的营造官尺，可见泉州沉船里发现的残竹尺正属于福建乡尺[8]。

在竹尺出土的海船第13舱中，同时发现的还有一件铁斧和一件钉送，应当都是船上所用的木工工具([4]，23页)，这柄尺子很可能也是同类用途。由于该尺是目前唯一被认定的中国传统恒星导航工具，也没有其他文献或证据显示有类似工具存在，所以在排除了其专有用途的可能之后，实际上已经没有任何证据能够证明中国古代航海活动中，曾经存在原创的专用天体测量工具与计量单位。

泉州海船上的竹尺之所以在一些研究中被称为牵星尺，是因为明代李诩《戒庵老人漫笔》中介绍了一种名为牵星板的工具，它由如图2所示的一系列共12片方形乌木板组成，书中称收藏者为“苏州马怀德”。1966年发表的严敦杰《牵星术——我国明代航海天文知识一瞥》中首先介绍了这条史料，认为牵星板是中国古代用来测定船舶所在位置地理纬度的航海天文仪器([9]，88页)，并引用晚近时期仍在使用的阿拉伯天文导航工具kamal加以对比，分析马怀德所藏牵星板的使用方法。文中提到两种古代阿拉伯天文导航工具，一种是由一系列木板和绳子组成，另一种是由一块木片和一根穿过木片中央的绳子组成，绳子上打若干绳结，使用时左手执木板，右手拉直绳子，使木板上边缘对准北极星，下边缘与海天连接线相切，可以大约测出所在地北极星距水平的高度，并根据木板宽度和绳长计算海船所在处的地理纬度。

图2 《牵星术——我国明代航海天文知识一瞥》中所绘牵星板图([9]，77页)

这篇文章引起了研究者们对中国古代天文导航中域外元素的关*，但由于文中默认马怀德牵星板与这些域外工具属同一类型，使得此后50年中，许多研究者按此思路出发，形成板绳结合，计算纬度定位的探索模式，认为马怀德牵星板与相关工具一样，也是一种与绳子搭配，并用来测定地理纬度以实现定位功能的工具。然而，回顾《戒庵老人漫笔》中的原始记载，却会看到原文中并未提及牵星板上有绳子，也没有提到板上是否有绳洞。其原文是：

苏州马怀德牵星板一副十二片，乌木为之，自小渐大，大者长七寸余，标为一指二指以至十二指，俱有细刻若分寸然。又有象牙一块，长二尺，四角皆缺，上有半指半角一角三角等字，颠倒相向，盖周髀算尺也。(同书第43页《校勘记》：“‘长二尺’，明藏说小萃本作‘长二寸’，未知孰是。”) ([10]，29页)

如果研究者此前从没有对阿拉伯航海工具的印象，而仅是看这段记载，恐怕绝不会产生“木板的中心有一根绳子”的判断，因为这里并没有任何线索与绳子相关。然而，由于先对相关工具有所了解，所以严敦杰文中在介绍了牵星板之后，认为它的形制应该是：

用十二块方的木板，最大一块每边长约二十四厘米(合明尺七寸七分强)，叫十二指。其次是约二十二厘米，叫十一指。这样每块递减二厘米，到最小的一块每边长约二厘米，叫一指。木板的中心穿一根绳子，这绳子的长度是自眼到手执板间的距离(手臂撑直)，大约是七十二厘米左右。([9]，77～78页)

这里衍生出了关于绳子的阐述，并且将其长度界定为72厘米，但这些细节在李诩的原文中并不存在。然而从此之后，关于牵星板的研究都不免要对“牵星板上是否有绳子”这一问题做出解释，如《略论牵星板》中认为板上本来有绳子，只是李诩看到时绳子已经遗失了([11]，87页)。由于马怀德真实身份未知，由此引发了许多猜测，《中国科学技术史》中提及北宋时有一位同名将领([12]，625页)，《宋史》记载其是北宋祥符(今开封)籍，长期在西北边疆作战[13]，有研究认为此人在老年时移居苏州，牵星板应是他的收藏品[14]。但从《宋史》中的记载来看，并没有证据表明北宋的马怀德曾经到过苏州。

关于牵星板收藏者的身份存在不同猜测，而不同身份带来的知识水平和社会阅历的差异，以及他生活的时代和地区，与李诩的关系，都可能影响到关于牵星板的记载是否可靠。那么马怀德究竟是什么人？再回到《戒庵老人漫笔》中，会看到载有牵星板事迹的同一卷里，还有一条这样的记载：

马怀德言，曾为人求文字于祝枝山，问曰：“是见精神否？”(原*：俗以取人钱为精神。)曰：“然”。又曰：“吾不与他计较，清物也好”。问何清物，则曰：“青羊绒罢。” ([10]，16页)

既然出现在同一本书同一卷中，可以相信这就是李诩提到的牵星板收藏者马怀德。从两条事迹来看，他居住在明朝的苏州，既然与祝枝山、李诩交游，应是和他们生活在同一年代，并具有一定学识和社会地位，所以他对家藏牵星板的介绍，关于其形制与原理的阐述，应当也是较为可信的。他可能与阿拉伯文明有一定联系(马怀德这个名字屡见用于回族人名[*]例如《中国武术大辞典》记载的回族武术家马怀德(《中国武术大辞典》编辑委员会编著：《中国武术大辞典》，北京：人民体育出版社，1990年，第470页。))，这套牵星板也可能来自此前中国与阿拉伯世界的航海交流。相似类型的天文导航工具并非只见于《戒庵老人漫笔》，《马可波罗行纪》中也有两条相关*解如下：

剌木学曾引一随同达迦玛(Vasco de Gama)之弗洛郞司(Florence，今佛罗伦萨)人初次航行之说云：“航行印度海中者不用罗盘，仅恃若干木制之四角规以辨方位，若有云雾而不能见星宿时，航行则甚难也。”

……颇节引一传教师之说云：“印度舵手测量高度之法，用一绳结数结，口啣其一端，绳中横贯一木，如是不难测得小熊星尾，即通称之北斗星或北极星也。”([15]，382页)

*中提到的这两种工具，第一种更像由一系列木板组成、未提及绳子的马怀德牵星板；而第二种更像是由一片木板和若干绳结组成的kamal。此外，严敦杰文中还转述了16世纪阿拉伯航海者所作《印度洋航海记》中的一种设备，其形制特点是“古代用九块板，第一块的长度约为人们的一小指长，把它分而为四，每一段叫一指，即第一块板是四指。这四指刚好是五车二与Dobban星间的距离。其次每一块增一指，以至于第九块为十二指。板的中心有一线，使用时左手执板，右手持线，左手伸直，这样便可通过观测求得所在地的位置。”[*]严敦杰：《牵星术——我国明代航海天文知识一瞥》，第79页。原文译自Sidi Ali, translated by Joseph Von Hammer. Extracts from the Mohit, that is the Ocean, a Turkish work on navigation in the Indian seas, Journal of the Asiatic Society of Bengal.1838: pp.771～772。黄盛璋《〈过洋牵星图〉起源阿拉伯与中国发展、提高的贡献指迷解难》中对原书有所考证，本文将沿用严敦杰文中的译法，将Sidi Ali的这部著作称为《印度洋航海记》。这种板应当是严敦杰文中推测马怀德牵星板使用方法的依据，它看起来像是前两种的结合体，既有一系列木板，也有绳子，但是没有绳结。

2 作为计量单位的“指”代表的角度演变

马怀德牵星板引人关*的原因之一，是其中出现了“指”和“角”两个计量单位。明代航海文献中屡见这类记载，例如《顺风相送》中的《古里往祖法儿》航线：

过礁头开洋，辛戌五十更，看北辰六指三角、灯笼星八指三角；单辛七十更，看北斗七指三角、灯笼星七指三角，取祖法儿马头，水六托，泊船是也。[16]

在《戒庵老人漫笔》的描述中，牵星板“大者长七寸余，标为一指二指以至十二指，俱有细刻若分寸然。又有象牙一块，长二尺，四角皆缺，上有半指半角一角三角等字，颠倒相向”。作为计量单位的指究竟是何种含义？国内相关研究常讨论它是中国原创还是由阿拉伯航海术引入，以及其代表的角度究竟为多少，但一直未有定论，如严敦杰文中认为其数值在1°34′和1°36′之间([9]，78页)，而《航海天文》调研小组则认为1指约相当于1.9°[17]。在这种情况下，如观察阿拉伯航海术中相关概念的形成过程及其含义，对此问题或有可参考之处。

在1836年发表的《关于阿拉伯人的航海仪器》中，介绍了19世纪印度洋周边航海中使用的天体测量工具Kamal，它的计量单位后来被通称为isba。在文章的开头，作者解释了isba一词的含义：一位阿拉伯海员伸直手臂，在地平线上横向并拢自己的手指，用它们计算北极星的高度。根据这种解释，isba其实就是“指”，它是一种粗略的早期导航方式[*]James Prinsep, Note on the nautical instruments of the Arabs,Journal of the Asiatic Society of Bengal, 1836，pp.784～794.这段原文在784页。在这一年，isba还被写作issabah或者issaba，但在1838年之后，它就被固定写作isba了。详见Sidi Ali Celebi, translated by Joseph Von Hammer. Extracts from the Mohit, that is the Ocean, a Turkish work on navigation in the Indian seas, Journal of the Asiatic Society of Bengal. 1836: pp.441～468, 1838： pp.767～780.这篇文章的中文译名《关于阿拉伯人的航海仪器》系沿用孙光圻、陈鹰《试论郑和牵星术中的阿拉伯天文航海因素》中的译法。。

在航海工具kamal上，isba有另一种表现方式。按照文章中记载，这种工具的使用和制作方法是：取一块边长约2英寸的方形木板，将一根绳子穿过木板中心，绳子上打9个结。使用这种工具测量北极星的高度时，观测者用牙齿咬住绳子，木板下缘对准海天连接线，上缘对准北极星(如图3所示)。绳子打结的方式是，首先将木板宽度乘以5倍，在绳子上标记，并将这段绳长作为一个整体，等分为12段，然后在距离木板第6段处打第一个结，称为“12”。再将这段长度为木板五倍的绳长等分为11段，在距离木板第6段的地方也打一个结，称为“11”。以此类推，再分别等分成10，9，8，7和6段，也是在第6段上打结。这样，到等分为6段并打结时，恰好打结在长度为木板5倍的绳长上，这个点称为“6”。然后在此段绳长之外，再延伸出一个木板宽度的地方，打结称为“5”，又在另外延伸出1.5倍木板宽度的地方，打结称为“4”。一般到了这里，打结就结束了[*]James Prinsep: Note on the nautical instruments of the Arabs,p.785: The mode of marking off these knots is curious. Five times the length of the horn is first taken, as unity, and divided into twelve parts: then at the distance of six of these parts from the horn, the first knot is made which is called “12”. Again the unit is divided into eleven parts, and six of these being measured on the string from the horn as before, the second knot is tied and denominated “11”. The unit is thus successively divided into 10, 9, 8, 7, and 6 parts, when the knot tied will of course exactly meet the original point of five diameters: this point is numbered “6”. Beyond it one diameter of the horn is laid off for the “5” division and one and a half again beyond, that for the “4” division, which usually terminates the scale. 《牵星术——我国明代航海天文知识一瞥》第79页在引述这篇文章时，将这段文字翻译为“这木板中心穿一根绳，以木板长度的五倍长，再十二分之，以离板最近十二分之处打一个结，叫十二指。同样长度十一分之，离板最近十一分之一处打一个结，叫十一指。这样一直算到四指。这样，这个绳子上一共打了九个结。(也可以算到一指打十二个结的)”。英文原文中用黑体字标出的部分在这段中文翻译中被遗漏了，实际每次都是等分绳子之后，在第6份上打结。关于这种工具的制作说明，另见Sidi Ali Celebi, translated by Joseph Von Hammer. Extracts from the Mohit, that is the Ocean, a Turkish work on navigation in the Indian seas, 1838: pp.772～773.。这些打结的数字就是isba(指)在kamal上的表现形式。

图3 《关于阿拉伯人的航海仪器》中的kamal([18]，784页附图)

图4 Kamal计算原理示意图([9]，78页)

由于在北半球观察北极星时，其仰角等于观测者所在的地理纬度，所以当绳子垂直于木板时，根据kamal上一系列绳结的位置，就可以用计算余切值的方法测算当地纬度。从图3、4中可知，绳结对应的角度θ是当地纬度的一半，∠AOC的度数等于当地纬度，当木板长度AC为2英寸，绳子的长度OB是板长的5倍时，第N个绳结对应的角度θ的余切值计算过程如下：

Ctgθ=[2(板长是2英寸)×5(绳子是板长的5倍)×6(在第6段上打结)/N(绳子被均分成N段，N=12，11，10……4)]/1(板长的一半是1英寸)

=60/N(N=12，11，10……4)

从图5所示的计算结果中可知，当绳长是板长的5倍时，共打9个结，即4指到12指，可测量的纬度区间是 7°36′到22°38′，每两个结之间的纬度差保持在 1°50′-1°56′，即大约1.9°左右，可以认为近似两个纬度。

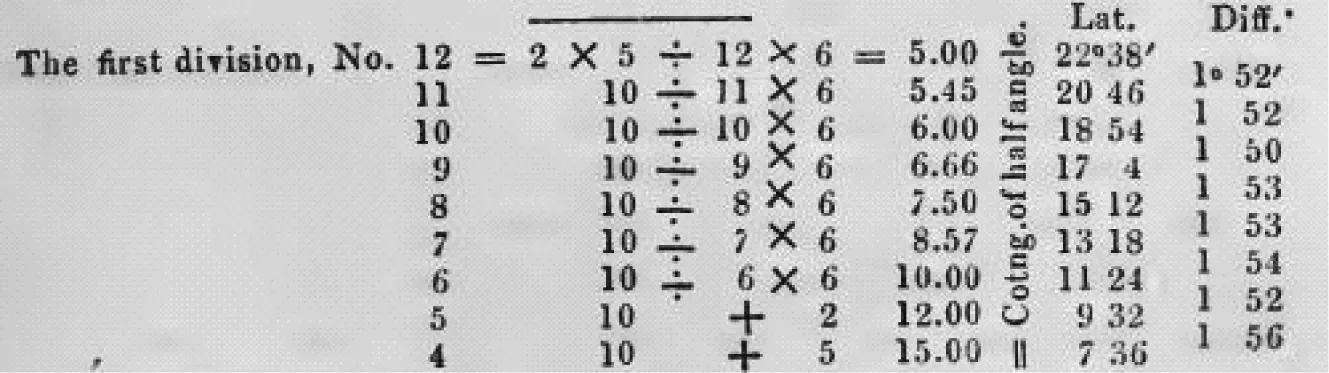
图5 《关于阿拉伯人的航海仪器》中的计算数据(绳长为木板边长5倍时)([18]，785页)

除了这种绳长是板长5倍的kamal之外，《关于阿拉伯人的航海仪器》中还提到了另一种kamal，它与前一种相似，只是绳长从板长的5倍变成了6倍，绳结的数量也从9个结变成了16个结。从图6中可知，这种kamal可测量的纬度区间是1°36′到25°04′，每两个结之间的纬度差是1°31′～1°36′。它的纬度计算方式是：

Ctgθ=[2(板长是2英寸)×6(绳子是板长的6倍)×6(在第6段上打结)/N(绳子被分成N份，N=16，11，10……1)]/1(板长的一半是1英寸)

改进的CLIQUE算法并行化的思想：将算法的并行化分为网格划分和聚类两个阶段，在每个阶段启动1个Job完成网格划分和聚类操作。图6为改进算法的并行化实现流程图。

=72/N(N=16，11，10……1)

图6 《关于阿拉伯人的航海仪器》中的计算数据(绳长为木板边长6倍时)([18]，786页)

Kamal的计算原理表明，它是三角学发展史，尤其是余切或正切函数发展的产物，这种简易工具的原型应与天文数学家制造的测量仪器相关。《印度洋中的阿拉伯导航史》中介绍了这一发展过程：测星高的工具“花剌子模杖”带有刻度，它建立在三角函数的原理基础上，木杖后来被沿间隔打若干结的绳子取代，绳子从木板中心穿过。在夜晚的航船上，可以用这种工具测量星辰在地平线之上的高度[19]。这种工具与阿拉伯数学家阿尔·巴塔尼(852～929)的成就相符，他曾制作了从0°到90°之间每相隔1°的余切表，而kamal赖以计算的每个半角都接近1°。之所以将绳子长度取为木板边长的5倍或6倍，平分成若干段后再分别在第6段上打结，也是出于实际操作需要，人手臂长度有限，要满足等式所需的条件，必须在绳长和绳结位置之间取一平衡点[*]当需要测量的纬度范围较大时，有的kamal会采用一大一小两块木板，分别在不同的纬度地区使用，以解决手臂长度不足的问题。可参考Dennis Fisher, Latitude Hooks and Azimuth Ring, McGraw-Hill Companies Book, Camden, Maine,1995, p.21,以及E.G.R.Taylor, The haven-finding art: A history of navigation from Odysseus to Captain Cook, London: Hollis and Carter, 1956, p.180，图版6。。据介绍，在不同时间和不同地点，isba代表的数值和kamal的形制有所不同。比如在1394年时，它是1°56′，而在1550年时，它是1°33′([20]， 779页)。

由于翻译中遗漏了每次等分绳子后，都要在第6段上打结的信息，严敦杰文中将牵星板的使用方法解释为手持一根72厘米的绳子结合一系列木板使用[*]严敦杰：《牵星术——我国明代航海天文知识一瞥》，第77～78页。原文是：“木板的中心穿一根绳子，这绳子的长度是自眼到手执板间的距离(手臂撑直)，大约是七十二厘米左右……已知眼到木板间的距离是七十二厘米，每块木板的宽度又知道；这样可以通过观测求所在地的地理纬度。”，并计算出1指在1°34′和1°36′之间，近似1550年时isba的数值。而《我国最早记载牵星术的海图》中将持牵星板的手臂长度取为60厘米，并计算出1指的数值约为1.91°，近似1394年时isba的数值。后者认为中国的牵星板是垂直手持的，其计算方式如图7所示：

图7 《我国最早记载牵星术的海图》中的垂直测量法计算原理示意图[21]

需要计算的α是∠SOL，即当地纬度，取最小的1指牵星板边长约2厘米，“对一般的中国人来说，其手臂向前伸直后，母指虎口到眼的距离约为手指宽的30倍(即约60厘米)，则手指张角的度数为：

tgα=2/60=0.0333

α=1°.91”[17]

为什么这种计算结果会与第一种kamal代表的角度基本一致？从计算方法来看，因为后者取1指时，tg(α/2)=(1/60)，计算出的α/2需要乘以2才是实际纬度值，一个是tg(α/2)求出的角度乘以2，一个是tgα直接求角度，算出的数据结果较为接近。由前文可知，作为1°52′和1°36′的isba(指)都曾经在印度洋周边出现过，一指究竟代表的是1°52′还是1°36′，其差异是由于kamal的形制发生了变化，绳长从板长的5倍变成了6倍，才使一指对应的数值相应改变。

从以上情况来看，国内相关研究的结果与《关于阿拉伯人的航海仪器》中给出的数据看似相近，但操作原理却完全不同。由之前的计算过程可知，这里的72和60是几个数据相乘后的结果，不能直接简化成绳长或手臂的长度。而手臂的长度也因人而异，不宜作为固定数据引入计算，例如《中国古代的恒星观测》一文中就提到：“按作者自己手臂最远自然长度约为40厘米。”[22]

3 牵星板的计算功能与记录功能

《中国古代航海天文》中之所以采取垂直手持木板测星高的计算方法，实际是建立在中国南海社会调查的基础上，如书中记录1976～1981年间所做的传统天文导航方法调查：

(“掌度”)其法是：伸直右臂，手掌横向，指向左侧，张开手指，母指头朝下，与海面相切，尾指尖向上。若北辰星恰好在尾指尖上，这时北辰星的高度为1“掌”，1掌约相当于20厘米。若北辰星高1掌，表示船已到海南岛附近海面，若北辰星高半掌(北辰星在中指上)，表示船在越南南部以东海面。

……

(“尺量”)其法是：伸直手臂，竖直持尺，尺下端与海面相切，同时观测北辰星的寸数。詹细富收藏的《针路簿》手抄本中的“定子午高低法”中载；“吕宋子午高五寸六分，表尾子午高七寸二分，语屿门子午高一尺七寸。”[*]刘南威：《我国民间的航海天文》第36～37页。同书第103页“定子午高低法”这段原始记载的说明为“辑自惠安县崇武公社靖海渔业大队占伙木收藏的针路簿”。随后也有“辑自厦门市水运公司外海船队詹细富收藏的针路簿”一节，与这段文字大体相同。

在这些记录中值得*意的是，中国民间航海者用尺寸分的计量单位记录星高，而他们用更简单的“掌”测量北极星高度的方法，与本文第二节开头提到的19世纪30年代《关于阿拉伯人的航海仪器》开篇，阿拉伯海员并拢手指测北极星高的方法非常相似，只是阿拉伯海员测星的单位是“指”，而中国南海船员的单位则是“掌”[*]刘南威：《我国民间的航海天文》第36页中也提到：“这个指，应是手指的‘指’，其起源于向前伸直手臂，用手指量度天体的高度，这与沿海渔民的‘掌度’类同。”。可以推测，早期航海者测量北极星高度的方式很可能都是直接用手估算，如《中国度量衡史》中所述，古人最初设置度量衡标准时，常“以人体为则，如云‘布指知寸，布手知尺’”[24]。从相关信息中，可以推测古代印度洋上天体导航技术的发展历程：第一个阶段是原始的手指计数；第二个阶段开始使用简单的工具，用一系列以指为单位、每一块增加一指的木板代替手指计数；第三个阶段引入天文数学家的研究成果，将花剌子模杖中的木杆换成便携的绳子，改造成用若干绳结计量指数的kamal。用这种工具，甚至可以计算出观测者所在的地理纬度。

然而，使用kamal的普通航海者们真的都需要用这种工具计算纬度吗？虽然天文数学家们可以这样做，但古代印度洋上的航海者们未必都有相应的数学基础，而且要用kamal计算精确纬度，必须准确量出星高对应处的绳子长度，再配合三角函数表使用，但并没有记载显示每位领航员都必须在航海工具外再配备一本函数表。从古代航海文献来看，其中只有关于星辰高度的数据，而没有纬度记录，例如《印度洋航海记》中记载从阿拉伯南部海岸到印度古吉拉特的航程：

直到天箭座6指高或天琴座5指高……如果你朝向阿拉伯海岸，并且北极星在9指高左右，你可能靠近了印度的陆地。[*]Sidi Ali Celebi, translated by Joseph Von Hammer. Extracts from the Mohit, that is the Ocean, a Turkish work on navigation in the Indian seas, 1836.p.457. 原文是：“……till Sagitta is six inches or Lyra five inches……If you are leaning towards the Arabian shore, and the pole is made with nine inches or near it, it is guessed that you are come near the Indian land; ”原文中的“指”此时被译作inch，其实它就是阿拉伯航海中常用的isba。早期译者将其翻译作celestial inch, issaba inch，或直接简称为inch(Sidi Ali Celebi, translated by Joseph Von Hammer. Extracts from the Mohit, that is the Ocean, a Turkish work on navigation in the Indian seas, 1836.p.442～443; 1838,p.774)。关于古代阿拉伯导航技术，还可参考《葡萄牙人到来之前印度洋上的阿拉伯航海术》第三章《导航理论》：G.R.Tibbetts, Arab navigation in the Indian Ocean before the coming of the Portuguese, the Royal Asiatic Society of Great Britain and Ireland, 1971. pp.269～391.

在中国古代各种航海文献中也只有星高数据，例如前文所引《顺风相送》中的《古里往祖法儿》航线中描述：“过礁头开洋，辛戌五十更，看北辰六指三角，灯笼星八指三角；单辛七十更，看北斗七指三角，灯笼星七指三角，取祖法儿码头，水六托，泊船是也。”列出的都是各星的高度。又如《马可波罗行记》中记载：

戈马利是印度境内之一地，自苏门答腊至此，今不能见之北极星，可在是处微见之。如欲见之，应在海中前中前行至少三十哩，约可在一肘高度上见之。

马里八儿是一大国……在此国中，看见北极星更为清晰，可在水平面二肘上见之([15]，379～380，381页)。

虽然此处“肘”的具体含义尚不确定[*]如韩振华《我国古代航海用的量天尺》一文中即有分析，认为它是中国古代计量单位“寸”的音译。此处的“肘”在其他版本中也被译作“古密”(cubit)，其意义待另行撰文讨论。，但应当也是一种以高度代表角度的计量方式。从实际操作方法来看，牵星法的关键之处在于用标杆确定星辰在某一高度，然后航行时保证这个星辰始终在这个高度上，实际就是沿同一纬度前进。这种标杆可以是手臂、手指，也可以是直尺、木片，或是木板与绳结共同组成的工具。在没有现代计量工具和国际标准数据的年代，每个航海者只要保持星辰的高度在手掌或工具的某个位置，就可以实现同纬度航行，至于这高度究竟数值多少，对应哪个纬度，即使不知道也不会影响航行。而且相关工具和测出的数据也不需要达到国际统一标准，因为每个领航员只需要对自己的船负责，由于身高、臂长和指宽的差异，不同的人即使采用同一工具测量同一位置的同一星辰高度，也很可能测出不同的结果，但如果这些数据只由测量者本人使用，那么对于他和他所在的航船而言，这些数据就是可靠的，如果别的领航员需要使用这些数据，就要重新加以校正。如《印度洋航海记》中所说，每个领航员都要根据自己的手来使用木板，如果他个子较高，分割出的指就会大些，如果个子较低，各指之间的分隔就会小些；因此一定会存在差异，操作也不会特别精确([20]，771页)。

在1850年发表的一篇调查中，更显示了这类导航工具简单便利的特征。文章介绍了印度科罗曼德海岸的水手们使用的导航工具[25]，它的外形和上一节提到的kamal非常相似，也是由木片和绳子组成，木片长3英寸，宽1.5英寸，中心穿过一根18英寸的绳子，但绳子的打结方式却有所不同：航海者们如图8左侧所示，左手持木片，右手拉紧绳子，使木片的上缘和下缘分别对准北极星和海天连接线，当右手所牵的绳子碰到自己鼻子时，就在绳子与面部接触的位置打一个结。由于每个地方纬度不同，北极星的高度不同，所以绳子上打结的位置也不同，以后需要航行到相关地点时，只要按之前的操作方式，保持北极星的高度与相应绳结始终一致，即可航行到目的地。虽然文章称每个绳结如图8右侧所示，各自代表海岸线上一个著名地点的纬度，但航海者既不需要记住纬度的具体数值，也不需要做任何计算，绳结位置也与“指”这个计量单位无关。由于绳子只起到固定作用，它甚至不需要垂直于木板，这实际上是一种只有记录功能而没有计算功能的导航工具。

图8 左：海员使用简易工具测星高的方法右：每个绳结代表一个地名([25]，102页附图)

将中国海员与阿拉伯航海者的导航方式对比，可知中国海员以手掌测高，或用直尺以尺寸分单位记录星辰高度的方法，正与后者第一阶段的以手指测天，以及第二阶段用一系列木板测星高指数的状态对应。而后者第三阶段用kamal工具测算的方法，在中国则没有出现。明代的马怀德牵星板看起来与后者第二阶段的工具相似，但又有所发展，多出一块测角的象牙板和一到三指共3块小木板。由此看来，马怀德牵星板很像是介于第二、三阶段之间的形态，它有可能是一种未见于其他文献记载的分支技术，也可能是古代中国航海者根据中国传统测量天体的习惯，对印度洋上导航工具加以改造的结果。

马怀德牵星板中还有一块四角有缺口的象牙板，上面有“半指、半角、一角、三角”字样，看起来一指应是分为四角，即八个半角，而“半角”在阿拉伯航海书中的表达方式是zam。严敦杰文中认为：

阿拉伯人又用zam的单位，1指(isba)=8zam。则zam与上牵星板的半角相当。欧洲有些学者把郑和航海图中的指和角直译作isba和zam，其中角作zam是错误的([9]，78页)。

在古代阿拉伯航海书中，可以看到指和角的表达方式[*]如“十又二分之一指”(ten inches and a half)、“四又八分之一指”(four inches and an eighth)、“五又四分之一指”(five inches and a quarter)，“八指差四分之一”(a quarter less than eight inches)，其中“二分之一指”即半指，“八分之一指”对应的是半角，“四分之一指”即一角，“某指差四分之一”则是三角(Sidi Ali Celebi, translated by Joseph Von Hammer. Extracts from the Mohit, that is the Ocean, a Turkish work on navigation in the Indian seas, 1836: pp.463，468，464，465)。，换算成长度时，1指为0.75英寸，即1.91厘米([20]， 778页)。

李诩《戒庵老人漫笔》中称牵星板是“周髀算尺”，这可能是收藏者马怀德的解释，也可能是李诩根据自己理解的重新阐释。它应是指中国传统中偃矩望高、立杆测影的垂直测量方法，与中国海员手持直尺测天的方式相同。从计算思路来看，用三角函数和天文数学工具测算纬度，其前提应是认识到地球为一球状体，考虑到中国古代的三角学发展和对地球的认识情况，相应知识要在明朝后期传入国内之后才被国人普遍接受，因此，即使明代中前期的航海者们在海外接触到kamal和纬度计算方法，恐怕也不能理解并认同其原理[*]陈忠烈《相会在星空——十五至十七世纪东西方的航海天文》从科学传统的角度出发，分析了东西方航海天文的差异，可为这一问题提供参考。。在这种情况下，中国海员们完全可以像印度洋上很多普通的航海者一样，仅通过记录星高的方式航行，而不必了解具体纬度及其计算方法。可以想见，当中国海员航行到印度洋时，当地航海者都用指角作为计量单位说明和记录航海路线，为便于交流，中国海员也需要入乡随俗，以当地海员的测量工具和计量单位记录星高，而不必将它们再换算成尺寸分。

马怀德牵星板与阿拉伯航海文献中记载的一系列木板不同之处，除了不确定究竟有没有绳子，还多出了一块“四角皆缺”的象牙板，其长度在古籍中有“长二尺”和“长二寸”的不同记载。既然是用来计量半角到半指的小刻度，这块象牙板也只可能是二寸长，严敦杰文中认为它是四角斜割，而金秋鹏文中认为它是四角方形缺口，这样它的形状看起来会像一个不规则的十字架。从实际情况考虑，这两种形态都有可能存在，但方形缺口更便于使用，因为可以用来与乌木板叠加。同样，马怀德牵星板中不管是否存在绳子，也都不会影响测量，因为它不参与计算，只能起到固定和收纳作用。事实上，如果这套牵星板能在操作台上搭配水平木杆和垂直木槽使用，效果会比绳子更好，因为这种观测会受到测量者身高、臂长的影响，且绳子多次使用后未必还能保持原有性能，而操作台可以确定观测高度，木杆可保证观测距离不变，木槽也可以更有效地固定乌木板与象牙板。

在现存的中国古代航海文献中，有些星辰高度达十四指、十五指，测量范围已超出马怀德牵星板最高的十二指。如《郑和航海图》中记载：“时月正回南巫里洋，牵华盖星八指，北辰星一指，灯笼骨星十四指半，南门双星十五指……”[26]这种现象的原因可能是这片海域与马怀德牵星板的测量范围并不完全匹配，即这套牵星板的使用者不需要航行到星高超过十二指的海域，也有可能是马怀德牵星板原本还有从十三指到十六指的四片木板。还有一种可能是，乌木板之间可以叠加使用，当星高超出十二指时，可以将一指、二指、三指的小木板逐次叠加到大木板上尝试，直至测量出实际高度为止。马怀德牵星板与《印度洋航海记》中记录的类似工具比较，其中多出的一指到三指共3块小木板，其用途之一或许正在于此。

4 明代之前中国航海中的天文导航

从现有文献来看，中国古代航海中所用的天文导航方法仍是简单测高，此前研究中曾提到几例在明代之前以计算方式进行天文导航的证据，除了开头提到的泉州南宋沉船上的竹尺和马怀德的身份之外，《中国科学技术史》中还提到了三条证据，第一条的内容是：

我们能找到关于中国勘测人员采用“指宽”(“指”)作为量度单位的记载，其时间比阿拉伯文化中任何类似的量度记载都要早……(“邓艾每见高山大泽，辄规谋度指，画军营处所，时人皆笑之”)……当然，以指宽为单位测量高度的方法，也极有可能分别独立地出现于阿拉伯和中华文化圈。[*]这段原文是：Moreover, we can find possible Chinese mentions of surveyors’ measurements in ‘finger-breadths’(chih) a good deal earlier than anything similar in Arabic culture. For example, as has already been noted, one of the Wei generals, Teng Ai, was well known about +260 for his interest in military topography——’whenever he saw a high mountain or a wide moor, he always estimated(heights and distances), measuring by finger-breadths, so as to sketch and plan the best positions for an army camp or fort’. His contemporaries, easily amused, thought this rather pedantic. But of course the system of finger-breadth units for altitudes could easily have arisen independently in the Arabic and Chinese culture-areas.(Joseph Needham: Science and Civilisation in China, Volume.4: Physics and Physical Technology, Part III: Civil Engineering and Nautics. Cambridge University Press. 1971. p.573.) 此处获科学史所邹大海研究员提醒，关于邓艾的这条记载发生在其早年为小吏之时，尚未上战场，而《中国科学技术史》中误将这条记载置于邓艾晚年为将之时，其间年代相距甚远。现在此补充说明，特致感谢。([12]，623页)

这段文字中邓艾的事迹源于《三国志·邓艾传》。《中国科学技术史》英文原版中没有引《邓艾传》的汉语原文，但据其叙述可以推测作者解读原文时在“指”、“画”之间断开，将“度指”视为一个词；汉译本附有汉语原文，且较《三国志》通行本在“规”、“度”之间多出一个“谋”字。而中华书局标点本对这段的断句是：“(邓)艾初不称谢。每见高山大泽，辄规度指画军营处所，时人多笑焉。”[27]在古代文献中，“规度”和“指画”是两个不同的词[28- 29]，这里原本不应有“度指”一词，实际应是“规度”、“指画”。这只是断句引起的误会，不能认为邓艾使用了指宽作为量度单位。

第二条是《中国科学技术史》中认为中国的弩机与kamal等导航工具相似，由此推测15世纪的中国领航员使用十字仪([12]，624页)，所引原文如下：

从沈括所说的一段值得*意的话可以看出，中国人早在十一世纪(即在宋代)就已经知道十字仪，而使用十字线网格则可以上溯到汉代。下面就是沈括的这段话：

有一次，当我在海州的一所房屋的花园里挖土时，曾挖掘出一个弩机。当你用它来观测山的整个宽度时，弩机上的距离很长……[30]

虽然弩机与kamal等工具在外形上有相似之处，但从本文第2节的考证中可知，kamal的核心原理是计算圆心角，而弩机的原理则是相似三角形，两者使用的方式和依据的技术原理不一样，不能认为它们是同一种工具。

第三条是宋代海船上的“望斗”，《中国科学技术史》中对原文解读如下：

〈(建炎三年)三月十二日……船合用望斗、箭隔、铁撞、硬弹、石炮、火炮、火箭及兵器等，兼防火家事之类。〉

虽然我们在别处还未曾遇到过“望斗”这个名称，但它的意思显然是指用来观测大熊座位置和高度的窥管……“望斗”也同样可能是一种十字仪或阿拉伯牵星板。所以，对于中国领航员来说星体高度的测定也许是紧随天体方位的测定而发展起来的。([12]，625～626页)

但从一些军事史料中可以看到，望斗是中国古代战船上的一种战斗装备，如图9所示，是安装在桅杆顶部，外形如斗的厢体，可以用于瞭望，也可以向外放箭，这里的士兵被称为“望斗兵”，与天文观测并无关系。如《兵录》中记载：

桅顶用望斗，以布作围，藏兵在上，以了贼舟。([31]，620页)

图9 明代战船桅杆顶处的望斗和望斗兵([31]，622页)

从以上史料分析来看，邓艾的“度指”、宋代的弩机和望斗几例证据都不成立，所以不能认为中国古代曾经出现过独立的天文导航工具。然而没有独立工具不等于没有天文导航方法，《牵星术》一文中提到：“唐代南宫说在开元十二年(724年)的疆土测量中，已准确定出北极高度与南北里程的关系，此后不久即有可能将这一原理用于海上。”[33]近年有《海中识方位——航海南北定位在中国古代开始应用时间探析》一文提到早期中国文献中常以为日本在海南岛附近，直到唐代后期，文献中才能准确认识日本在北方的位置，也为此提供了一条旁证[34]。

中国古代航海文献中的牵星数据之所以只出现在印度洋及其周边，是因为相关海域中常不见陆地标识，所以只能依据天文导航。而在中国附近海域，由于陆地标示较多，海中常有山石相望，所以未将牵星术作为主要导航方法。从人类航海史发展的角度来看，应用在海上的技术通常是由内陆技术演化而来，中国内地堪舆术中常使用罗盘勘测，所以海船上较早使用指南针，而阿拉伯航海者惯用的星高导航方式，也能在陆地上找到它的原型。《古代阿拉伯航海技术》中分析阿拉伯人在内陆同样需要用星辰引路[35]，如《古兰经》中记载：“他为你们创造诸星，以便你们在陆地和海洋的重重黑暗里借诸星而遵循正道。”[36]这反映了当地人的早期生活状态，之所以在陆地上也要凭借星辰识途，是因为当地多沙漠，人们在其中穿行时，茫茫沙海常与海洋一样漫无标志，所以旅行者们只能依靠星辰定向。由于生活环境和历史传统的影响，当地航海者将牵星法的使用范围从陆地扩展到海洋。

中国古代早期与天文记录有关的“指”用来表示人们估测天体的距离[*]关于中国古代天文文献中的“指”，详见王玉民：《以尺量天:中国古代目视尺度天象记录的量化与归算》第三章第五节《“指”系统、牵星术及其他》，第64～65页。，它很可能也是当时人们用身体部位作为度量衡的表现，与明代海道针经中印度洋周边的天文导航计量单位“指”的本义有一定相似之处。从印度洋上的导航工具来看，明代航海书中的“指”应当就是isba的意译，在明初之前，可能已经有许多中国民间航海者接触到这种计量单位，但它的正式引进、普遍使用和流传，应当是在郑和下西洋时期。当古代中国海员与印度洋上的航海者交流导航工具和方法时，很可能与后来的欧洲观察者们一样，看到了当地海员用手指测星高以解释计量单位的情形。这种解释是中国海员们可以理解的，因为它与中国传统的掌度和直尺测天方法基本相同，而中国内陆的量天尺正是以尺寸分为计量单位[37]。所以再回到本文开头，虽然泉州湾海船中出土的尺子不具备特殊形制，但它依然有可能是导航工具，因为中国传统航海活动中的天文导航工具原本就是普通的尺子。

5 总结

从天文导航技术的发展过程中，可以看到世界各地的航海者们都有用手简单估算星高的传统，除了中国南海船员的“掌”、印度洋边海员的“指”之外，太平洋上南岛语族的土著航海者们也用手指和手掌估测星体出水高度以导航定位[38- 39]，这应当是世界各地先民们普遍的生活状态。由于科学技术传统和地理环境的差异，中国与印度洋周边的导航技术向不同的侧重方向发展，在现存的航海指南中，可以看到前者更多描述更路和岛礁等陆标辨识，而后者更多描述星辰、风浪和生物。当中国古代航海者来到印度洋海域时，为便于交流，以入乡随俗的方式借鉴了当地常用的测星工具和计量单位，但仍然是以中国传统方式使用，正体现了两种导航传统在这一时段的不同趋向。

在印度洋上航行时，虽然用kamal这样的牵星工具可以粗略算出船舶所在的纬度，但这并不说明所有的牵星工具都有计算功能，也不能说明所有的航海者都必须在量出星高之后还要继续计算纬度。事实上，一些论著中也已*意到这种现象，如《略论牵星板》开头即阐明“牵星板是过洋牵星时用于测量方位星出地高度的观测仪器。过洋牵星术是一种天文航海术，它通过对于方位星出地高度的测量，进而测定船舶在大海中航行时的航向和方位，是古代远洋航行中重要的测向定位技术”([11]，83页)。但自从《牵星术——我国明代航海天文知识一瞥》做出“用牵星板以测定船舶所在的地理纬度，实为我国航海天文仪器的先声”([9]，88页)这一结论后，很多论著中没有强调记录功能与计算功能的区别，以致许多读者认为所有古代航海者使用牵星法时，都必须计算出具体纬度，这实为一种误解。