一种基于PSFS的近红外人脸3D形貌重构系统

王国珲，吴二星，王立平

(西安工业大学 光电工程学院，陕西 西安 710021)

近年来，利用人脸识别的身份认证技术(又称“刷脸认证”)已成为门禁系统、账号登录、支付验证等常用的身份认证手段。然而，当前的人脸识别技术几乎都是基于人脸的2D图像，若光照度及人脸姿态、表情变化较大时，识别准确率较低；另外，还可能受到假人脸的欺骗，如用人脸照片冒充活体人脸，造成安全性下降。因此，融合人脸3D形貌的识别技术是未来人脸识别发展的趋势，它能够有效地避免光照度、人脸姿态、假人脸等因素的影响，从而可以提高安全性和识别率。

对于人脸3D形貌信息的获取一般有主动式和被动式两种手段。主动式方法是使用特殊的光源装置提供目标人脸的照明，由相应探测器接收到人脸表面反射的光线的信息，利用几何关系计算出人脸表面的3D形貌。典型的有飞行时间法和结构光法：飞行时间法采集速度较快，但是形貌信息精度较低、分辨率不高；结构光法虽可以获取较高的精度和分辨率，但测量时间较长，还可能造成对被采集者的干扰或侵犯。被动式方法不需要特殊的光源装置，直接由自然光或普通光源对目标人脸进行照明，从一个或多个相机获取的2D图像中提取3D形貌信息。代表性的有立体视觉法和Shape from X方法。立体视觉法测量精度较高，对环境无特殊要求，但需要对每台相机进行标定，标定过程繁琐，且图像中特征点匹配算法也较为复杂。Shape from X方法基本上是利用图像的灰度信息来获取目标的形貌信息。其中，从明暗恢复形状(Shape from Shading，SFS)是一种典型的被动非侵犯式3D形貌获取手段[1]，它能够快速、有效地提取目标表面的几何形貌信息，其分辨率高、适用性强，广泛应用于工农业产品检测[2]、医学图像分析与重构[3]、扫描电镜图像3D重构[4]、月面与火星表面形貌测量[5]以及人脸3D形貌重构[1,6]等领域。

文献[1]与文献[6]等基于SFS的人脸3D形貌重构系统中，在建立人脸表面的偏微分辐照度方程时，通常采用朗伯光照明模型来描述人脸皮肤的光学属性。然而文献[7-9]证实了对于实际的人脸皮肤，不论是在可见光照明还是在近红外光源照明下，使用朗伯光照明模型来描述其光学属性是不精确的，而使用Oren-Nayar光照明模型[10]可以取得较好的效果。基于上述结论，本文设计了一种基于Oren-Nayar光照明模型的人脸3D形貌重构系统。根据文献[7-9]的建议，系统采用了近红外光源照明，这是因为在近红外光源下人脸皮肤对入射能量(辐照度)的反射特性(辐射亮度)更适合Oren-Nayar光照明模型；同时，近红外光源照明还可以避免对被采集者的干扰或侵犯。此外，相机的成像过程接近透视几何变换，因此系统采用了基于透视变换的SFS(Perspective SFS，PSFS)方法。

1 近红外人脸3D形貌重构系统

如图1所示的基于PSFS的近红外人脸3D形貌重构系统，由被采集的人脸表面、近红外光源、相机(含镜头和近红外滤光片)以及上位计算机等部分构成。

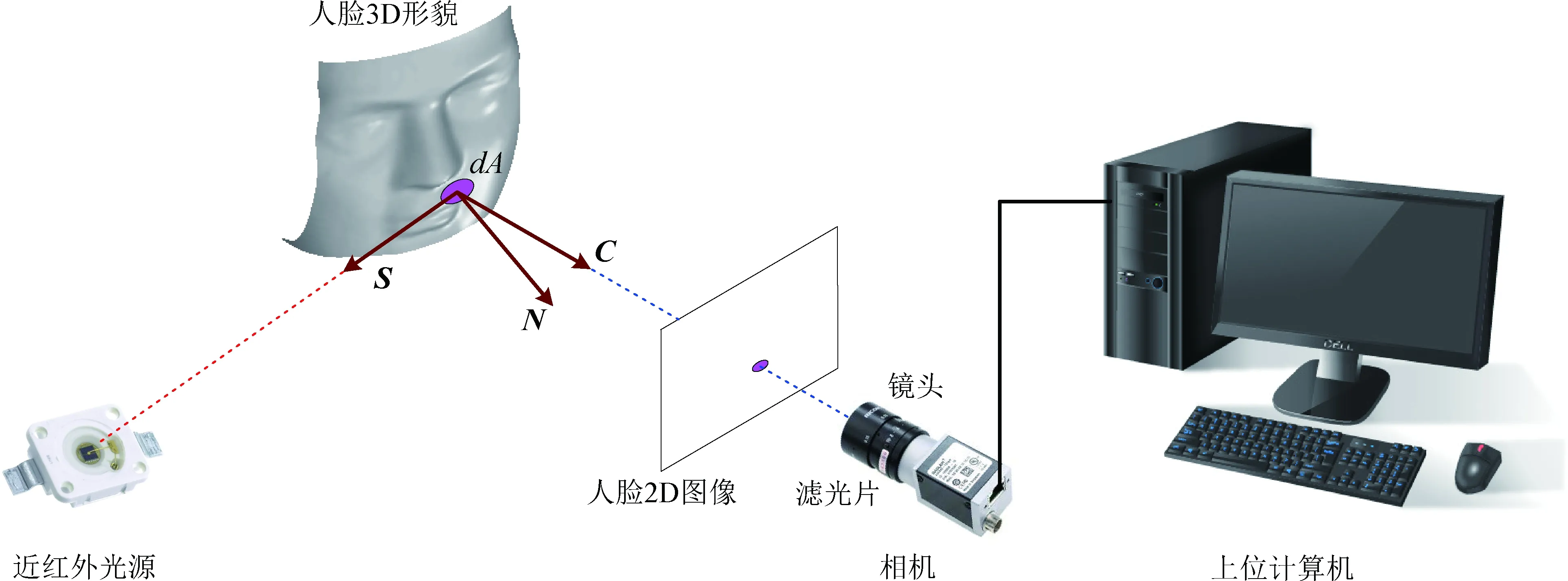
图1 基于PSFS的近红外人脸3D形貌重构系统示意图

系统中，近红外光源采用Osram公司的LED光源，型号为SFH 4235，其中心波长约为850 nm，半强度宽度约为30 nm。由于LED光源发光面尺寸较小，远小于光源到人脸表面的距离，因此可认为LED光源为点光源，此时近红外点光源(辐射强度为I0)发出的辐射能量在人脸3D形貌微面元dA上形成的辐照度近似正比于N·S，式中N为人脸3D形貌微面元dA的法向量，S为微面元dA到点光源的方向向量。

人脸皮肤接收到LED光源的辐射能量(辐照度)，对其进行反射(辐射亮度)，反射的能量被镜头会聚后进入相机。为了节省系统成本，系统中没有直接采用近红外相机，而是基于“普通相机+近红外滤光片”的模式，采用Basler公司的ace相机，型号为acA640-100gm，其光谱响应曲线如图2所示。

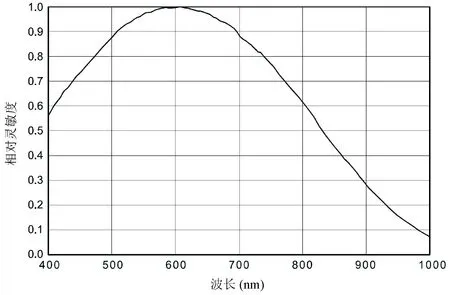
图2 acA640-100gm相机的光谱响应曲线

由图2可见，该相机在LED光源中心波长850 nm处的相对光谱灵敏度约为45%，因此配合810nm的近红外滤光片可以取得较好的近红外成像效果。相机获取到的2D图像信息(图像灰度)与成像时人脸表面3D形貌造成的反射光强弱密切相关。图像灰度信息由相机的数据输出接口——网口送入上位计算机。上位机系统软件求解图像灰度信息与人脸3D形貌相对应的偏微分辐照度方程，最终可以获得人脸的3D形貌。

2 近红外人脸3D形貌重构系统软件设计

本文的工作重心为近红外人脸3D形貌重构系统软件的设计与实现，其核心任务就是求解图像灰度信息与人脸3D形貌相对应的偏微分辐照度方程，涉及的内容包括：系统坐标系的建立、近红外成像条件下人脸皮肤光学属性的描述、人脸表面偏微分辐照度方程的构建、偏微分辐照度方程求解算法的设计与实现。

2.1 近红外人脸表面偏微分辐照度方程

2.1.1 近红外人脸3D形貌重构系统坐标系

以相机(镜头)的透视中心建立如图3所示的3D笛卡尔坐标系o-xyz：透视中心o为重构系统坐标系的原点，镜头的光轴为z轴，坐标系的x轴、y轴分别与相机成像平面中u轴、v轴平行；相机的成像平面u-v位于z=-f处，f>0为镜头的焦距。

图3 近红外人脸3D形貌重构系统坐标系

由于相机的成像过程接近透视几何变换，在上述坐标系下，人脸3D形貌某一点(x,y,z(x,y))在成像平面u-v上的几何投影为(u,v)，投影光线方向向量记为C，并有

(1)

(2)

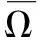
2.1.2 近红外成像条件下人脸皮肤光学属性

根据文献[7-9]的研究成果：对于实际的人脸皮肤，不论是在可见光照明还是在近红外光源照明下，使用朗伯光照明模型来描述其光学属性是不精确的，而使用Oren-Nayar光照明模型[10]可以取得较好的效果；尤其是在近红外光源照明下，人脸皮肤对入射能量的反射特性(辐射亮度)更适合Oren-Nayar光照明模型。基于Oren-Nayar光照明模型，人脸3D形貌微面元dA的辐射亮度为

(3)

式中：ρ为人脸皮肤的反射率，本文中假定ρ为恒定值；A=1-0.5σ2/(σ2+0.33)，B=0.45σ2/(σ2+0.09)，σ代表了人脸皮肤的粗糙度；α=max[θi,θr]，β=min[θi,θr]，θi,φi和θr,φr分别为入射光线方向向量S、投影光线方向向量C相对于人脸3D形貌微面元dA的法向量N的天顶角和方位角。

重构系统在设计时，使得近红外点光源位于相机的透视中心o附近，此时近似有

α=β=θi=θr;φr=φi

(4)

在上述条件下，人脸3D形貌微面元dA的辐射亮度为

(5)

2.1.3 人脸表面偏微分辐照度方程

由相机采集到的图像信息与近红外点光源辐射强度、人脸表面的辐射亮度之间的关系[5,11]可得到

I(u,v)=Acosθi+Bsin2θi

(6)

式中：I(u,v)为相机获取的图像灰度，它的明暗变化与成像时人脸表面3D形貌造成的反射光强弱密切相关。

由人脸3D形貌微面元dA到近红外点光源的入射光线的单位方向向量S为

(7)

利用微分几何可求得微面元dA的法向量N为

(8)

由于θi为S与N之间的夹角，由式(7)和(8)可得

(9)

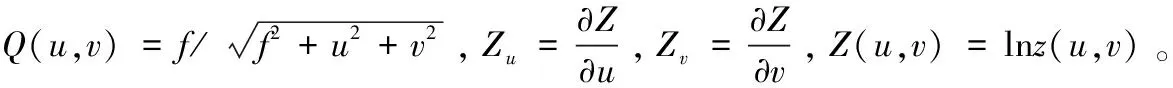
(10)

其中：R(u,v)=

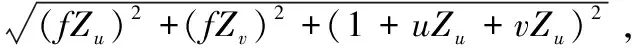
2.2 偏微分辐照度方程求解数值算法

对于人脸表面偏微分辐照度方程(10)，可视为R(u,v)的方程：

[I(u,v)-B]R2(u,v)-AQ(u,v)R(u,v)+BQ2(u,v)=0

(11)

显然，式(11)是关于R(u,v)的一元二次方程。求解方程(11)，且满足R(u,v)≥0，可得

(12)

又由于R(u,v)=

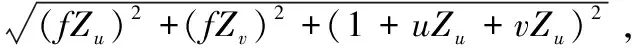
(13)

显然，方程(13)是一个H-J类的偏微分方程，可应用本文作者在文献[12]中提出的求解数值算法逼近上述H-J类方程的解，其详细过程如图4所示。

图4 偏微分辐照度方程求解数值算法逼近过程

3 实验

分别通过系统合成的(已知3D形貌)和实际拍摄的人脸2D图像进行实验，验证近红外人脸3D形貌重构系统的有效性，结果如图5、图6和图7所示。

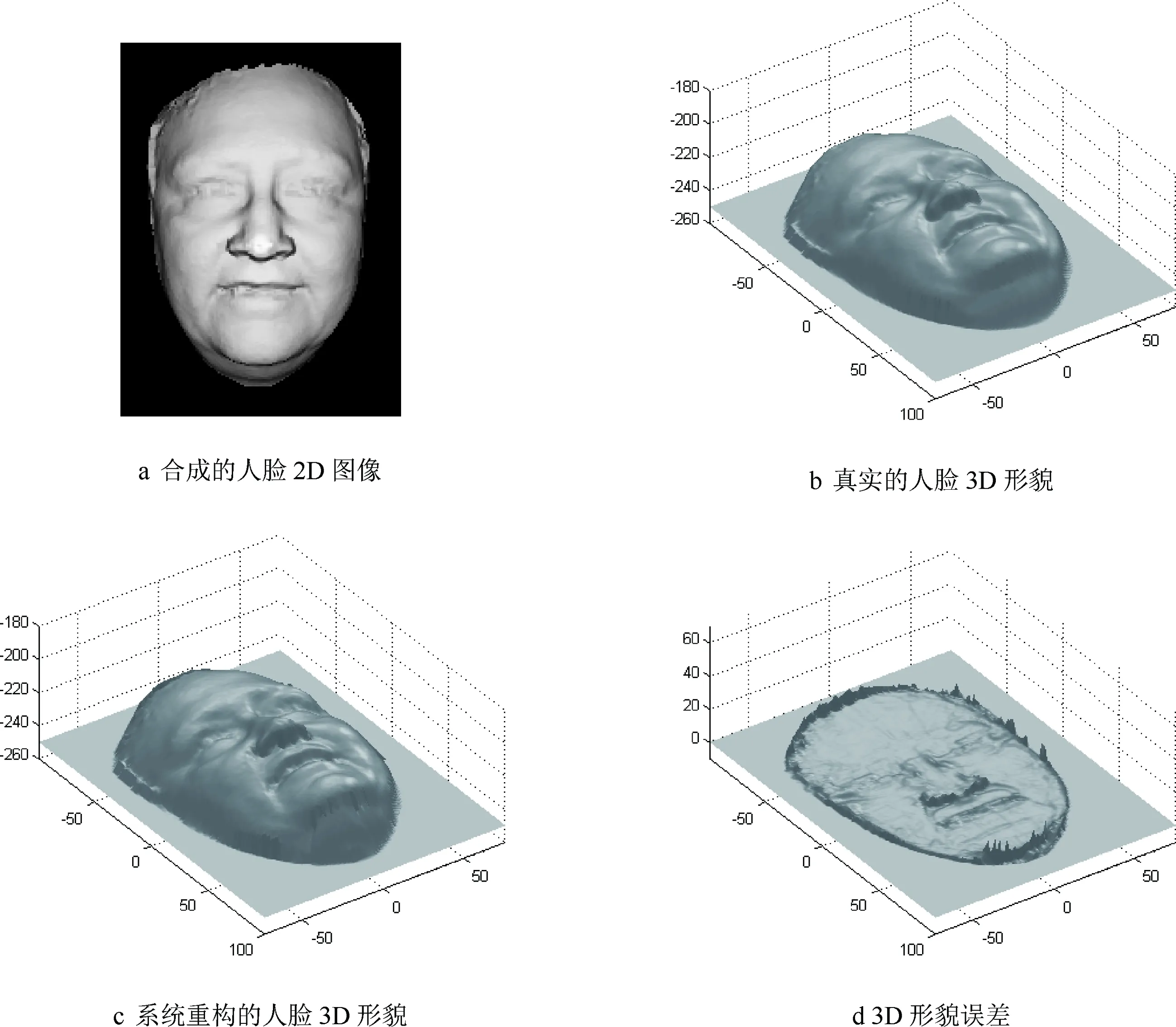
图5 已知3D形貌的人脸重构结果

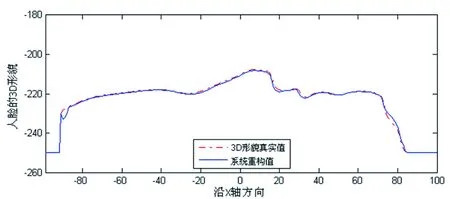
图6 人脸3D形貌的中心横截面

图7 实际拍摄的人脸重构结果

图5a是一幅已知3D形貌的人脸2D图像，由系统通过算法合成得到，图像的灰度级为256级，图像的分辨率为200×150；图5b是图5a对应的真实3D形貌，单位为像素；图5c为使用本系统重构的人脸3D形貌；图5d是图5b与图5c之间的3D形貌误差图。为了定量地评定重构结果，使用平均绝对误差(mean absolute error，MAE)(14)和均方根误差(root mean square error，RMSE)(15)对重构结果进行了评价。

(14)

(15)

图6是人脸3D形貌真实值(图5b)、本系统重构值(图5c)的中心横截面的比较结果，从图6中可以看出本系统重构的人脸3D形貌非常接近真实的人脸3D形貌，大部分区域真实值与系统重构值基本上保持一致，误差较大的区域主要集中在边缘部位，这也是本系统算法的限制所在。

图7a是本系统拍摄的人脸2D图像，图像的分辨率为494×659；图7b为使用本系统重构的人脸3D形貌。由图7a可以看出，在近红外光源照明下，图像的明暗变化较为平滑，因此更适合Oren-Nayar光照明模型。由图7b可以看出，本系统重构的3D形貌甚为逼真，3D形貌的变化趋势与2D图像明暗的变化基本保持一致；在额头、下巴及鼻子、腮部等处效果较好，而在眉毛、眼睛处效果稍差，这是因为眉毛、眼睛处的反射率与皮肤的反射率不一致，而本系统假定整个人脸反射率恒定所造成的。

综上，由图5、图6和图7所示的人脸3D形貌重构结果以及计算得到的MAE、RMSE值可以看出，本重构系统能够获得较高的重构精度。

4 小结

本文设计了一种基于PSFS的近红外人脸3D形貌重构系统。在分析了人脸皮肤在近红外成像条件下光学属性的基础上，利用Oren-Nayar光照明模型结合以相机透视中心为原点建立的重构系统的坐标系，构建了人脸2D图像明暗变化与3D形貌相对应的偏微分辐照度方程，该方程实质上是人脸3D形貌梯度函数的二次方程，求解此方程可以得到H-J类的偏微分方程，利用求解数值算法逼近H-J类方程的解，最终获得人脸的3D形貌。系统合成的和实际拍摄的人脸2D图像实验结果表明，该系统能够有效地实现人脸3D形貌重构，并可获得较高的重构精度。