基于低秩矩阵分解的遥感图像薄云去除方法

古 今， 何 苗， 王保云

（1. 上海理工大学 上海-汉堡国际工程学院，上海 200093；2. 云南师范大学 信息学院，昆明 650500）

遥感卫星获取数据时，由于云层的覆盖，传感器较难捕捉到地面的清晰图像信息，给卫星获取该地区的有效图像造成了困难。同时，大范围的云层遮盖对图像清晰度和可辨识度产生了较大影响[1]，给图像处理造成障碍。同时不利于后期的图像应用，如对地观测、环境污染监测、军事目标识别及航拍定位等。因此，如何有效地去除云的影响仍是遥感图像处理中十分重要的问题。

当云层较厚时，被遮挡区域的地表信息很难透过云层被传感器接受，在没有借助任何辅助信息的情况下，要还原地表信息难度较大；而在云层较薄的情况下，一部分地表的图像未被全部遮盖，可以透过云层被传感器捕捉和感知，因此，在这种情况下，去除薄云，还原该地区的地表图像是可能的。

就目前而言，多光谱遥感图像去云法、图像融合去云法、同态滤波去云法、小波变换去云法是常见的遥感图像去云方法。其中，小波变换去云法和同态滤波去云法较为成熟。早在1996年，赵忠明等[2]提出了基于同态滤波的遥感图像薄云去除方法，对大面积的薄云去除取得了较好的效果。随后，很多学者，如冯春等[3]、刘健等[4]在同态滤波的基础上进行了改进，薄云去除效果取得了更进一步的提升。同态滤波法计算简单，能够保留感兴趣区域的细节信息，但是，容易在有云和无云区域的边界处产生边界效应。为了克服同态滤波方法的缺陷，引入了小波变换去云法[5-6]，该方法能够较好地保留细节信息和避免边界效应。但是，小波变换在对信号进行平移变换时，会导致小波系数的能量在各尺度上分布不均，并且限制了小波变换的方向。小波变换和同态滤波去云的方法主要是针对单幅或单波段图像，容易造成信息丢失。为此，多光谱遥感图像去云法[7-9]和图像融合去云法[10-11]得到了发展。多光谱的去云法是基于可见光和近红外波段对薄云的敏锐感知，该方法将云层信息单独提取出来，从原始图像中减去云层信息，从而去除薄云影响。该方法虽然能够克服单波段图像去云处理中信息丢失的缺陷，也较好地避免了去云过程中产生的其他副作用。但是，它需借助冗余波段作为辅助信息进行薄云去除，对传感器以及应用场景的要求较高。图像融合去云法主要是利用不同传感器在不同时间获取的数据，对有云区域的影像进行配准和替换。该方法对信息的有效融合能够较好地去除云层的影响，但对图像校正和配准有较高要求，在配准、校正和替换中容易影响图像的空间分辨率和光谱特征。除此之外，遥感图像薄云去除方法还有暗元法[12]、缨帽变换法[13]、机器学习方法[14]等。这些方法在遥感图像薄云去除时均存在去除不彻底或损失细节信息等缺点。

基于上述分析，目前针对薄云的处理方法仍有着各种不足之处。压缩感知在信号处理、图像处理及机器视觉等各领域得到了较为广泛的应用。在压缩感知理论的影响下，稀疏表示成为图像处理的有效工具。因此，本文将低秩矩阵分解应用在遥感图像的薄云处理中。低秩矩阵分解作为一种重要的数据采集和表示方式，能够有效地从具有噪声的图像中恢复出低秩的自然图像。根据地学信息的地理时空相关性以及云雾成像原理可知，在很多情况下，遥感图像结构的相关性很强，大部分区域的图像纹理也存在较大的相似性[15]，尤其是大面积薄云的分布较均匀，纹理结构趋于同一，整个遥感图像的矩阵呈现出低秩的特性。以上特征为矩阵低秩分解应用于遥感图像处理提供了理论支持。基于此，本文提出了一种利用低秩矩阵分解的遥感图像薄云处理算法。首先对图像信息进行低秩矩阵分解，将图像分割为前景、背景和薄云图像。然后去除薄云，融合背景与前景，得到地物成分，以此来解决现有方法中存在的缺陷。通过实验验证，本文方法能够较好地去除薄云。

1 薄云干扰下的数据模型

1.1 成像模型

由遥感图像成像原理可知，图像的辐射信息可分成两部分：一为空间传感器直接接收到的地物图像，属于目标对象；另一为在成像、传输等过程中外部叠加的干扰，属于去除对象。如式（1）所示。

式中：Y为获取的整体遥感图像；X为目标地物图像信息；N为干扰噪声信号。

在云雾天气出现时，薄云遮挡作为一种不可避免的噪声信号，对遥感图像产生了相当明显的影响。因此，受到薄云干扰后的图像模型，由式（1）变为式（2）。

式中：Y为接收到的受薄云污染的原始遥感图像，由三部分组成；X为希望获取的地物图像；C为薄云；N为其他噪声，如图像在拍摄、传送、处理过程中产生的噪声。得益于传感器和信号传输技术的发展，系统和随机噪声对图像质量的影响已较小。相比之下，薄云遮挡对成像质量的危害更为明显。薄云不仅会影响图像的可识别度，也对后续的图像处理和应用造成了障碍。因此，为了获取清晰可用的图像，重点在于如何从图像中，最大可能地消除薄云的成分。

1.2 数据模型

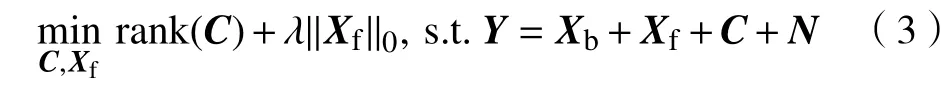
因为，式（3）的求解为NP-hard问题，较难直接求解。因此，将rank函数松弛为核函数，将函数松弛为范数[16-17]，可将式（3）写为式（4）的形式。

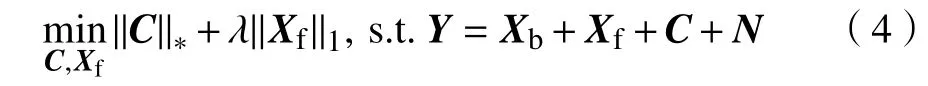
式（4）中的目标函数并不是一个可微的凸函数，但与式（3）相比，其可解性已经有了很大的提升。

2 模型求解

2.1 矩阵分解理论

根据模型求解的需要，引入两种优化算子对矩阵进行优化，从而求解模型[18]。

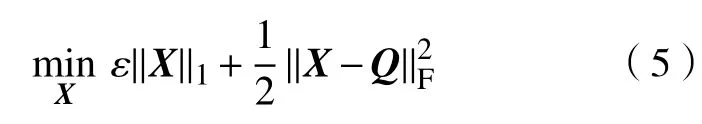
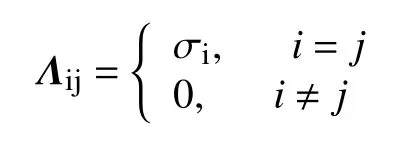
2.2 模型求解方法及过程

国内外学者针对式（4）的数据模型给出了多种求解算法。如Beck等提出的迭代阈值法[17]、Ganesh等提出的加速近端梯度法[18]及Lin等提出的增广拉格朗日乘子法[19]等。本文采用的方法为增广拉格朗日乘子法，增广拉格朗日函数构造如下：

针对此类问题，一般常用交替迭代法来求解。式中参数μ为式（4）中信号表示误差二次项的惩罚因子，可采用更新算法

W为表示误差一次项系数，迭代较为容易，可采用梯度下降法。更新算法为

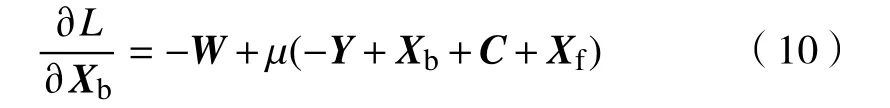
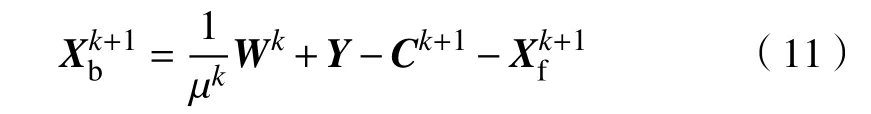
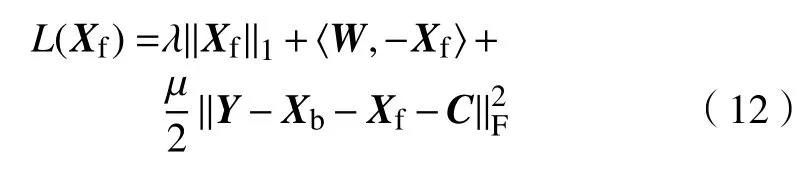
然后对式（12）等式两边进行配方，消去常数项，可得

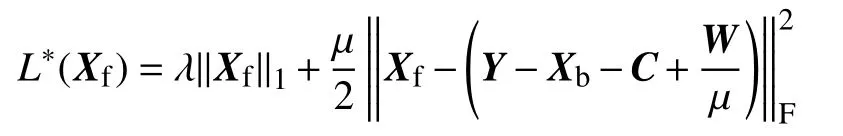
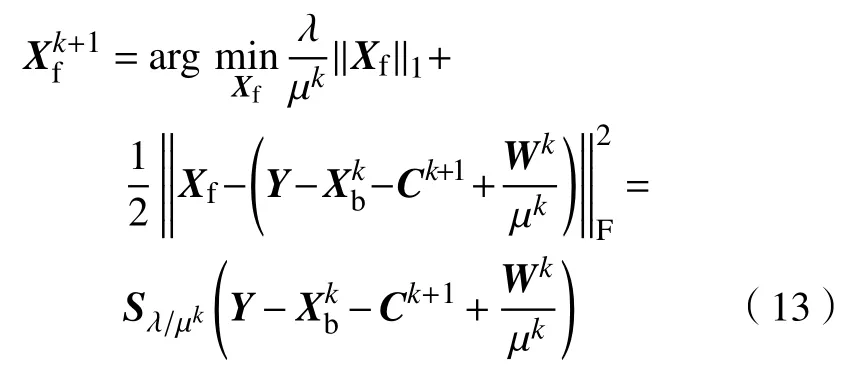
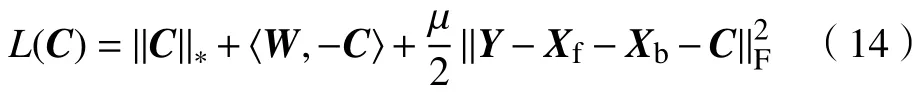
然后对式（14）配方，消去常数项，可得

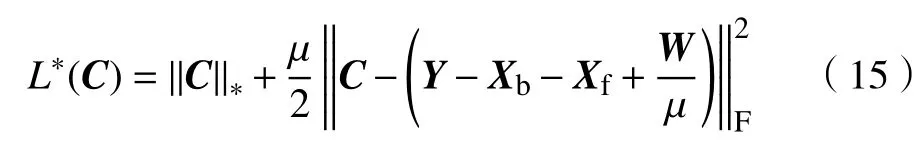
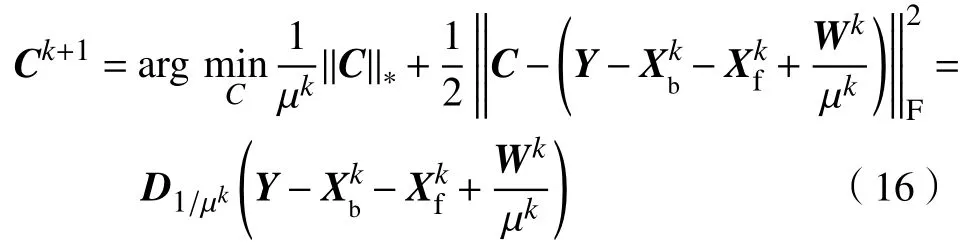
3 算法流程及实现

3.1 算法流程

现介绍算法的具体实现。算法1为算法的伪码，给出了具体步骤的描述。图1为算法的流程图。

算法1。

c. 重复。

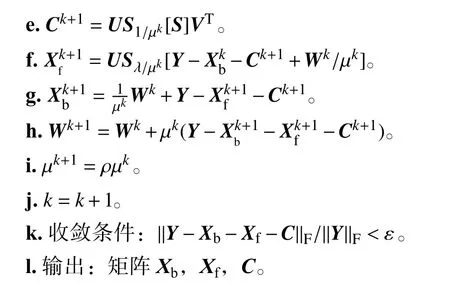
图 1 算法流程图Fig.1 Algorithm flow diagram

3.2 算法实现

对遥感图像薄云的去除可以分为5步：

a. 图像灰度转换。将原始的彩色遥感图像转为灰度图。

b. 图像分割。对转换后的灰度图等尺寸分割，分割尺寸为40×40。

d. 图像矩阵融合。根据c，低秩矩阵分解的结果，从原图信息中减去薄云信息。接着对前景信息矩阵与背景信息矩阵进行融合，即可得到去除薄云干扰后的图像。

e. 平滑处理。所有图像块都处理完之后对其进行平滑处理，得到最终的去云后的图像。

算法采用Matlab软件进行编程，其中，核心的步骤为低秩矩阵分解中的核函数和范数的求解。根据已有研究结果，采用文献[18]中的奇异值收缩算子和软阈值收缩算子对核函数和范数进行求解。

4 实 验

所有实验均采用Matlab（2014a）软件编程实现，实验数据选自2016-07-18北京市的一幅分辨率为16 m的高分一号卫星影像数据，选取源影像4个波段中的3个可见光波段合成彩色图像，经裁剪处理后图像大小为25 600×25 600像素。因实验处理对于图像尺寸的要求，需要对源图像进行预处理。首先对图像进行分割，等尺寸分割为200张各128×128像素的图像。随后根据上述算法流程，对每一张图像进行相应处理。

为了验证薄云去除方法的有效性，使用200张灰度图像进行了仿真。为了方便比较，选取了4张代表性的图像进行处理和分析，并采用其他3种传统算法与本文方法进行对比。4张图像为4种典型的地貌，分别为森林区域、山脊区域、道路区域和岩石区域。使用的其他3种算法为同态滤波、暗元法以及小波变换法。同时，使用3种计算参数作为主客观指标，分别为峰值信噪比[6,20]、结构相似度[6,20-22]及信息熵[6,20]。

4.1 评价指标计算公式

a. 峰值信噪比PSNR。峰值信躁比是最广泛使用的图像质量客观量，可从去噪能力的角度度量去除薄云的效果。其值越大，表示薄云去除效果越好。

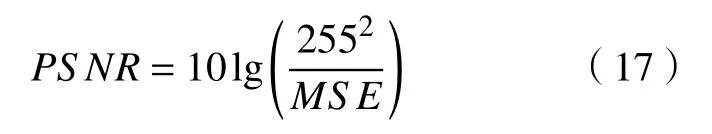
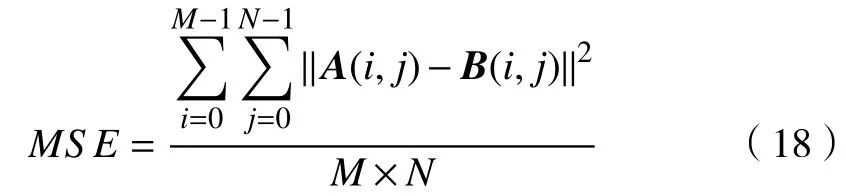
b. 结构相似度SSIM。结构相似度基于人眼视觉，针对图像场景中物体结构属性进行图像质量的客观评价。结构相似度的值越大，表示去除薄云后结构性失真效果越小，效果越好。结构相似度有3个评价因子：

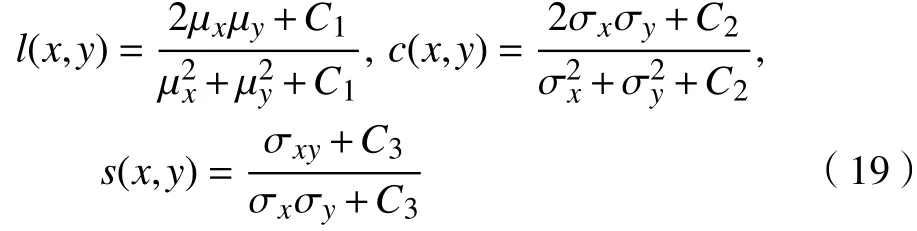
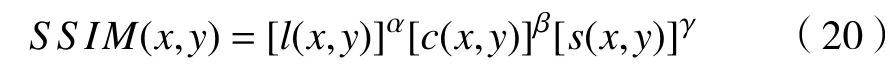
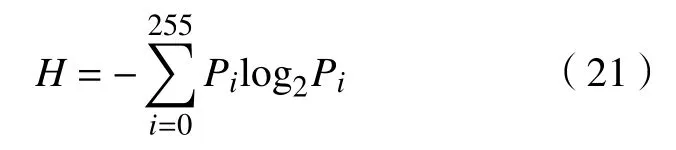
4.2 实验结果及分析

针对4种典型地貌的遥感有云图片（森林区域、山脊区域、道路区域和岩石区域），使用4种不同方法（本文算法、同态滤波、暗元法和小波变换法）进行处理和对比。处理结果对比如图2所示。

图 2 4种不同方法的实验结果图Fig.2 Experiment results with four different methods

从图2的主观视觉效果来看，所采用的几种方法对于去除薄云都有一定的实际效果。无论是对于细节丰富、纹理相似的森林、岩石区域，还是对于边缘轮廓明显、特征相对稀疏的山脊、道路区域，薄云的遮挡都得到了较好的去除。且处理前后图像的失真度较小，效果较为显著。针对不同方法而言，小波变换法对细节信息的保留较好，但有时候会出现亮斑，如在对山脊图像的处理中可见。暗元法增大了图像的对比度，但整体亮度较低，视觉观感上细节不够清晰。同态滤波的薄云去除效果不够明显，纹理信息的显现不太显著。总体而言，本文算法取得了更好的去除效果，不仅去除了薄云的遮挡，使得图像更为清晰，同时保持了原图的完整性，失真较小。同时对比各图可见，本文方法尤其适用于大面积薄云遮挡的遥感图像。综上所述，本文方法具有较强的薄云去除能力，且适用于不同的场景。

以上是从主观的观感角度进行比较，为了进一步分析和说明，采用不同的客观指标进行评价，结果如表1所示。表中组别的1，2，3，4依次代表4种典型地貌（森林区域、山脊区域、道路区域和岩石区域）的图片。

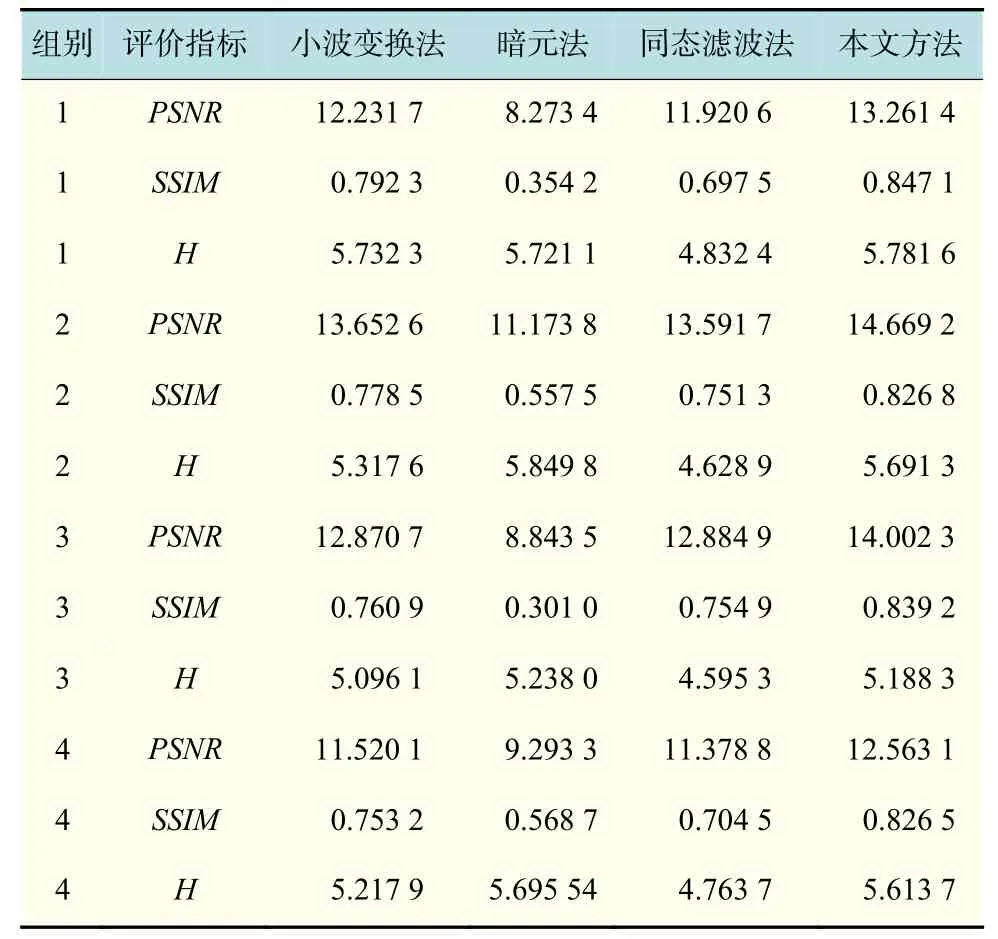
表 1 基于多种评价指标的不同方法去薄云效果比较Tab.1 Indicator-based comparisons between the effects of different cloud removal algorithms

由表1数据可见，本文方法在峰值信噪比和结构相似度上的数值均为最高，说明该方法不仅能够去除薄云遮挡，并且失真度较小，可以很好地保留原图的结构性信息，保持细节信息的完整性。而对于信息熵，本文方法的计算结果高于小波变换法和同态滤波法，也从另一个侧面说明了对图像清晰度的保持较好。相比于暗元法，在对山脊区域、道路区域和岩石区域影像的处理中，本文算法的熵值较小，但在对森林区域影像的处理中，本文算法的熵值较高。可见对于遥感影像的高亮度部分，本文算法更为敏感。多项指标综合而言，本文方法在去除薄云和保留原图细节上都取得了较好的效果。

4.3 实验参数评价

为了更好地说明本文方法的稳定性，以去云后图像的结构相似度为例，对相关参数与实验结果的关系作一定的评价，不同参数对实验结果的影响如图3所示。

图 3 不同参数对结构相似度的影响Fig.3 Impacts of different parameters on SSIM

5 结束语

针对卫星遥感图像受到薄云遮挡，现有方法去除不够彻底或信息丢失的问题，提出了一种利用低秩矩阵分解的处理算法。首先分析了薄云的低秩性，对遥感图像进行低秩分解，去除低秩的薄云部分。然后对前景图像和背景图像进行融合，达到去除薄云，并且保留原图细节信息的效果。通过对不同场景图像利用不同方式进行比对，结果显示，本文方法相比同态滤波、小波变换等方法，能够更好地克服细节损失，同时有效地去除了薄云。本文方法有着广泛的应用前景，如在遥感图像的分类、遥感图像的目标识别、对地观测系统等应用中，均可用该方法对受薄云干扰的图像进行前期去云预处理，具体的实际应用将是下一步的研究工作。