举一反三 论剑中考

倪 波

在学习全等三角形的过程中抓住全等的基本变换及图形特征，可举一反三，触类旁通.例题（2017·天津）如图1，将△ABC

绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD.下列结论一定正确的是（ ）.

A.∠ABC=∠E B.∠CBE=∠C

C.AD∥BC D.AD=BC

【分析】此题考查了全等中的旋转变换，由题意知AB=BD，∠ABD＝60°，可得△ABD为等边三角形，从而可得∠DAB＝60°.又∠CBE＝60°，所以AD∥BC，故选C.

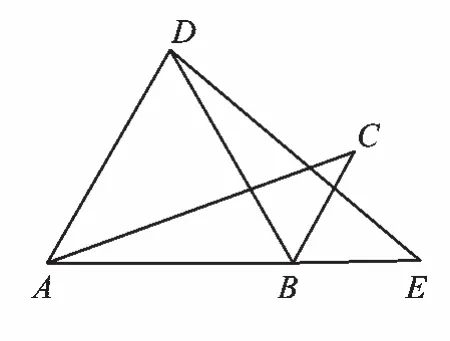
图1

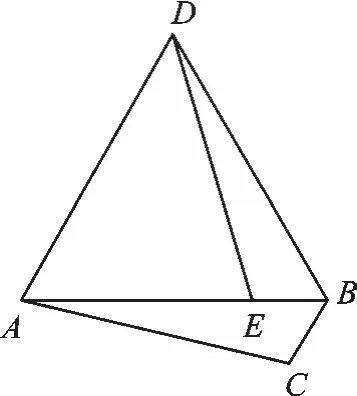
图2

变式1 如图2，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在线段AB上，连接AD，下列结论一定正确的是（ ）.

A.∠ABD=∠AED B.∠CBE=∠C

C.AD∥BC D.AD=BC

【分析】此题将“E点落在AB延长线上”改成“E点落在线段AB上”，图形有所变化，但其本质没有改变，解决思路与例题一样.

变式2 如图3，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD，则AC、DE所夹的锐角的度数为___________.

【分析】此题考查三角形内角和、外角及全等的基本知识，难度不大.答案为60°.

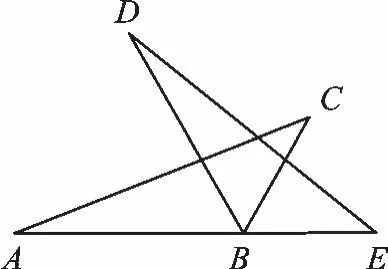
图3

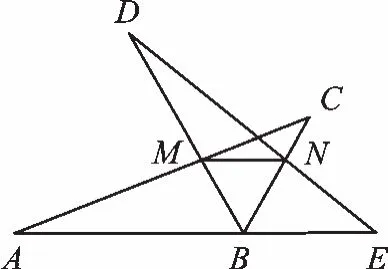
图4

变式3 如图4，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，AC、BD相交于点M，BC、DE相交于点N，连接MN，试判断NM与AE的位置关系，并说明理由.

变式4 如图5，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在线段AB上，AC、DB的延长线相交于点M，BC、DE的延长线相交于点N，连接MN，试判断NM与AE的位置关系，并说明理由.

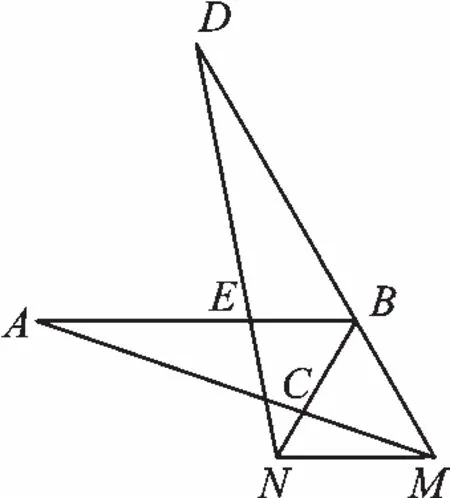
图5

【分析】变式3，根据条件可证△ABM≌△DBN，可得BM=BN.又∠DBC＝60°，可得△BNM为等边三角形，可得∠NMB＝∠MBA＝60°，从而可判断MN∥AE.此题主要考查全等三角形的性质与等边三角形的判定，以及平行线的判定方法等知识，综合性较强.变式4思路与变式3相同，也可以得到MN∥AE.相信一定难不倒你的！