基于CORDIC算法在现场可编程门阵列中正余弦运算的优化实现

张笛， 雷海

(西南交通大学 电气工程学院，四川 成都 610031)

0 引 言

目前，随着中国高速铁路与城市轨道交通的快速发展，对旅客乘车舒适度的要求也越来越高，这就对高速铁路动车组与城市轨道交通车辆的核心部件——大功率变流器提出了更高的要求。因此大功率变流器的控制器逐渐采用现场可编程门阵列(Field Programmable Gate Array，FPGA)作为控制器硬件平台，采用高级硬件描述语言Verilog或VHDL来设计控制器。与传统的DSP控制器相比，基于FPGA的控制器内部是直接硬件电路运算，采用的是并行运行机制，能够在较低频率的系统时钟下实现控制器的快速响应[1-2]。

在大功率变流器的控制器设计中，经常会使用到正余弦运算，目前通常采用“查找表”的方法解决控制器中的正余弦运算问题，但是这种方法导致的一个致命缺陷是占用FPGA芯片的大量存储资源, 而FPGA的基本逻辑单元非常丰富，但是存储资源却非常有限[3]。文献[4～6]介绍了CORDIC算法在正余弦运算中的应用，但是仍然占用较多芯片资源。针对这一问题，本文提出一种改进的基于CORDIC算法的正余弦运算。基于改进型CORDIC算法的正余弦运算不占用FPGA芯片的存储资源，只占用FPGA少量的基本逻辑单元，而且内部运算多为移位与加法运算，非常适合在FPGA芯片中实现。

1 CORDIC算法原理

CORDIC算法可以在圆旋转坐标系、线性坐标系和双曲线坐标系下实现。通过圆旋转坐标系，可被计算的函数的数目受到了限制。通过线性坐标系和双曲线坐标系，可以直接计算更多的函数，如乘法和除法，进而间接计算更多的其他函数，但是系统将变得更加复杂。下面仅介绍算法在圆旋转坐标系下的原理。

1.1 正余弦值计算

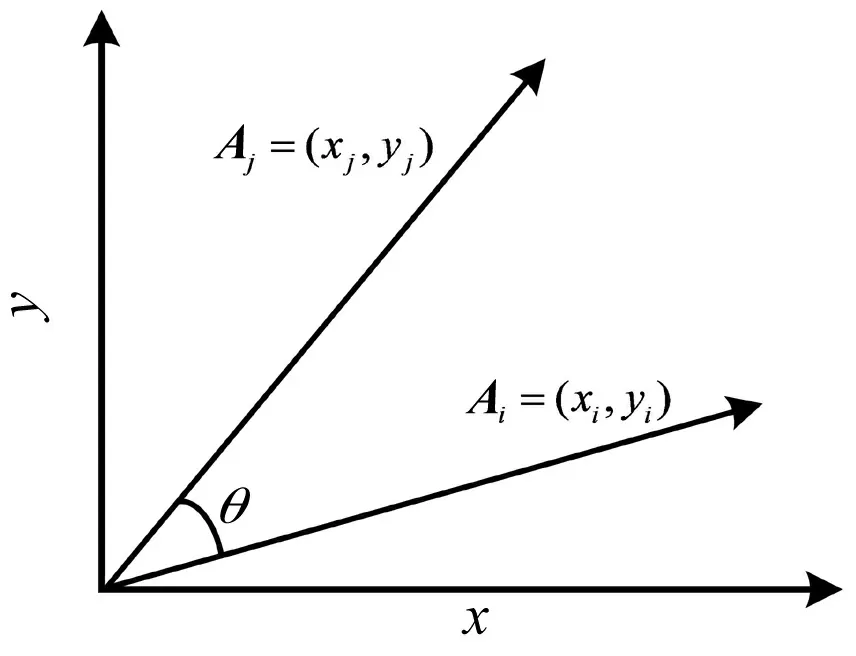
图1 向量旋转

在平面直角坐标系下，一个向量Ai=(xi,yi)旋转角度θ后变为Aj=(xj,yj)，如图1所示。

顺时针与逆时针旋转的旋转矩阵分别为Trs与Ts，如式(1)所示。

(1)

为了便于分析，定义旋转方向函数S为:

(2)

由此可得：旋转矩阵T为：

(3)

向量Ai=(xi,yi)旋转到Aj=(xj,yj)可以表示为：

(4)

这样通过一次旋转就从向量Ai=(xi,yi)旋转到向量Aj=(xj,yj)，如果通过多次旋转，每次旋转一个小角度，最后也能从向量Ai=(xi,yi)旋转到向量Aj=(xj,yj)。第n次旋转一个小角度θn可以表示为：

(5)

将式(5)重新表示为：

(6)

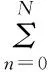
(7)

将式(7)经过n次迭代可得：

(8)

由式(8)可得：

(9)

式中：(x0,y0)即(xi,yi)。设:

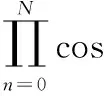
(10)

当N趋于无穷大时，K≈0.607 253。因此由式(9)可知：每次旋转的一个小角度,可以通过简单的移位和相加来实现，这非常适合于用FPGA来实现。通过反复迭代，即可实现向量Ai=(xi,yi)旋转到向量Aj=(xj,yj)。

1.2 正余弦值计算

当设(xi,yi)为(1,0)时，结合式(4)与式(9)可得：

(11)

由式(11)可知：通过设定初始旋转向量为(1,0)，通过多次小角度旋转，最后得到目标向量的横、纵坐标即为相应的余弦值与正弦值。

1.3 误差分析

CORDIC算法中输出向量的误差主要由近似误差和舍入误差构成。把由实际旋转角度与理想旋转角度的误差值引起的输出误差定义为近似误差，该误差是由于旋转级数有限和用来表述角度的进制位数有限引起的。把在每级计算中有限的计算精度引起的误差定义为舍入误差，该误差是由有限的操作数宽度引起的。

令向量vi=(xi,yi)，设向量vi经过n次迭代后得到向量vn=(xn,yn)，实际的旋转角度为zn。则角度误差为：δ=θ-zn。通过迭代，角度误差不会超过最小的基本旋转角度，即：

δ≤arctan2-n+1

(12)

令理想的旋转结果为：

(13)

由此可得绝对误差为：

(14)

相对误差为：

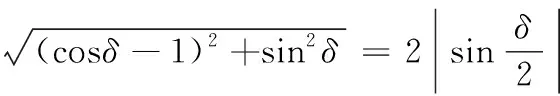
(15)

当n足够大时，arctan2-n+1≈2-n+1，因此最大近似误差gapprox为：

gapprox=2-n+1vn

(16)

由此可见，近似误差主要是由迭代次数来决定的，迭代次数越多，近似误差越小。

vn+1=P(n)vn

(17)

其中

(18)

(19)

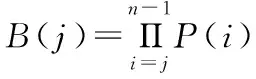
Q[vn]=vn+en

(20)

(21)

由于e(0)=0，所以式(21)可改写为：

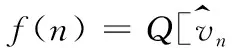
(22)

则最大舍入误差为：

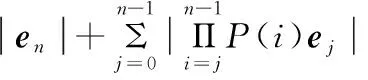
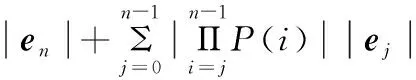
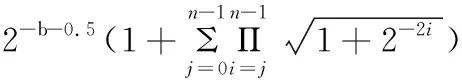
(23)

由此可见，最大舍入误差由操作数的数据宽度b和迭代次数n来决定。数据宽度越宽、迭代次数越少，舍入误差就越小。

2 仿真验证

为了验证改进型CORDIC算法实现正余弦计算的正确性，在MATLAB/Simulink平台上建立仿真模型进行验证，仿真模型如图2所示。

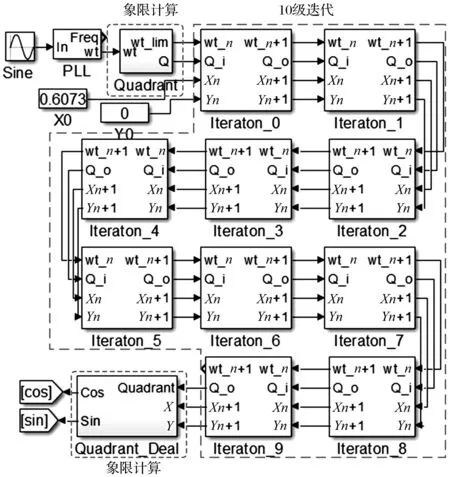
图2 改进型CORDIC算法仿真模型

图3给出了改进型CORDIC算法的正余弦计算仿真结果。图中:sin*与cos*为正余弦信号的原始波形；sin与cos为利用CORDIC算法进行正余弦运算的波形；第三行与第六行为重叠显示的波形。从图3可以看出：基于CORDIC算法进行正余弦运算得出的波形与原始正余弦信号波形完全重合，验证了基于CORDIC算法进行余弦计算的有效性，同时具有较高的精度。

表1给出各级迭代情况下的相位误差仿真结果，可知在10迭代情况下，相位误差仅为0.000 587，可粗略估算出相位误差在0.093%以下，由此可以验证改进型CORDIC算法在进行正余弦计算时具有很高的精度，足以满足大功率变换器控制器运算的要求。

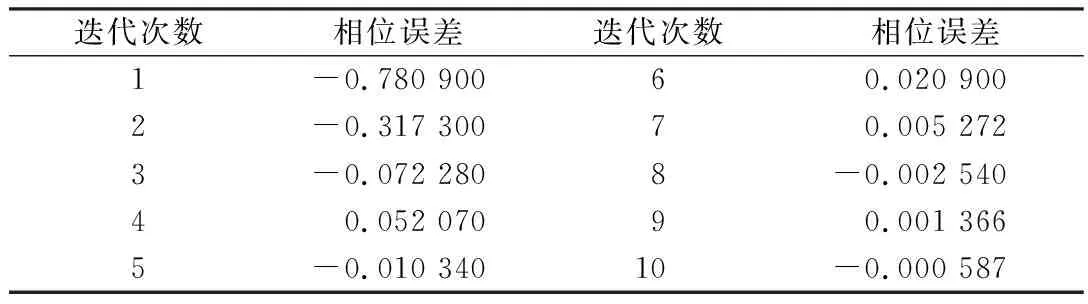
表1 改进型CORDIC算法10级迭代相位误差

3 FPGA优化实现

在本文设计中，进行正余弦计算的改进型CORDIC算法采用10级流水线设计来进行10次迭代，主数据流宽度为12位，具体设计思路如下。

相位信号与主数据流宽度一致，为12位，将高两位处理为相位信号的象限标识，第十位作为相位信号的角度大小，该角度大小在0～90°，通过“象限标识”与“角度大小”可以标识任意相位信号。通过正余弦信号恒等变换构建原始相位信号的输出结果。这样将CORDIC算法的旋转角度范围由传统的0～360°缩小到0～90°，大大降低了迭代级数，只需定义每一级的旋转角度参数(共仅需定义10个)。取消了传统算法中的反正切查找表与对其的访问，从而在取消占用芯片存储器资源的同时，也加快了算法的运算速度。通过“移位”与“加减法”运算设计每一级的迭代运算。每一级迭代首先判断剩余相位信号的正负，然后决定是顺时针旋转还是逆时针旋转，最终目标是使剩余相位向“零”靠拢。

针对迭代过程中移位相加可能出现的溢出情况，本文提出一种新的解决方案：对迭代过程中数据宽度根据符号位扩展1位，取消了传统实现方案中每一步运算中对移位相加的溢出保护电路，进一步降低对芯片逻辑资源的占用。

本文基于FPGA芯片，分别采用查找表方式、传统CORDIC算法、改进型CORDIC算法实现了相位信号的正余弦信号计算电路模块，表2给出了采用相同数据宽度情况下，采用三种算法实现相位信号正余弦计算的芯片资源占用情况，从表2可以看出，改进型CORDIC算法不占用存储空间，仅仅占用少量逻辑资源就可实现较高精度的正余弦信号计算。

表2 资源占用情况

图4是改进型CORDIC算法在FPGA中运行的试验结果，其中:第一行显示为相位信号，采用12位数据宽度，故其值在-2 048～2 047之间，对应实际的相位-2π～2π；第二行与第三行为正余弦计算值，采用12位数据宽度，故其值也在-2 048～2 047之间，对应实际值的-1～1；第四行为CORDIC算法计算的相位误差信号，采用12位数据宽度，试验运行中其实际范围在-1～2之间，由此可以粗略估算出相位误差在0.098%以下。

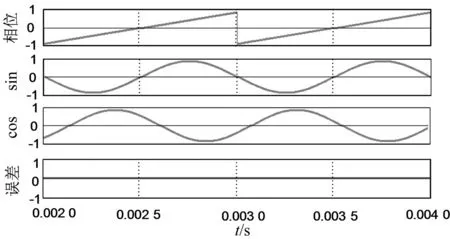
图4 改进型CORDIC算法正余弦计算试验结果

4 结束语

本文针对大功率电力变换器的控制器中使用频率较高的正余弦计算问题，提出一种改进型CORDIC算法。通过仿真验证该算法能够进行正余弦计算，并且具有较高的精度。通过FPGA试验验证，该算法可以在使用较少的逻辑资源的情况下，实现较高精度的正余弦计算，解决了传统方法过度占用控制芯片存储资源的问题，具有较高的应用价值。