基于改进FFT-小波变换的XLPE电力电缆局放降噪方法

任广振， 郑月忠

(1.浙江省电力公司，浙江 杭州 310007；2.国网浙江省电力公司绍兴供电公司，浙江 绍兴 312000)

0 引 言

局部放电(Partial Discharge,PD)是电力电缆安全运行的常见故障，如果不能及时检测出局部放电信号，将会造成安全隐患，严重时可能引发用电事故[1]。PD检测是目前绝缘状态评估的有效方法之一，然而由于运行环境的影响，在实际现场PD信号采集过程中，互感器采集到的信号会含有大量的干扰和噪声[2]93。比如电气设备的热噪声引起的白噪声、由系统载波通信或高次谐波引起的周期性窄带干扰、由可控硅等开关器件动作产生的随机脉冲干扰等[3]。在处理原始信号时，只有将混杂的噪声加以消除或抑制后，PD信号的一些特征才能显现出来[4]。

目前在噪声干扰的抑制方面研究较多的方法是小波变换[5-6]。小波变换由于具有多分辨率分析的特点，在处理局放这类非平稳信号时能取得较好的效果，但是针对周期性窄带噪声进行去噪时，往往会导致波形失真或者去噪不彻底。文献[7]利用小波变换中的S变换分辨湮没在噪声中的PD信号，引入幅度和宽度均随频率变换的高斯窗，可提取局放脉冲发生时刻及信号中心振荡频率等特征信息，但S变换并不能在噪声中准确还原出PD信号波形。文献[8]利用小波包分解技术对PD波形数据进行去噪，在PD信号受干扰程度较小时去噪效果较好，而在实际测量中，所获得的PD信号常常受到较大的干扰，因此导致去噪不彻底。文献[9]提出基于插值细分法的二代小波包，对电缆在线监测中受噪声干扰的PD信号进行去噪处理，提高了PD信号的信噪比，但波形畸变仍然较大。另一方面，针对周期性窄带噪声，文献[10]采用快速傅里叶变换方法，使用局部能量比法对PD信号去噪，结果表明傅里叶分析法对窄带干扰有很好的抑制效果，但对白噪声去除效果并不明显。

针对传统小波分析去躁算法存在的信噪比低、波形畸变率较大和还原准确性不高的问题，采用了快速傅里叶变换与小波算法结合进行综合去噪。该方法首先利用基于遗传算法的模糊C均值聚类算法对快速傅里叶变换进行阈值优化选取，从而抑制周期性窄带噪声，减小了波形畸变率。然后，再通过小波变换，去除白噪声，提高了去噪结果的信噪比。仿真结果表明，所提出方法不但可以很好地抑制窄带干扰，而且能够去除白噪声，去噪效果优于传统小波去噪算法。

1 基于改进FFT的PD信号降噪方法

1.1 快速傅里叶分析

针对周期性窄带干扰在频域上能量集中的特点，在进行小波去噪之前使用快速傅里叶分析法去除周期性窄带干扰。设信号f(t)的快速傅里叶变换为F(ω)，则FFT功率谱为:

(1)

由于周期性窄带干扰频带窄且相对于PD信号能量较大，染噪信号在快速傅里叶变换功率谱上表现为幅值很高的干扰峰。只需找出干扰峰的位置，对其做适当的压缩处理即可达到抑制周期性窄带干扰的目的。

1.2 基于AGFCM聚类算法的干扰峰定位方法

本文采用基于遗传算法的模糊C均值聚类算法来定位干扰峰。模糊C均值(Fuzzy C-means,FCM)聚类算法通过迭代优化得到每个样本点对所有聚类中心的隶属度，从而确定聚类数据点归属，以达到自动对样本分类的目的[11]。但传统FCM存在诸多问题，如算法对初始聚类中心敏感、收敛速度慢和易陷入局部最优等。本文采用基于遗传算法的FCM聚类算法(AGFCM),利用Agnes层次聚类算法选取 FCM的初始聚类中心，并利用遗传算法进行优化。首先采用Agnes层次聚类算法，从全局数据集中按比例进行抽样得到全局数据集的一个子集。再通过设置聚类个数c进行层次聚类直到产生c个FCM最终聚类中心。然后将这c个FCM聚类中心，作为遗传算法的初始种群。再对这c个种群个体进行选择、交叉和变异操作，经过M次迭代后，实现对数据聚类的优化。

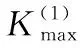
(2)

式中:α为裕度系数，用于保护受窄带干扰较小的功率谱部分。

1.3 FFT-小波算法的具体步骤

(1)使用式(1)求得时域信号f(t)的功率谱P(ω)。

(2)使用AGFCM算法对染噪信号功率谱数据分为两类，选取受窄带干扰影响较小的一类的最大值为阈值T，以定位窄带干扰峰，并对定位到的干扰峰进行压缩处理。

(3)对滤除窄带干扰峰后的P(ω)进行FFT反变换，得到去除窄带噪声后的信号g(t)。

学风不正首先带来的就是文风不正。据媒体报道，今年5月31日至6月30日，中央第一环境保护督察组对河北省第一轮中央环境保护督察整改情况开展“回头看”。督察人员发现，河北省唐山市芦台经济开发区和高新区在接到督察反馈意见后，并没有认真研究，而只是将别人的整改方案照抄照搬，简单复制了事，明显存在消极应付现象。

(4)对g(t)进行小波变换分析，选取母小波，确定阈值，滤除白噪声，得到最终去噪信号。

2 仿真案例

2.1 PD信号仿真模型

在理论研究中，通常采用4种数学模型来模拟纯净的PD信号[2]95：

单指数衰减形式：

(3)

双指数衰减形式：

(4)

单指数衰减震荡形式：

(5)

双指数衰减震荡形式：

(6)

式中：A为信号幅值；τ为衰减系数，取0.1 μs；fc为震荡频率。

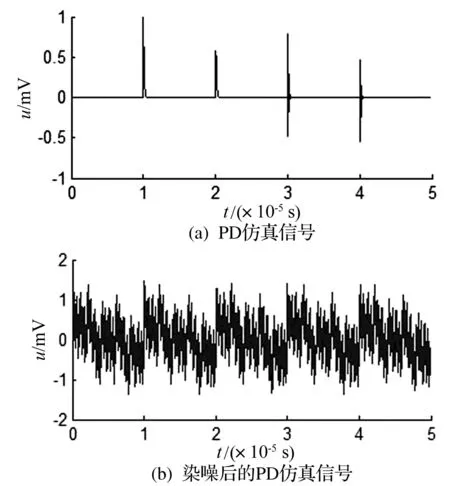
图1 模拟染噪前后仿真信号

对PD信号进行加噪处理，加入满足高斯分布N(0,0.022)的高斯噪声。叠加上不同频率的周期性窄带干扰以模拟现场环境中的混频窄带干扰。干扰频率设为100 kHz、200 kHz、500 kHz，1 MHz、2 MHz、5 MHz、10 MHz、20 MHz。原始PD信号和染噪信号分别如图1(a)、图1(b)所示。

2.2 信号的快速傅里叶变换功率谱特性

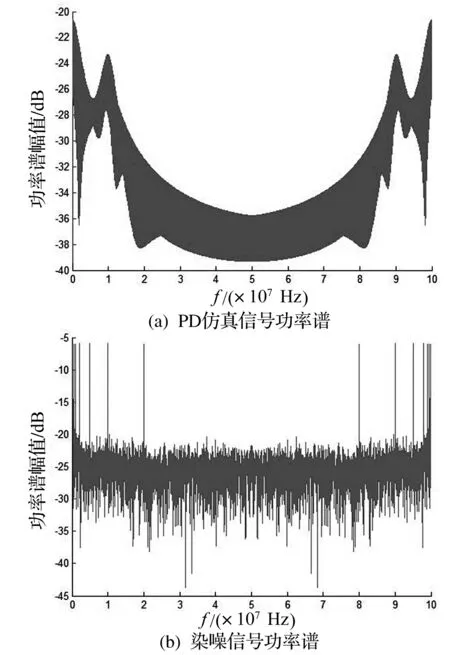
图2 快速傅里叶变换功率谱

PD仿真信号及染噪信号的FFT功率谱如图2所示。比较图2(a)和图2(b)可以发现，当叠加上窄带干扰后，信号的功率谱在各干扰频率处出现了强度明显大于原始PD仿真信号的干扰峰。从图2进一步可见，存在窄带干扰和白噪声干扰时，信号的功率谱会出现幅值很高的干扰峰和细小的干扰毛刺。

2.3 染噪信号功率谱中干扰峰定位

从染噪信号的FFT功率谱中可以看出，功率谱中元素分为两类，一类是窄带干扰对应的干扰峰，其幅值很大，另一类则幅值偏小。根据干扰峰的这些特点使用AGFCM聚类算法将两种元素分类，根据式(2)计算出阈值，进而找出干扰峰，进行压缩处理。取裕度系数α为1.2，得到预处理波形。

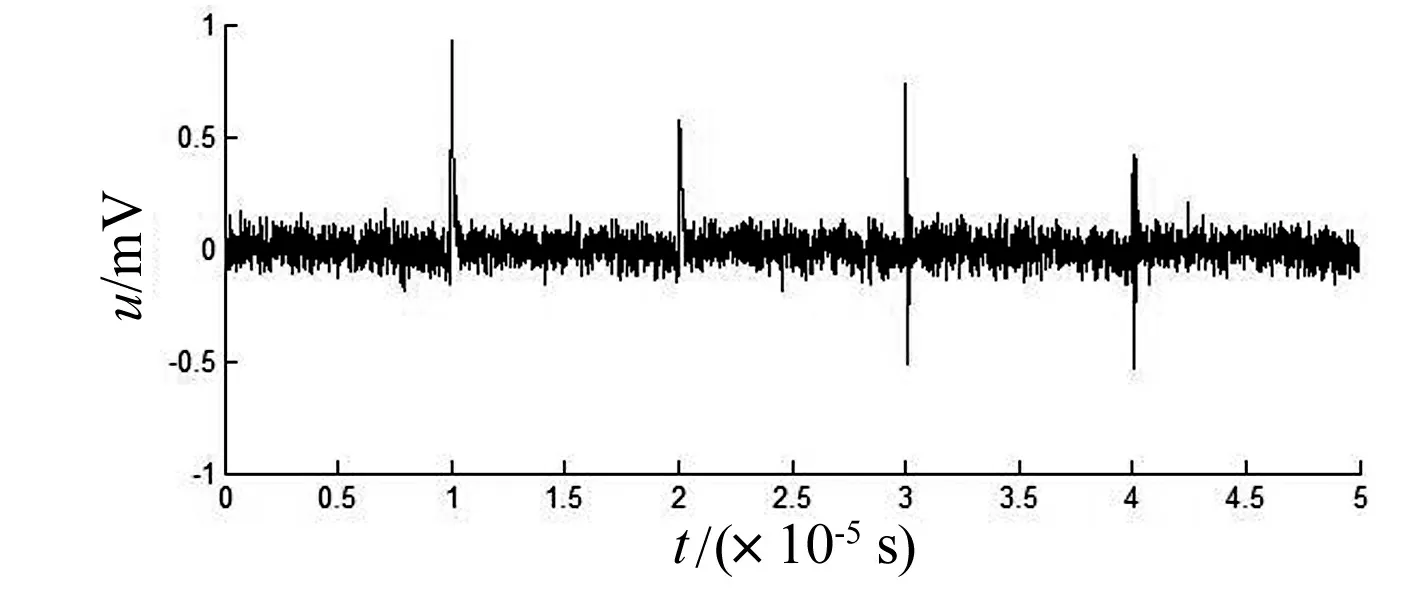
图3 改进FFT处理后波形

从图3可以看出，窄带干扰得到很好的抑制，剩余干扰主要为白噪声干扰。这将由小波变换来处理。

2.4 小波分析去除白噪声

图4 FFT-小波综合去噪后波形

考虑小波与被分析信号的相似程度，使用db2小波对染噪信号进行6层小波分解，采用SURE软阈值，去噪结果如图4所示。

综合比较图4和原始PD信号波形图1(a)，可以看出，综合去噪后的波形基本保持了原波形特征，且噪声基本滤除。

3 去噪效果评价

图5 各去噪方法对比

为了与本文提出的方法做比较，分别采用db2和db8小波去噪算法与其进行对比。对于小波去噪算法，选用的母小波是db2和db8,采用的阈值是SURE原则，分解层数为6层，如图5所示。

图5与图4比较，可以看出3种方法均可以将PD信号从噪声中提取出来。图5中PD信号衰减幅度均大于图4，且图4无论从信号的波形上，还是从保留的信息量上来看，都比图5要好，说明FFT-小波去噪算法有一定的优越性。

为了定量地评价去噪效果，本文从信噪比 (SNR)、幅值误差(MSE)和波形相似系数(NCC)3种不同的指标全方位进行比较。信噪比和幅值误差是从宏观上衡量去噪的效果，信噪比越大，幅值误差越小，说明去噪效果越好。波形相似系数是从微观上衡量去噪的效果：其值在(-1,1)之间,-1代表变换前后波形反向；0代表两波形正交；1代表完全相同。波形相似系数越接近1，说明波形畸变的越小，去噪效果越好。表1给出了不同去噪算法在3个评价指标上值的大小。

表1 3种去噪方法评价指标

由表1可以看出，db8小波去噪比db2小波去噪SNR高约70.2%，MSE低约25%，NCC高约17.5%。说明只使用小波去噪方法时，db8小波比db2小波去噪效果好，且波形畸变较小。而本文提出的FFT-小波综合去噪方法与db8小波去噪相比，SNR高约152.2%，MSE低约73.35%，NCC高约25.45%，可以看出，FFT-小波综合去噪方法各方面均优于小波去噪算法。

4 结束语

本文针对传统小波变换去噪算法信噪比不足、波形畸变率较大的缺陷，采用改进FFT结合小波变换算法对信号综合去噪。通过分析噪声特点，利用窄带噪声在功率谱上能量集中的特点，采用AGFCM聚类阈值法对传统FFT去噪算法进行了改进，并结合小波变换，对染噪信号进行综合去噪。最后通过和单一小波去噪方法对比，使用信噪比、波形相似系数和均方误差3种指标对不同方法去噪结果进行客观评估。结果表明，本文提出的FFT-小波去噪算法去噪效果信噪比高，波形畸变较小，优于传统小波算法。