基于散体力学的斗轮堆取料机挖掘阻力研究

上海海事大学物流工程学院 上海 201306

1 研究背景

斗轮堆取料机是散货堆场重要的装卸设备，在工作时若发生物料坍塌、掩埋铲斗等非正常工况，会造成取料过程中铲斗挖掘阻力瞬时增大，对整机结构安全及使用寿命造成较大影响。笔者应用散体力学中的离散单元法（DEM）分析处理这一问题，建立铁矿石物料模型与斗轮堆取料机挖斗模型，通过EDEM软件分别计算正常挖掘和危害工况下的阻力值，为后续研究斗轮堆取料机疲劳和损伤提供基础数据，并对传统经验公式提出优化建议。

2 挖掘力学模型

以某铁矿石码头斗轮堆取料机为研究对象，在确定取料挖掘阻力的力学模型时，作以下假设：① 将物料视为均质的、连续的，不具备可压实性的介质[1]；②将挖掘过程简化为二维平面问题，所研究的挖斗属于宽型料斗，认为挖掘阻力与挖斗宽度成正比[2]；③ 忽略物料颗粒粒度大小对挖掘阻力的影响；④对挖斗上的铲齿、侧刃、护口等配件进行适当简化。挖斗侧面简化前后如图1所示。

建立如图2所示挖掘力学模型。挖斗外滑移面和挖斗内滑移面与挖斗运动轨迹切向的夹角分别为滑移角ω、v，两个滑移面间的夹角为φ，挖斗运动方向与水平面的夹角为θ，VC为挖斗运动切线方向。作用于挖斗上的力共有五个，分别为两滑移面上的反力NAB、NAC，黏聚力 τAB、τAB，以及物料重力 W[3]。

在挖掘过程中，物料始终沿挖斗内壁滑移角ω向挖斗进料。在整个过程中，斗内滑移角ω持续加大，斗外滑移角v逐渐减小，且两者的和不变[4]。物料挖掘过程中滑移角ω的变化过程如图3所示。

3 挖掘阻力分析

挖斗取料过程的挖掘阻力由提升阻力、充填阻力、惯性阻力及摩擦阻力组成。提升阻力指推动物料在运行轨迹上的切向分力。充填阻力指挖斗外滑移面上物料黏聚力及反力在运行轨迹上的切向分力。惯性阻力指物料惯性力在运行轨迹上的切向分力。摩擦阻力指的是物料与挖斗之间的摩擦阻力[5]。

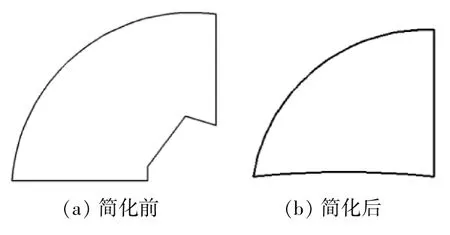
▲图1 挖斗侧面示意图

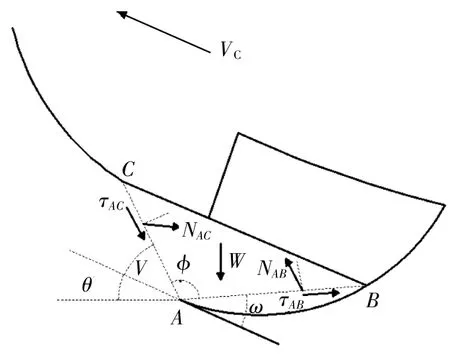
▲图2 挖掘力学模型

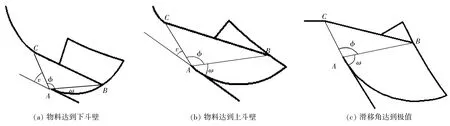
▲图3 物料挖掘过程中滑移角ω变化示意图

3.1 苏联经验公式

苏联经验公式将挖掘阻力分成两个阶段进行分析，第一阶段是挖斗刚插入物料的阶段，第二阶段是挖斗插入物料一定深度后准备提升的阶段[6]。根据规律，挖斗在第二阶段出现最大挖掘阻力，随着挖斗的旋转，阻力渐渐变小。计算最大挖掘阻力P的苏联经验公式为：

式中：LBH为挖斗插入料堆的深度，m；B为挖斗宽度，m；KC为物料剪切应力，Pa。

3.2 国内学者公式

国内学者应用改进过的挖掘机模型和变形斗轮进行试验，得出另一种计算公式[7]，最大挖掘阻力P为：

式中：fL为单位长度挖掘阻力，指1 cm挖掘长度上所需的挖掘力，N/cm；L为挖掘边总长度，cm。

式（2）需要求解挖掘过程中挖掘边的总长度L，然而在挖掘作业时，挖斗与物料接触的挖掘边长度是不断变换的。苏联经验公式和国内学者公式都是基于试验得出，考虑了挖料的动态过程，简化了参数的选择。

4 EDEM软件仿真

4.1 物料颗粒、物料堆和挖斗模型

物料颗粒形状由多个大小球体连接组成[8]。铁矿石主要形态为球形、块状形、细条形和圆锥形等数种。使用不同大小的筛子对作业中的颗粒进行筛分，总体服从高斯分布原理，设定物料粒径分布状况，见表1。

表1 物料粒径分布

铁矿石和钢铁的物理性质见表2。铁矿石自身间的静摩擦因数为0.6，滚动摩擦因数和恢复因数分别为0.01、0.5。铁矿石与钢铁间的上述三项因数依次为1.2、0.01 和 0.42[9]。

表2 铁矿石和钢铁物理性质

仿真挖掘过程中主要对物料堆上侧进行挖掘，对料堆底部的物料影响很小，因此适当减少尺寸，简化计算，简化为一个高6 m、长8 m、宽2 m，静止角为37°的斜梯形铁矿石料堆。在结构正确的基础上简化挖斗。由于是侧卸式卸料，斗轮与地面垂直线夹角为8°[10]。简化后料堆和挖斗模型如图4所示。

▲图4 简化后料堆和挖斗模型

4.2 挖料轨迹

挖料轨迹是一条复杂的曲线，由三种运动组合而成[11]，分别为：① 基于斗轮机轴心的圆周运动，即斗轮的旋转运动；②回转运动，即斗轮机头随回转轴承中心摆动，其回转半径长度为悬臂皮带机至回转轴承中心的长度；③进料的直线运动。

5 仿真结果分析

5.1 阻力计算

苏联经验公式中最大挖掘阻力P发生在挖斗即将提升的时刻，设参数LBH=1.1 m，B=0.65 m，KC=30 000 Pa，代入式（1），解得 P=47 190 N。

国内学者公式中选取单位长度挖掘阻力fL为300 N/cm，切割深度比α为1.57，挖掘高度与斗轮半径之比C为1，挖斗容积J为0.73 m3，机头半径R为3.75 m，松散因数f为1.4，机头旋转角度φ0为90°，斗轮机斗数 Z为8，圆角修正因数km为 1.49，从而求出挖掘边总长度L和最大挖掘阻力P：

5.2 EDEM仿真分析

首先在1 s内快速生成斜梯形物料堆颗粒，在颗粒填满后，设置2.3 s的静止时间，使颗粒恢复到静止状态，再进行挖掘动作仿真，从而保证仿真的正确性。

挖掘物料的厚度、挖掘速度、斗内物料体积都是影响挖掘阻力的重要因素，将挖斗扫过物料堆体积的比例作为仿真的重要参数。经过多次仿真，发现挖斗扫过物料堆体积的比例在70%～80%时，可以视为挖掘正常工况，超过80%则视作挖掘危害工况。挖掘正常工况阻力值变化曲线如图5所示。从图5中可以看到，挖掘阻力随挖掘角度的增大而增大，当斗轮扫过80%时，最大值为47 851.9 N。

▲图5 挖掘正常工况阻力变化曲线

5.3 三种计算方法结果对比

由苏联经验公式可知，阻力值随着挖斗的插入逐渐增大，最大值发生在挖斗准备提升的时刻，随后阻力值随着斗轮提升而减小，从图5中可以看出这一过程。

苏联经验公式挖掘阻力值相对于国内学者公式而言较大，这是因为苏联经验公式采用的是大型装载机械，导致计算值偏大。国内学者公式挖掘阻力值正好位于EDEM仿真求解出的阻力值40 770.7～47 851.9 N范围内，与实际工作中斗轮堆取料机工况相仿，所以将所得阻力值视为正常挖掘最大阻力值。

综上所述，三种不同方法得出的最大挖掘阻力值基本一致，说明了模型及基于DEM和EDEM软件求解的可行性。

5.4 危害工况挖料过程

超80%时为危害工况。当挖斗全部埋入物料堆，即挖斗扫过物料堆的积达到100%时，其阻力的变化曲线如图6所示。由图6可见，最大阻力值为84 382.7 N，几乎是正常最大挖掘阻力值的2倍，其在最高点维持时间为0.1 s。

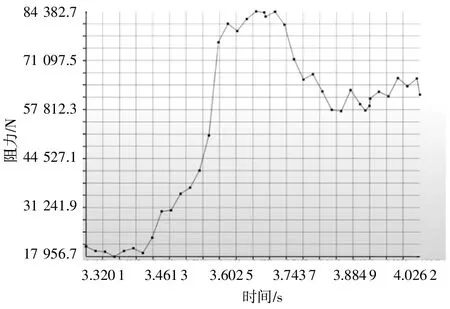
▲图6 挖掘危害工况阻力变化曲线

按照同样的方法对扫过物料堆体积60%、90%和低于50%的工况进行分析，整理后得到的最大阻力值，见表3。

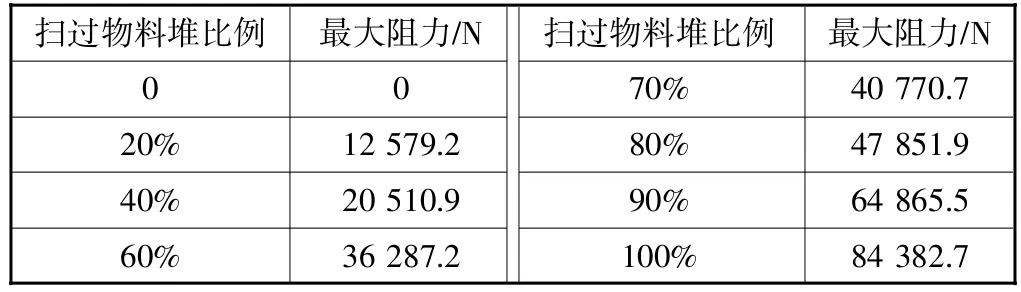
表3 扫过物料堆时最大阻力

为了体现不同比例对挖掘阻力的影响，将表3中的数值除以正常挖掘阻力值44 416.83 N，在MATLAB软件中拟合出危害工况因数曲线，如图7所示。从图7中可以看出，前期阻力值变化缓慢，类似于线性直线段，后期阻力曲线逐渐陡峭。

拟合出的危害工况因数曲线公式为：

式中：x为挖斗扫过物料堆的百分比。

6 结束语

笔者建立斗轮堆取料机挖掘过程力学模型，采用EDEM软件仿真分析，并与理论值相验证，对不同比例下挖斗扫过的物料堆体积进行研究，得到如下结论。

（1）斗轮堆取料机正常挖掘时，应控制斗轮扫过物料堆体积在70%～80%之间。

（2）当物料堆突然塌陷，挖斗全部埋在物料堆时，最大阻力值约为正常阻力值的2倍，维持时间为0.1 s。

（3）拟合出危害工况因数曲线，为后续研究疲劳损伤提供数据基础。

▲图7 危害工况因数曲线