3-PRR并联机器人机构运动学建模与分析

，，，

(1.山东科技大学 机械电子工程学院，山东青岛 266590；2.青岛大学 数据科学与软件工程学院，山东 青岛 266071)

并联机构具有刚度质量比大、精度高、承载能力强、易于实现高速等特点[1-3]。平面三自由度并联机构在芯片封装及电路板精密切割等领域具有较广的应用，已逐渐成为国内外研究热点。

目前国内外在平面三自由度并联机构的运动学、优化设计和刚度分析等方面做了一些研究工作[4-6]。张宪民等[7-9]研究了3-RRR和4-RRR机构的运动学性能。Mousavi等[10]研究了3-RPR机构的最大奇异椭圆平面及优化分析。Staicu[11]研究了3-PRR机构的运动学分析及运动控制。董倩文等[12]对3-PRP机构做了运动学灵巧度和刚度分析。李树军等[13]分析了3-PRR机构的刚度特性。韩霄等[14]对3-RRP机构做了运动学、动力学及精度分析。王鑫辉等[15]对3-PRR机构做了多目标拓扑优化设计及灵敏度分析。以上学者分别对不同构型的平面并联机构做了研究，但是目前尚没有对3-PRR机构进行系统的运动学数学建模和运动特性分析，这是对此构型机构进行运动控制与优化设计的基础。因此，本研究针对3-PRR平面并联机器人机构，建立运动学正反解数学模型，分析不同姿态角对工作空间的影响。利用机构的雅克比矩阵条件数、最小奇异值、可操作性三个指标对3-PRR并联机构进行灵巧度分析。

1 3-PRR并联机构运动学建模

1.1 运动学反解

运动学反解建模分析是已知动平台中心Oa的位姿(x,y,φ)，求解出驱动副的输入li,li为驱动杆AiBi的杆长。

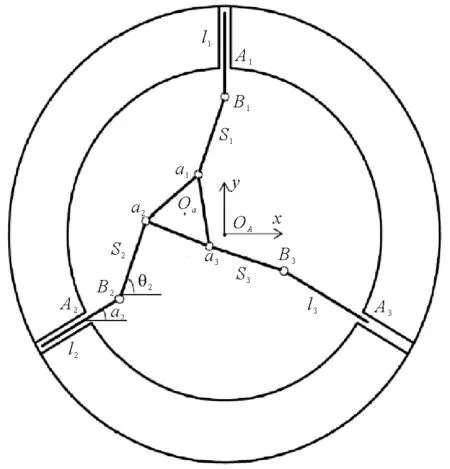
图1 3-PRR并联机构模型简图(P:移动副，R:转动副)Fig.1 Model diagram of 3-PRR parallel mechanism(P:Moving pair,R:Rotating pair)

3-PRR并联机构模型，见图1。由图1可知，3-PRR并联机构由定平台、 动平台和三条对称的支链组成，每个支链包括主动杆和从动杆，主动杆通过移动副与定平台连接，随着主动杆的伸缩，该机构可实现平面内三自由度运动。并联机构的定坐标系(定系)和动坐标系(动系)的原点分别位于三角形A1A2A3和三角形a1a2a3的中心。

1.1.1 位置分析

每条支链驱动杆长度为li(i=1～3)，从动杆长度为Si，动平台外接圆半径为r，定平台外接圆半径为R，其中li和Si与定系的水平轴的夹角分别为αi和θi，ai与动系的水平轴的夹角为βi。动平台中心坐标Oa在定系下可表示为

Oa=x,y,φT。

其中：x和y为定系下动平台中心坐标，姿态角φ为动系相对于定系的转角。

对于支链i，建立运动学方程如下所示：

(1)

其中：

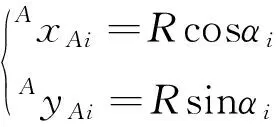
运动学方程(1)整理可得：

(2)

基于三角函数定理，消去从动杆的转角θi可得

(3)

求出驱动杆长度为：

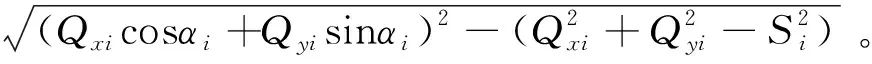
(4)

1.1.2 速度分析

将运动学方程(2)对时间求一次导数，得到速度方程：

(5)

方程(5)写成矩阵形式为：

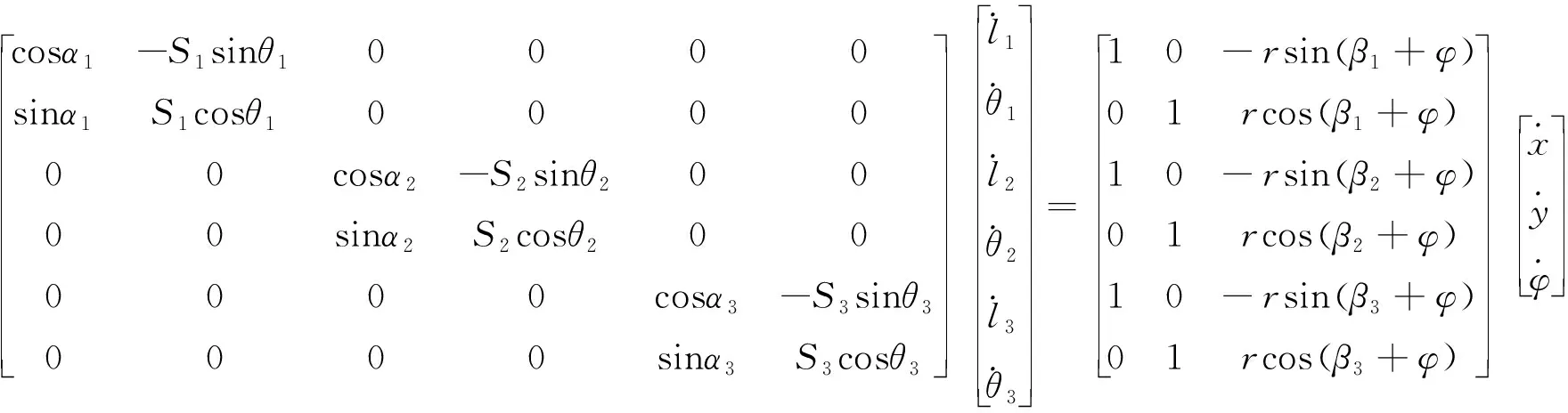
(6)

简记为

(7)

1.1.3 加速度分析

公式(5)对时间求导，可得加速度反解方程为

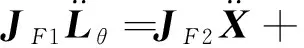
(8)

其中：

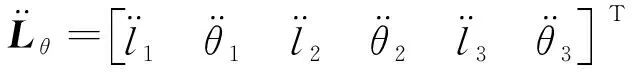
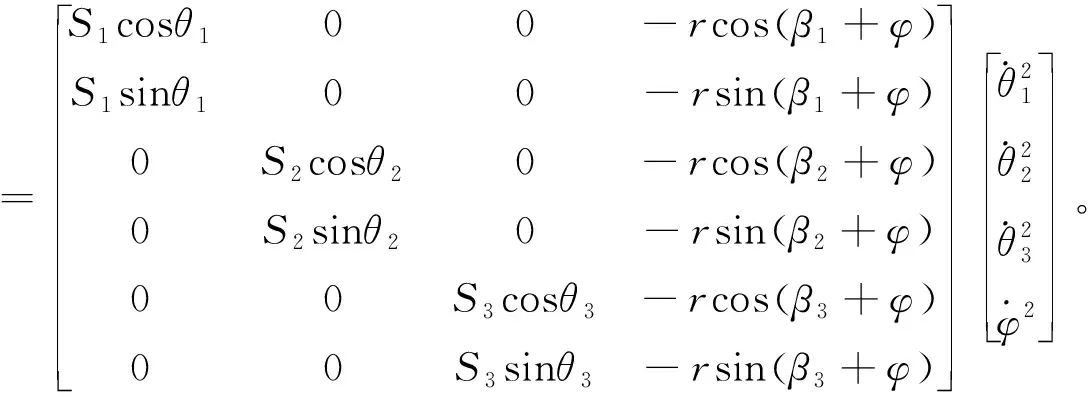
1.1.4 算例分析

机构动平台中心分别按照0°和30°姿态角沿一个半径为30 mm的圆形轨迹运行，以轨迹的圆心为坐标系原点。基于机构的反解方程，通过Matlab数值计算得到0°和30°姿态角下的杆长、速度和加速度曲线，如图2和图4所示；Adams仿真曲线图如图3和图5所示。

通过对比图2和图4可知，在改变动平台姿态角时，对驱动杆的杆长变化影响较大，但对驱动杆的速度和加速度影响较小。通过对比图2和图3、图4和图5可知，各驱动杆的长度、速度、加速度曲线变化平滑，Matlab计算结果与Adams仿真分析结果基本一致，验证了运动学建模的正确性。

1.2 运动学正解

运动学正解的坐标系建立及符号参数表示与运动学反解的相同，在此不再赘述，运动学正解方程如下：

(9)

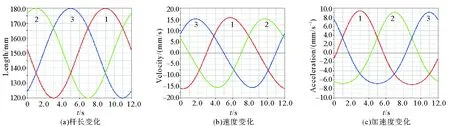
图3 姿态角0° Adams仿真曲线图Fig.3 The simulation curve of 0 degrees of attitude angle by Adams

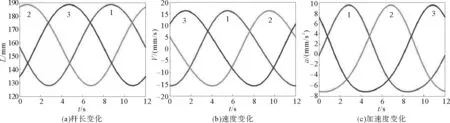
图4 姿态角30° Matlab计算曲线图Fig.4 The calculation curve of 30 degrees of attitude angle by Matlab

图5 姿态角30° Adams仿真曲线图Fig.5 The simulation curve of 30 degrees of attitude angle by Adams

同理可得，速度正解矩阵方程为：

(10)

简记为

(11)

速度正解方程(10)对时间求一次导数，得到加速度正解矩阵方程如下：

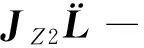
(12)

其中：

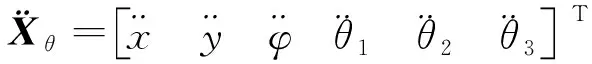
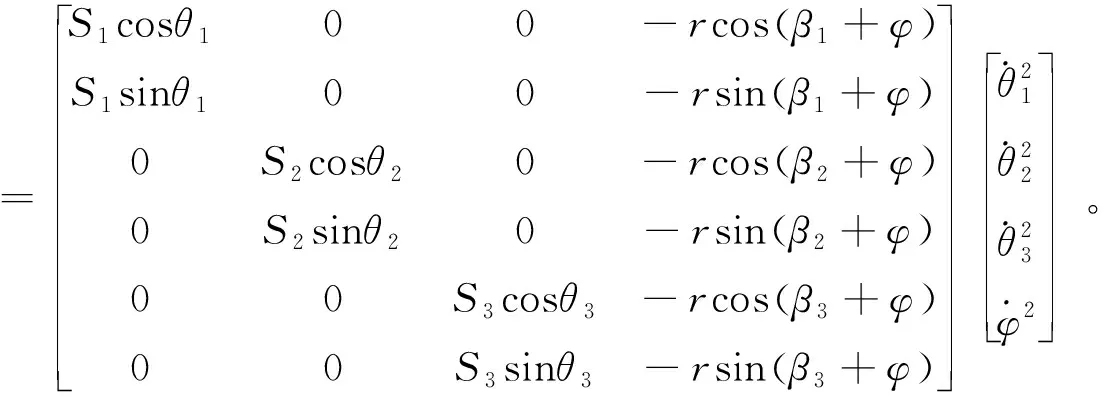
2 3-PRR并联机构工作空间分析

2.1 工作空间及面积求解

2.1.1 约束条件

在约束条件下，根据运动学方程是否存在实数解，可以求解出3-PRR机构的可达工作空间，有实数解的点即为机构的可达工作点。已知3-PRR并联机构参数：S1=S2=S3=200 mm,r=50 mm，R=400 mm。求解本3-PRR并联机构工作空间：即在满足以下约束条件下，计算求解动平台中心点Oa可达工作点的集合。工作空间的约束条件：

1) 各驱动杆的长度限制：并联机器人由移动副驱动,驱动杆长度变化须满足

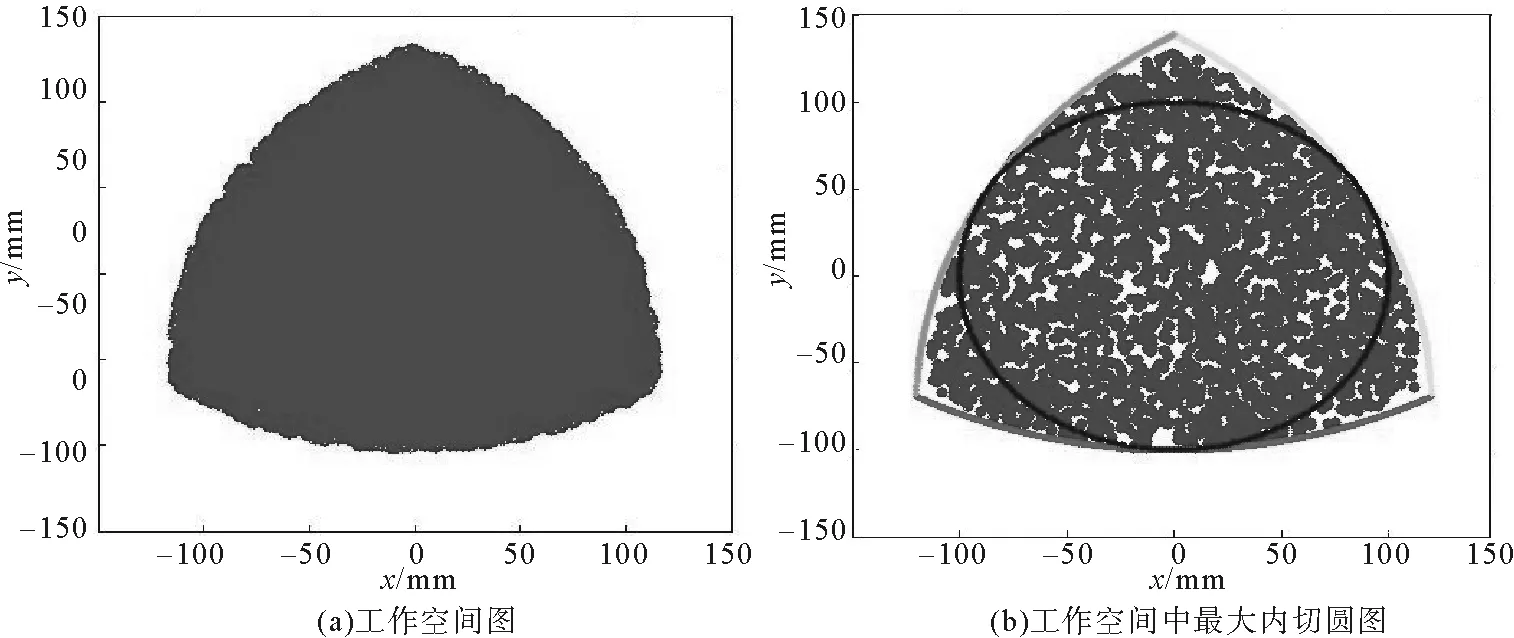
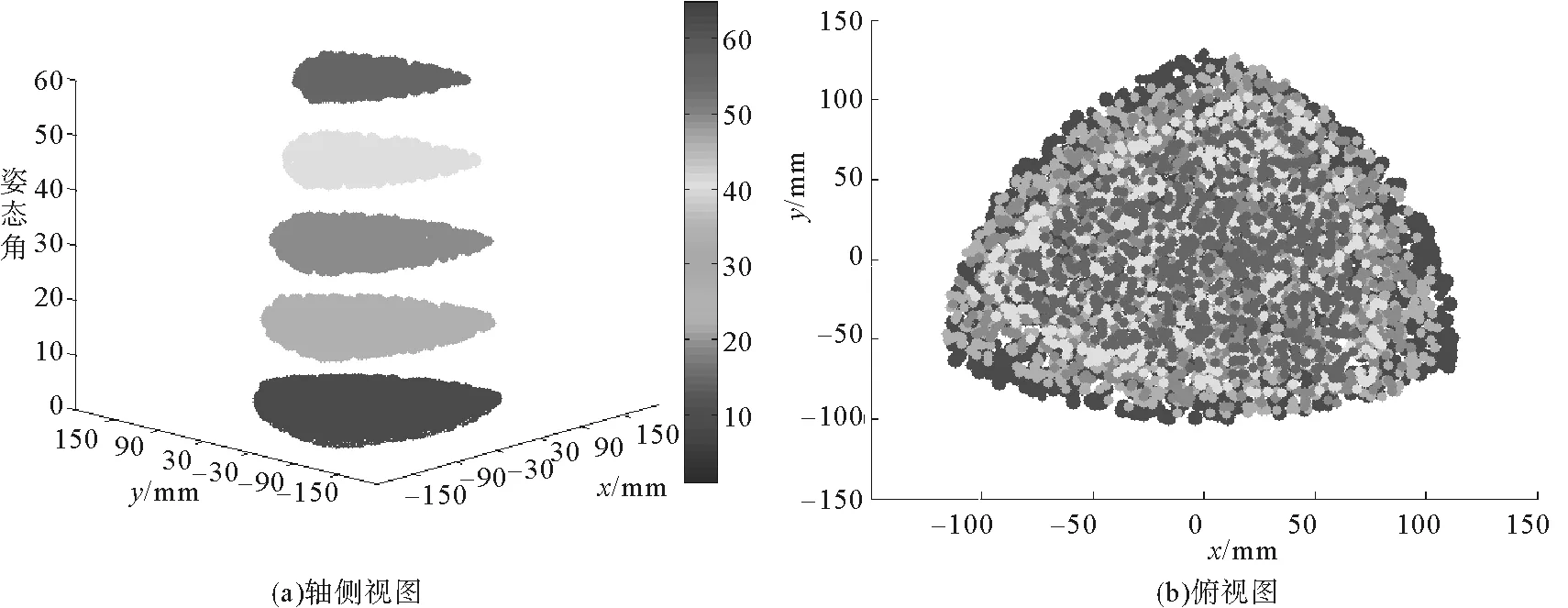
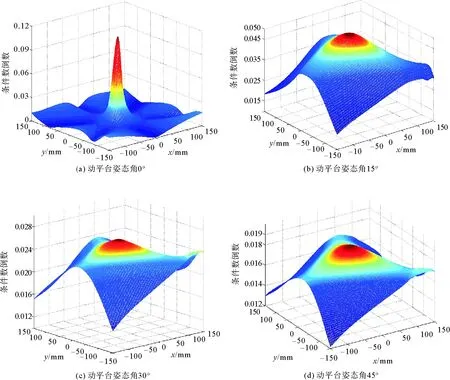
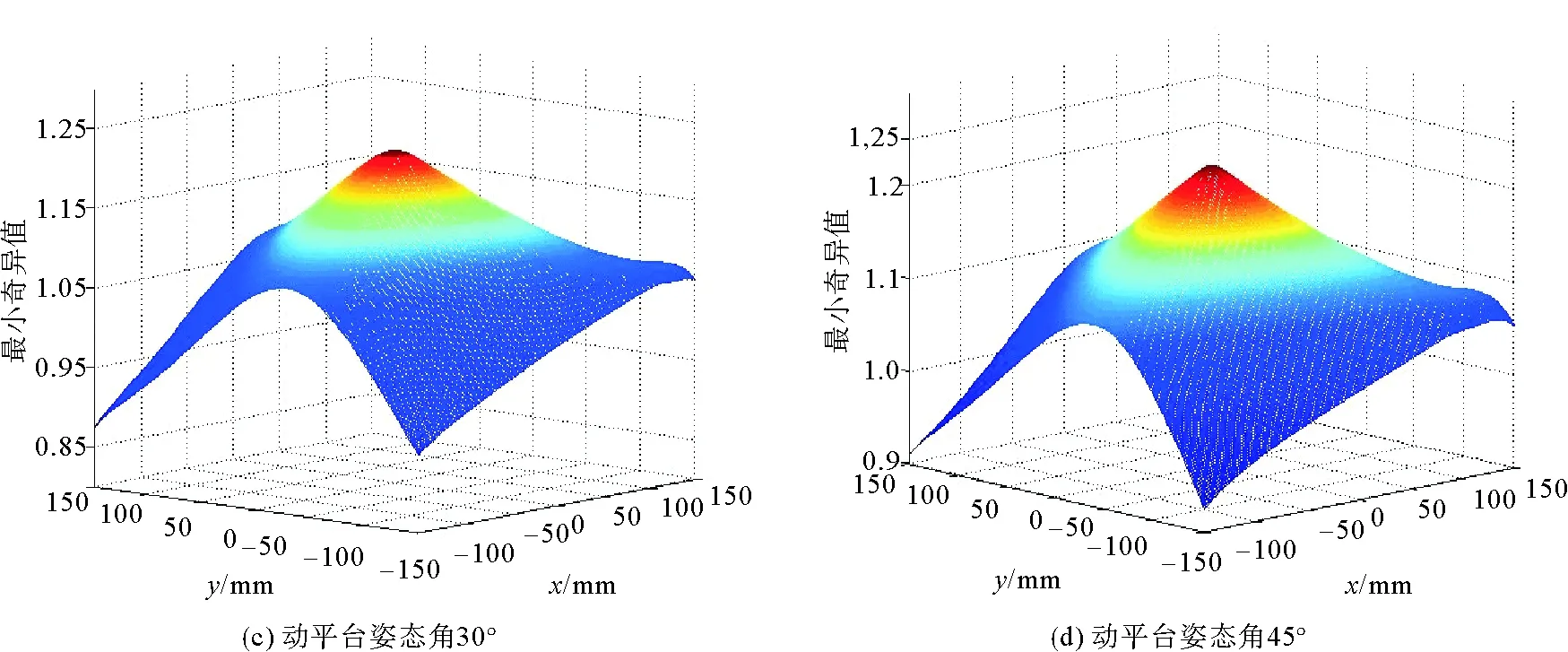
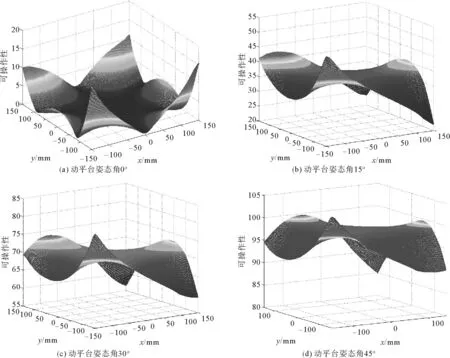
lmin

当某一驱动杆长达到其极限值时，并联机器人动平台上的中心点也就达到了工作空间的边界。各驱动副行程li=lmax-lmin，其大小直接影响操作空间的大小。

2) 从动杆的干涉：设各从动杆截面都是边长为m的正方形，两相邻杆中心线间的最短距离为M，则两杆之间不发生干涉的条件为

M>m。

3) 各转动关节的转角限制。由于各转动关节的转动范围有限，所以关节转角也限制了各支链从动杆的转动幅度：

θmin<θi<θmax

2.1.2 计算分析结果

基于MATLAB R2014a数值计算分析的工作空间，见图6。由图6可求出在动平台姿态角为0度时的最大工作空间面积为39 885 mm2，工作空间最大内切圆半径为100 mm。

2.2 不同姿态角对工作空间的影响

不同姿态角下的工作空间对比如图7所示。由图7可知，当动平台的姿态角为0度时，机构的工作空间最大；在改变动平台姿态角时，工作空间也会随着旋转一定的角度，并且工作空间的面积也会随着减小。

图6 动平台姿态角0°时的工作空间Fig.6 The working space of the moving platform at the attitude angle of 0 degrees

图7 不同姿态角下的工作空间对比图(0°，15°，30°，45°，60°)Fig.7 A work space contrast diagram with different attitude angles(0 degrees, 15 degrees, 30 degrees, 45 degrees, 60 degrees)

3 3-PRR并联机构灵巧度分析

3.1 不同姿态下的条件数的倒数值

3-PRR机构的雅克比矩阵条件数的倒数值越大，机构的运动学性能越好。3-PRR机构雅克比矩阵条件数的倒数值如图8所示。可以看出，工作空间中心处机构的运动学性能比边缘处机构的运动学性能要好。

3.2 不同姿态下的最小奇异值

最小奇异值越大，越有利于动平台的快速响应，也越有利于控制操作的最大速度。动平台在不同姿态下的最小奇异值变化，如图9所示。

图8 不同姿态角时的条件数倒数Fig.8 The reciprocal of the condition number of different attitude angles

由图9可以看出，当动平台姿态角为0°时，机构的最小奇异值较小，不利于动平台的快速响应；当动平台姿态角为15°时，机构的最小奇异值有明显的增大，动平台易于快速响应控制；当动平台姿态角增大到30°、45°时，最小奇异值变化较小，机构的快速响应特性和姿态角为15°时无较大差异。

图9 不同姿态角下的最小奇异值Fig.9 The minimum singular value of different attitude angles

3.3 不同姿态下的可操作性

可操作性的值越大，动平台的工作灵活程度越高。动平台在不同姿态下的可操作性变化图，见图10。

图10 不同姿态角下的可操作性Fig.10 The maneuver ability of different attitude angles

从图10可以看出，当动平台姿态角为0°时，机构的可操作性较小，动平台的灵活程度较低；当动平台姿态角为15°时，机构的可操作性有明显的增大，动平台灵活程度较高；当动平台姿态角增大到30°、45°时，可操作性也随之增大，动平台灵活程度较好。

4 总结

本研究建立了机构的运动学反解和正解数学模型，并对运动学反解进行了实例计算验证，得出特定轨迹下杆长、速度、加速度的变化曲线；根据约束条件，计算出不同姿态下动平台的工作空间，分析了动平台姿态角对工作空间的影响；并推导出速度雅克比矩阵，计算出在不同姿态下雅克比矩阵条件数的倒数值、最小奇异值、可操作性在工作空间分布，分析了机构的灵巧度特性。