多场耦合粘弹性轴向运动板减振分析
张超越,滕英元,方 勃
(沈阳航空航天大学 航空宇航学院,沈阳 110136)
在绝大多数工程振动系统中,振动都被认为是有害的。机械振动会导致轴承磨损过大,紧固件松动,结构性或机构性失效和降低效率等。很多方法可以用来减小传递到被激振结构的振动,理想的方法是设计低噪声机械设备,或者通过加入外部设备,比如动力吸振器来减少振动响应。其中在振源和接受结构之间引入隔振元件的方法是目前最为关注的振动控制方法,即通过改变传递途径的方式达到隔离振动的目的。被动隔振器是一个承载并且消耗能量的元件,它结构简单,不需要外部能量,并具一定经济性优势,因此在很多情况下成为解决工程振动传递问题的首选方案[1]。目前广泛采用的轴向运动结构包括轴向运动弦线、梁、薄膜以及板等模型。从力学角度而言,梁模型和板模型为基本模型,它们不但具有陀螺连续体的共性还具有陀螺连续体的特性。从数学模型角度而言,轴向运动结构属于无穷维陀螺连续系统,陀螺项的存在对动力学分析提出重要的理论要求。轴向运动梁和面内运动板的控方程及其非齐次边界条件都属于时变系统,这给问题的求解带来诸多技术困难。因此,研究轴向运动板的横向振动问题具有深远的科学研究价值。对于轴向移动板块,Ling[2]总结了不同边界条件下轴向运动板的稳定性分析方法。Tang和Cheng[3,6]用多重尺度的方法研究轴向移动板的自由振动,计算了板的非线性固有频率,并研究了轴向加速粘弹性板的稳定性。对于轴向运动粘弹性材料,Yang[4]采用有限差分法研究了轴向运动板的稳定性和非线性振动。Zhou和Wang[5]用微分方法(DQM)研究了粘弹性板的稳定性,分析了厚板厚度对板的散度速度的影响。张也弛[7-9]研究了非线性能量阱的靶能量传递与参数设计及非线性耦合振子间产生靶能量传递的初始条件。陈予恕院士[10]应用非线性能量阱对机翼极限环的抑制研究扩展到含有复杂结构非线性机翼的非定常流中。同年,杨天智和张业伟等人[11-12]利用非线性消振装置对输液管道的振动和受风载作用的轴向运动弦线振动进行了抑制研究,该装置易于工程实现,可靠性高。熊怀[13]等人研究了耦合非线性能量阱的非保守系统的定向能量传递现象,获得了系统能够实现定向能量传递时阻尼必须满足的条件,并给出非线性能量阱具有吸振能力时线性振子阻尼的有效范围。张业伟[14]等人将NES用于抑制热冲击下的轴向运动梁的振动,有很好的抑制效果。本文研究的创新点是板是轴向粘弹性板,在气动热环境下的动力特性与振动抑制,所加的NES对板的横向振动有一定的减振效果。
1 基于NES的多场耦合粘弹性轴向运动板动力学模型
考虑一个轴向移动平板与移动速度V0在x方向上如图1所示,长、宽、厚分别为a,b和h的板。周围的气流是不可压缩的、无粘且无旋,质量密度为ρ,流速为Uf。板的应变-位移关系可以表示为
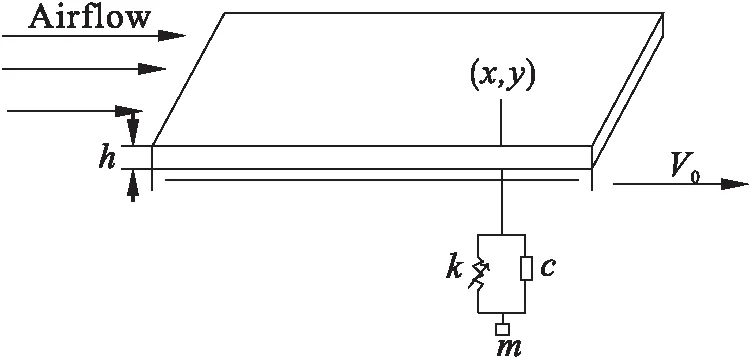
图1 具有NES轴向板示意图
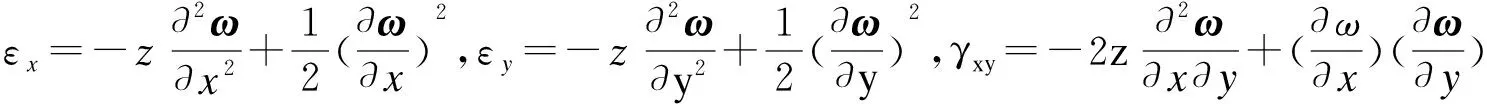
(1)
ω=ω(x,y,t)是板的横向位移,εx,εy,γxy是线应变和切应变。板的本构方程可表示为
(2)
σx,σy和τxy是应力分量,E是弹性模量,μ是泊松比,η是粘弹性系数。板的应变能可表示为
(3)
板的总动能,包括与横向振动和纵向运动有关的动能,可表示为
(4)
T是总动能,板的质量密度是ρ。
外力做功可表示为
(5)
Δp是轴向运动板与周围气流之间的相对运动所产生的气动力,F(x0,y0)是作用于板上(x0,y0)的外力,热荷载FT表示为[15]
(6)
α是热膨胀系数,ΔT是温度的变化。
板的简支边界条件可表示为
(7)
根据假设模态法(AMM),板的横向位移可写为
W(x,y)Tq(t)
(8)
其中M和N是x,y方向的模量而上标表示矩阵的转置。轴向运动板的周围气流是用线性势流理论模拟的理想流动。根据参考文献[16]中应用的方法,我们可以得到以下微扰气动力的表达式
Δp=ρ
(9)
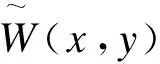
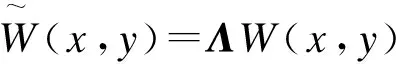
(10)
这里Λ是一个对角矩阵。把公式(8)~(10)代入公式(3)~(5),势能,动能和外力做功表示为
(11)
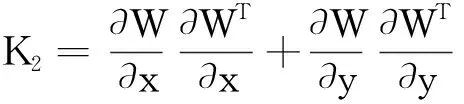
Mf=ρ
(12)
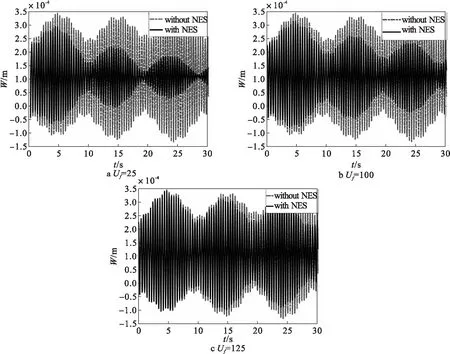
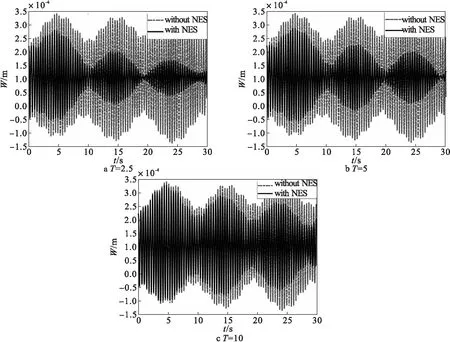
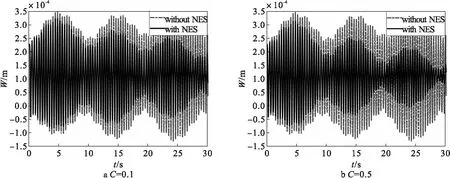
A={(x,y)|0 在式(12)中,下标f的矩阵与流动气流有关,下标V的矩阵与运动速度有关,下标T的矩阵与温度变化有关。 由哈密顿原理 (13) δ表示变分符号,t1和t2是积分时间限制。将势能、动能和外界功代入式(12),可得到轴向运动板的运动方程如下 (14) (15) 这里M,C,K分别是质量、阻尼、刚度矩阵,下标f的矩阵表示气动力项,下标T的矩阵表示热效应项。R(q)是由几何非线性引起的立方非线性项。公式(14)是在气动热环境下轴向运动粘弹性板的动力学模型。它反应了轴向运动板与轴向运动速度、气动力、热荷载的关系。 忽略公式(14)中的立方非线性项和外激励力项,可以得到线性系统 (16) (17) 仍以四边简支板为研究对象,其边界条件和模态函数如上述所示。则可得到系统的运动微分方程组 (18) 本文板的结构与材料特性:ρ=7 600 kg/m3,E=70 GPa,μ=0.3,a=1 m,b=0.8 m,h=0.003 m。板的热膨胀系数α=4×10-6(1/℃),周围气流的质量密度是1.29 kg/m3。NES的质量m=1 kg,c=0.1,k=100 N/m。 在区间Uf∈[25,125]m/s范围内,其它参数分别为m=1 kg,k=100 N/m,c=0.1,T=2.5℃,研究空气流速对板振动的影响。图2为不同空气速度对板振动的影响。由图2可以看出,在所研究的区间内,板的横向振动随空气流速的增大而增大。 在区间T∈[2.5,10]℃,其它参数分别为Uf=25 m/s,m=1 kg,k=100 N/m,c=0.1,研究外界温度对板振动的影响。图3为不同外界温度对振动的影响。由图3可以看出,板的横向振动随温度变化的增大而增大。 图2 不同空气速度对板振动的影响 在区间m∈[0.5,1.5]kg范围内,其它参数分别为T=2.5 ℃,Uf=25 m/s,k=100 N/m,c=0.1,研究NES质量对板振动的影响。图4为系统的位移时间响应随NES质量的影响。由图4可以看出,在所研究的区间内,板的横向振动随NES质量的增大而减小。 图3 不同外界温度对板振动的影响 在区间k∈[100,900]N/m范围内,其它参数分别为T=2.5 ℃,Uf=25 m/s,m=1 kg,c=0.1,研究NES刚度系数对板振动的影响。图5为系统的位移时间响应随NES刚度系数变化的影响。由图可以看出,在所研究的区间内,板的横向振动随NES刚度的增大而增大。 图5 不同NES刚度系数对板振动的影响 在区间c∈[0.1,1]范围内,其它参数分别为T=2.5 ℃,Uf=25 m/s,m=1 kg,k=100 N/m,研究NES阻尼系数对板振动的影响。图6为系统的位移时间响应随NES阻尼系数变化的影响。可以看出,在所研究的区间内,板的横向振动随NES阻尼系数的增大而减小。 图6 不同NES阻尼系数对板振动的影响 本文基于von Karman非线性板理论和线性势流理论,根据哈密顿原理建立了气动热环境下具有NES的粘弹性板动力学模型。通过数值仿真,得到位移时间响应曲线,并研究了外界温度,空气速度,NES质量、刚度、阻尼对轴向运动板振动的影响。研究结果表明,在给定参数范围内,NES对轴向运动板的振动可以达到很好的振动抑制效果。虽然本文的研究偏重理论基础,但由于NES具有简单容易应用的特性,所以本文的研究对于航天工程中结构上敏感部件的振动抑制具有实际的指导意义。

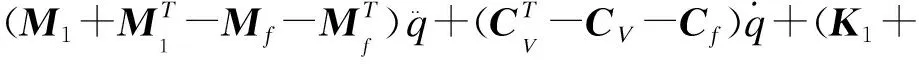

2 多场耦合粘弹性轴向运动板仿真分析及减振分析
2.1 空气速度对板振动的影响
2.2 外界温度对板振动的影响
2.3 NES质量对板振动的影响
2.4 NES刚度系数对板振动的影响

2.5 NES阻尼系数对板振动的影响

3 结论

