利用地面景象信息辅助的无人机自主定位技术

徐喜梅，黄大庆，徐 诚

(1.南京航空航天大学电子信息工程学院，南京 210016;2.南京航空航天大学中小型无人机先进技术工信部重点实验室，南京 210016)

0 引言

无人机 (Unmanned Aerial Vehicle)是一种无线遥控的无人驾驶飞机。最初无人机的诞生是用于军事上，随着信息技术的高速发展以及高新技术在武器装备的应用，以及我国低空空域对民用的开放，其使用范围已拓宽到军事、民用和科学研究三大领域，无人机的应用将是一个巨大的潜在市场［1］。无论是在军事、民用、还是科学研究领域，无人机在执行任务时首先要解决的问题就是确定自身在工作环境中的准确位置，因此无人机自主定位是无人机执行任务的基础和关键。

传统的无人机自主定位技术使用最广泛的是GPS导航和惯性 (IMU)导航，其可以提供精确的位置和姿态信息，而卫星信号易受干扰、技术敏感，以及惯性测量单元的成本较高，且测量结果会随时间漂移，存在误差累积的问题，不适合进行长时间、远距离的定位应用。近年来，视觉传感器在无人机的自主定位技术中应用越来越广泛，基于图像匹配的无人机自主定位技术已成为研究热点，其中利用图像匹配导航技术确定无人机位姿参数的研究，国外开始的比较早，最初其研究主要是采用光学传感器，结合相机成像原理以及计算机视觉理论推导出无人机相对位置信息［2］，后期又有利用相对位置和绝对位置估计复合定位算法，该方法虽然计算精度比较高而且克服了一些地理位置的不足，但其对设备性能要求很高，且计算量非常大。另外澳大利亚Monash University提出了一种结合GPS的图像导航的无人机自主定位方式［3］。在国内此方向的研究起步比较晚，大多是在算法上的研究工作，包括基于地形辅助的图像导航研究，此系统研究比较成熟，但其一般适用于地形起伏比较大的地方［4］，利用影像匹配和摄影测量法实现无人机自主定位导航［5］，其前提是要求一幅图像上必须有3个以上的同名点已知。利用雷达实现无人机自主定位［6］，然而该方法对无人机飞行路径的地貌特征有苛刻的要求，增加了计算量，且实时性较差。

本文在研究分析了上述各种方法优缺点的基础上，设计了一种利用地面景象信息辅助的无人机自主定位算法，此算法能够在误差允许范围内，解决无人机的GPS信号接收机丧失定位功能时，无法获取无人机自身的位置信息的问题，具有较大的实用价值，且简单易于实现。

1 无人机自主定位算法

本文提出的利用地面景象信息辅助的无人机自主定位算法，首先假设在平坦区域内，利用景象匹配导航技术，将无人机拍摄的实时航拍图，与预先储存在无人机计算机内的地面景象的数字化地形图进行图像匹配，从匹配结果中获取数字化地形图上的一个同名像点D和此点对应在实时航拍图像上的点D'，利用数字化地形图所提供的地理位置数据，获取此同名像点D的大地坐标信息，最后结合机载光电测量系统的坐标转换过程，推导出无人机的大地坐标信息，实现无人机的自主定位。基于地面景象辅助的无人机自主定位的模型如图1所示。其中地面景象的数字化地形图的获取可以通过大地测量、航空摄影、卫星摄影或是已有的地形图等方法将地形数据 (主要是地形位置和高度数据)制成数字化地形图［7］。最后利用蒙特卡罗思想设计无人机自主定位误差模型，并进行仿真试验及误差分析。本研究在无人机GPS定位系统失效的情况下，充分利用无人机飞行区域的地面景象数字化地形图的地理位置数据，以及无人机位置与地面上同名像点位置之间的几何关系，再结合机载光电测量系统的坐标转换过程，实现无人机的自主定位过程，此自主定位算法富有一定创新性，且简单易于实现。

1.1 无人机自主定位辅助坐标系

利用地面景象辅助的单点定位算法实现无人机的自主定位，在此过程中需要定义以下几个辅助坐标系:

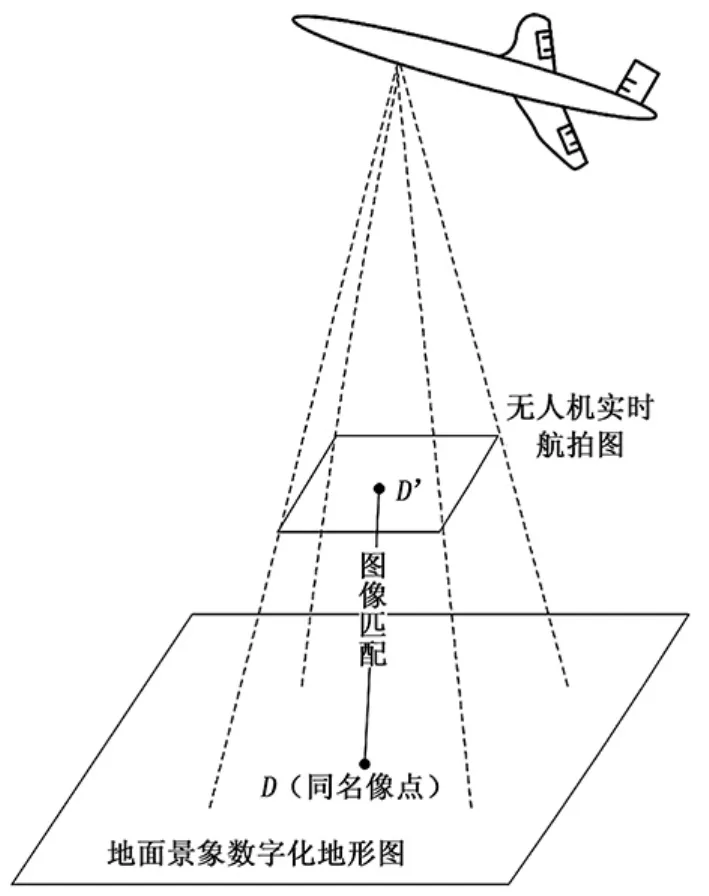
图1 基于地面景象辅助的无人机自主定位模型

1)摄像机坐标系T(Ot－XtYtZt):原点在摄像机光轴与横轴的交点上，Zt轴为摄像机光轴指向目标，光轴指向角以方位角α和高低角β表示，其中方位角α为绕方位轴Xt的旋转角度，高低角β为绕俯仰轴Yt的旋转角度。

2)载机坐标系A(Oa－XaYaZa):原点是某一时刻载机质心所处的位置，Xa轴由机腹指向机背，Ya轴代表无人机横轴，Za轴代表无人机纵轴。设ψas，θas，φas为三轴姿态角，分别绕Xa(偏航)，Ya(俯仰)，Za(横滚)的旋转。

3)地理坐标系S(Os－XsYsZs):Zs指向正北方向，Xs指向天顶，Ys与Zs、Xs构成右手坐标系，指向西为正。本文定义两个地理坐标系，首先地理坐标系Su定义为其原点是某一时刻无人机质心所处的位置(Bu，Lu，Hu)。地理坐标系Sd定义为以地面对应同名像点所处的位置(Bd，Ld，Hd)为原点。两坐标系的X，Y，Z三轴指向相同且互相平行。

NEU坐标系N(ON－XNYNZN)［8］:其原点为地面对应同名像点所处的位置(Bd，Ld，Hd)，XN轴正方向指向正北，YN轴正方向指向正东，ZN轴与XN轴YN轴构成右手坐标系，指向天顶为正。

4)大地直角坐标系G(Og－XgYgZg)，大地坐标系C(Oc－ XcYcZc)［9］。

1.2 无人机自主定位原理

无人机的自主定位流程图如图2所示，首先利用景像匹配导航技术获取地面景象的数字化地形图上的一个同名像点D，以及此点的大地坐标值。利用无人机的激光测距仪获取无人机与地面上对应同名像点D的距离R。定义此同名像点D在摄像机坐标系下的坐标为(0，0，R)，利用各个坐标系间的转换关系可以得到点D在地理坐标系Su中的坐标值，利用两地理坐标系Su和Sd之间的空间几何关系如图3所示，点D在Su地理坐标系V，VI，VII，VIII四个象限的情况相同，因此本文只讨论同名点D位于VIII卦限的情况。将点D在地理坐标系Su中的坐标值X，Y，Z均加反向符号，即可获得无人机在地理坐标系Sd中的坐标值，继而求出无人机在大地直角坐标系中的坐标值 (Xu，Yu，Zu)，最后利用公式 (8)求出无人机大地坐标系(Bu，Lu，Hu)。

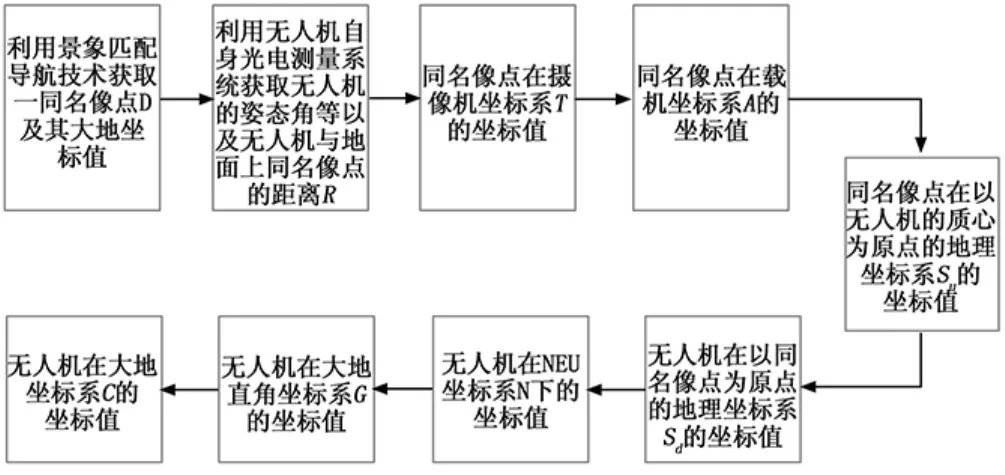
图2 无人机自主定位流程图

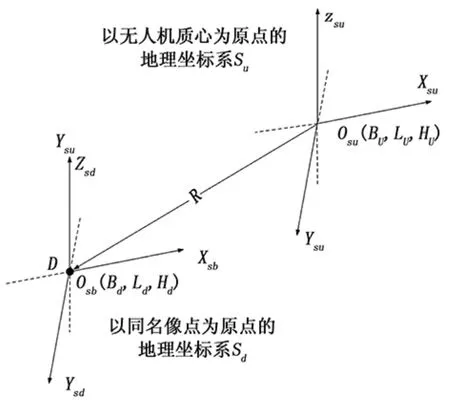
图3 地理坐标系Su和Sd之间的空间几何关系

1.3 无人机自主定位计算过程

无人机自主定位过程，即已知同名点D的大地坐标(Bd，Ld，Hd)，无人机姿态角 ψas，θas，φas，摄像机的方位角α、高低角β，以及无人机与地面同名像点D之间的距离R，求解无人机大地坐标(Bu，Lu，Hu)的过程。

具体计算过程如下:

1)已知同名像点D在摄像机坐标系中的坐标T=(0，0，R)，将T代入公式 (1)可得无人机在NEU坐标系中的坐标值N=(n，e，u)。

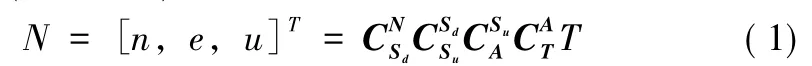
2)NEU坐标系N到大地直角坐标系G的转换关系:

已知无人机在 NEU坐标系N下的坐标值为(n，e，u)，NEU坐标系原点ON的大地坐标为(Bd，Ld，Hd)，大地坐标系C(Oc－XcYcZc)到大地直角坐标系G(Og－XgYgZg)之间的转换关系如式 (6)所示。则NEU坐标系N(n，e，u)到大地直角坐标系G(Og－XgYgZg)的变换如式 (7)所示。

y0，z0为NEU坐标系原点ON的大地坐标(Bd，Ld，Hd)在大地直角坐标系G中的坐标表示。

3)大地直角坐标系G转换到大地坐标系C有两种方法，迭代法和直接法［10］，本文采用直接法，如公式 (8)所示。

最后由无人机在大地直角坐标系下的坐标值(Xu，Yu，Zu)带入公式 (8)求得无人机在大地坐标系下的坐标值(Bu，Lu，Hu)。

2 无人机自主定位性能分析

为了对利用地面景象信息辅助的单点定位算法，实现无人机自主定位的性能进行分析，本文采用蒙特卡罗统计实验的方法，对本文无人机自主定位的误差进行仿真试验。由于定位方程会涉及到大量的矩阵相乘，其运算和结果比较繁琐因此本文采用MATLAB程序进行仿真。

2.1 蒙特卡罗法应用于无人机自主定位的误差分析

蒙特卡罗法也称统计试验法或随机模拟法，它是通过随机变量的统计或随机模拟，求解数学、物理和工程技术问题近似解的数值方法［11］。本文利用蒙特卡罗方法，模拟一套定位误差源的样本值而且各个样本值相互独立，随着样本数量的增加，大量的模拟结果就与实际结果非常接近，因此充分考虑样本的数量以及计算时间，使得计算结果具有很高的置信度［12］。

无人机自主定位误差模型用蒙特卡罗法可以表示为:

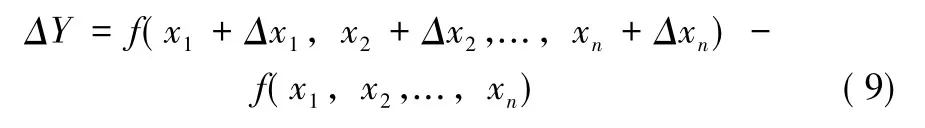
其中:x1为坐标转换中各参数的测量值，Δxi为各参数测量误差;f为定位计算过程。

基于地面景象辅助的无人机自主定位的计算方程可以简单表示为:

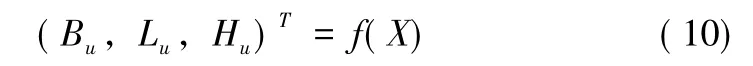
则定位误差模型:

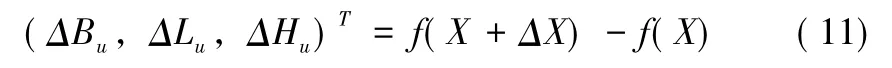
其中:Bu，Lu，Hu为无人机在大地坐标系下的坐标值，ΔBu，ΔLu，ΔHu为无人机定位误差，X，ΔX分别表示转换中各参数的测量值和测量误差。这些参数包括:无人机与地面上同名点之间的距离，无人机姿态角，摄像机的方位角、高低角，同名点大地坐标;

参数的误差模型:

由式 (11)可知定位误差与多种因素有关，包括各个参数的测量值及其误差，由概率论知识可知这些参数的误差大都服从正态分布。因此假设定位计算的参数误差ΔX服从均值为0，均方差为σΔX的正态分布即:

在计算机仿真中，利用MATLAB提供的randn()函数，产生服从标准正态分布的随机数序列X'。经过转换ΔX=σΔXX'就可以得到正态分布的随机数ΔX～N(0，σΔX)。

2.2 定位仿真程序设计

首先根据无人机实际飞行数据记录各个量的名义值，参数的误差值 (均来源于平台各个部件的说明书)，将仿真计算过程中所用到的参数的名义值，误差值列于表1中。本文根据基于地面景象辅助的无人机自主定位方程，以及用蒙特卡罗法设计的定位误差分析模型编写误差仿真的MATLAB程序，其详细计算步骤如下所示:

1)初始化程序;

2)首先按照表1输入各参数的真实值，设定所有参数误差为零，求得无误差情况下的定位结果(Bu，Lu，Hu)，记录数据。

3)利用randn()函数，生成服从正态分布的各个参数的随机数X'，设定随机序列长度为10 000;

4) 根据随机误差量Δ Xi=σΔXXi'，其中σΔXi是表1中的误差值。用蒙特卡罗法计算加入误差后的定位结果(Bi，Li，Hi);

5) 计算 (ΔBi，ΔLi，ΔHi)=(Bi，Li，Hi) － (B，L，H);

6) 统计(ΔBi，ΔLi，ΔHi)的标准差并输出结果。

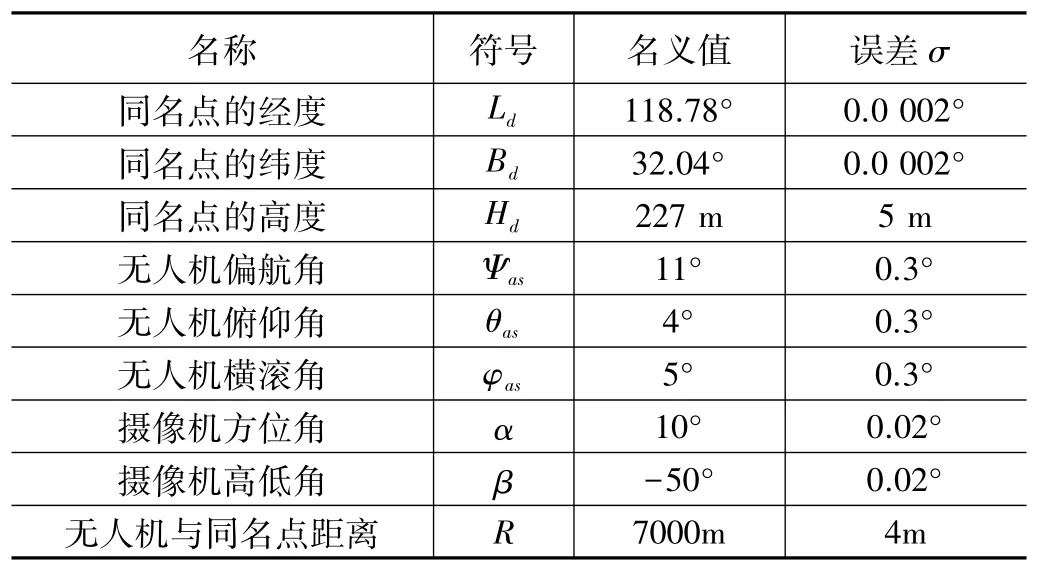
表1 无人机自主定位仿真数据

2.3 仿真结果和误差分析

利用上述的仿真步骤建立的定位模型和误差仿真模型结合表1仿真数据进行仿真试验，最终得到无人机的经纬度和大地高的误差分布，以及无人机自主定位结果的空间分布，试验结果如图4所示，其中由图 (a)、图 (b)、图(c)可以看出，无人机的经纬度和大地高的误差分布皆服从μ=0的正态分布。无人机自主定位的结果中心占的比例最大，呈中心分布形状符合正态分布，采用表1数据计算无人机自主定位误差，并对试验结果经过统计求均值可以得到，经度误差0.000343°，纬度误差为0.000259°，高程误差21.1 m，换算为空间误差为20.9 m。

利用本文的无人机自主定位算法和表1的数据，结合对定位误差的实验结果的分析，最终会得到一个定位结果及误差，如表2所示。

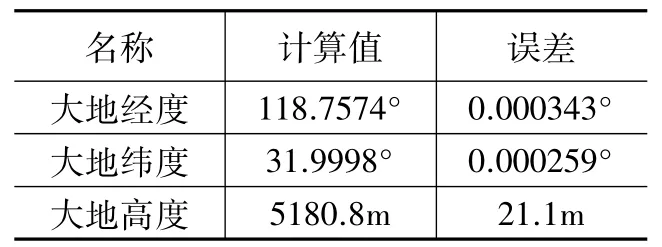
表2 无人机定位结果

3 总结

本文提出了一种利用地面景象信息辅助的单点定位算法，实现无人机的自主定位。本算法首先利用景象匹配导航技术，获取无人机拍摄区域内对应地面上的一个同名像点，结合地面景象的数字化地形图提供的地理位置信息，获取此同名像点的位置坐标信息，利用同名像点位置与无人机位置的几何关系定义多种辅助坐标系，通过机载光电测量系统的坐标转换过程推导出基于地面景象辅助的单点定位方程，最终实现无人机的自主定位过程。最后本文利用蒙特卡罗思想对无人机自主定位误差进行仿真试验。经试验证明，此算法在误差允许范围内能够实现无人机的自主定位过程，可以有效的解决无人机在室内、恶劣环境中或是受敌方电子干扰时，GPS信号接收机丧失自主定位功能的问题，本研究具有较高的实用性和可行性。

图4 试验仿真结果