基于灰关联度赋权的道路交通安全模糊评价

张文晰

(西华大学汽车与交通学院，四川 成都 610039)

随着道路交通的发展，交通事故频发，我国交通安全的形势极其严峻，交通安全问题已经成为全社会共同关注的焦点；因此，针对道路交通安全事故的预防对策进行研究显得尤为重要和迫切[1]。建立科学的评价指标体系，采用适当的方法评测道路交通安全变化趋势，了解道路交通安全态势，对制定符合实际的交通安全管理法规有着重要的指引作用[2]。

1 评价方法与赋权方式

目前，交通安全评价的主要方法有回归分析评价、贝叶斯方程、遗传模糊 TOPSIS 、模糊综合评价法等[3]，其中模糊综合评价法是交通安全评价中应用最多的主观评价方法。模糊综合评价方法是对受多种因素影响的事物，做出全面评价的一种有效方法[4]，它运用模糊数学的原理，由层次分析法AHP赋权，按模糊变换和最大隶属度原则，考虑与被评价事物相关的各个因素影响而进行的一种主观性的综合评价方法。这种主观性在一定程度上会影响评价的有效性；因此，如果能在此基础上进行改进，主观和客观相结合，评价结果会更有说服力。

为了改进模糊综合评价法的主观性，最为有效的方法是直接改变评价方式的赋权方式。采用客观的赋权方式代替模糊综合评价法中AHP的主观赋权方式，能形成更为有效的主客观相结合的评价方法。客观赋权法是根据指标间的相关关系及指标值的变异程度来确定权重，主要方法包括主成分分析法、因子分析法、变异系数法和复相关系数法等[2]。范东凯等[5]将主成分分析法引入城市道路交通安全评价的赋权，余思勤等[6]将因子分析法用于交通运输业发展的总体评价，有研究将因子分析法用于道路交通安全评价与决策研究[7]。

现将改进后的灰关联赋权方式代替层次分析赋权用于道路安全模糊评价。灰理论是由邓聚龙在20世纪70年代末、80年代初提出的，对少信息和少数据系统处理的理论[8]。灰色关联分析理论是灰理论中重要的理论之一，是对两个系统之间的因素，其随时间或不同对象而变化的关联性大小的度量。改进后的灰关联赋权是通过收集各指标的少量数值信息，计算在某个系统中，其他指标对其中选定的一个指标的关联程度，通过关联度的改进来确定各指标的权重的一种赋权方式。灰关联理论的不完全信息和数据特性，在收集道路安全信息和数据困难的情况下更具优势，既能客观地赋权，又能利用较少数据准确地评价道路交通安全，相比其他的客观赋权方式，评价结果更具有科学性。

2 灰关联赋权方式下的模糊评价方法

灰关联赋权方式下交通安全模糊评价过程如下：首先建立评价指标；然后通过灰关联赋权方式取各评价指标的权重；随后调查交通使用者对各指标赋予的安全等级，并建立模糊评价矩阵；最后通过权重与评价的乘积取得评价的等级值，根据模糊理论的隶属度原则，选取评价值最大的等级作为被评价对像的最终等级[9]。

2.1 指标体系的建立

关于道路交通安全评价指标的选择：有研究从宏观层面出发，以人机环以及所属的指标作为评价标准[10]；也有部分研究从道路的硬件和软件角度评价安全性；部分研究采用机动车、自行车和行人导致的事故死亡率作为评价标准[11]。事故导致的死亡率有限，多数交通事故的发生并不会导致死亡，在此基础上，可采用事故率作为评价标准。

本文在选取评价指标时，抛开人机环的角度，从引发交通事故的主体角度考虑。由于各种类型交通事故是直接反应了交通运行过程中人机环带来的安全性的最终体现，那么选择当交通事故发生时，把机动车、非机动车和行人作为主要责任者，引发并产生的交通事故率作为城市道路安全评价的主要指标是可行的。表1中，C1至C9代表机动车、非机动车和行人引发的交通事故率，它们作为评价道路交通安全的指标。

表1 道路安全评价指标

2.2 改进的灰关联赋权方法

根据表1，机动车所包含的各类型车辆，非机动车所包含的自行车和电动自行车，以及行人共同组成了道路交通安全的主要参与者。以主要参与者为主要责任引起的各类型交通事故率作为评估指标，权衡各指标对道路交通安全的影响能力，采用灰关联对指标的影响能力进行赋权[8，12-15]。

根据原始数据建立矩阵

(1)

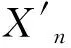
对式(1)进行无量纲化，数据序列形成以下矩阵：

(X1,X2，…,Xn)=

(2)

把规范化的序列X1作为比较序列X0，每个序列和X0进行比较，可获得以下矩阵：

(X0,X1，…,Xn)=

(3)

根据式(3)，第k行中的第i个评价指标与参考值的关联系数ζi(k)是比较数列与参考数列在第i个指标的相对差值，差值的大小可作为衡量两数列关联程度的尺度，即ζi(k)越大，两个数列在第i个指标上的关联程度越大。计算该关联系数的公式为

ζi(k)=

(4)

式中ρ为分辨系数，0<ρ<1，一般取0.5[8]。

最终，取每列的关联系数的平均值作为各列与参考列之间的关联度，公式如下：

(5)

实际所得的各个关联度值反映了第i个实际因素值与参考值的关联程度，那么各关联度占全部关联度之和的比重，即为各因素的权重；因此，灰关联度下的权重为

(6)

2.3 灰关联赋权下的模糊评价

当计算获得各指标的权重后，由指标集合U和评价等级V构建模糊评价矩阵R。通过抽样调查，交通使用者根据自身对道路安全度的主观感受对各指标的安全性进行选择，将每个指标各等级选择人数占总人数的比例作为R的具体值，最后进行模糊矩阵和权重的评价运算[9]。

B=w∘R=(bj)，j=1,2,…,m。

(7)

对式(7)进行归一化后，取最大值

bmax=max{b1,b2,…,bm}=bj。

(8)

根据模糊原理的隶属度原则，选取数值最大的等级作为该系统的最终评价等级。

3 评价方式的实例分析

采集2016年某城市某区域5条道路的数据，区域内以C1至C9交通主体引发并负主要责任的事故率如表2所示。

表2 城市道路事故率 %

由表2建立矩阵并进行无量纲化，确定参考数列x0=x1，可获得下列矩阵：

通过计算，获得：

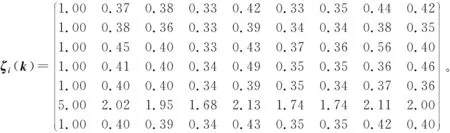
各因素与参考序列的关联度

可确定C1至C9各权重如表3所示。

取得指标集合U=(C1，C2，C3，C4，C5，C6，C7，C8，C9)。

表3 指标权重值

评语的模糊集合V=(非常安全，安全， 一般，不安全，极度不安全)。

采取抽样调查方式，对该区域交通使用者进行调查，获得的数据如表4所示。

表4 交通使用者调查表

由表2可得到模糊评价矩阵

代入权重值，计算得到

B=w∘R=(0.14 0.11 0.22 0.22 0.17)。

通过归一化处理后，可得表5。

表5 道路安全评价

根据表5，评价值中最大值为0.255 8。由模糊评价隶属度原则可知，此城市道路交通的安全水平处于一般和不安全状态；由此可得出结论，该城市区域道路交通安全性较差，需要相关管理部门加强交通安全管理。

通过上述实例可以看出，灰关联赋权是利用现有的已发生的少量信息和数据，通过计算各指标对目标的贡献度，获取各指标权重。相比层次分析法赋权是由专家的经验决定而言，改进后的灰关联赋权更为客观有效。同时，赋权方式的客观化与评价方式的主观化结合在一起，避免了单纯的主观和单纯的客观带来的弊端，更加科学合理。

4 结论

本文针对道路安全模糊评价方式的主观性，对模糊综合评价的赋权方式进行了改进。由于灰理论具有少信息、少数据的特性，采用了客观的灰关联赋权方式代替主观的AHP赋权。同时，利用交通参与者引发的事故率，建立城市交通安全系统的评价指标体系，最终建立了基于灰关联赋权方式下的城市道路安全模糊评价方法，实现了评价方法的主客观相结合。本文使用该方法，对某城市区域的交通现状进行了安全评价分析，通过计算，得出了该城市区域道路安全状况不安全、不理想的评价结果。