基于小波算法的风电储能装置优化控制

程 琳，都小利，王月兵，钱 文

(1.国网安徽省电力公司培训中心， 安徽 合肥 230022； 2.安徽电气工程职业技术学院， 安徽 合肥 230051；3.国网安徽省电力公司安庆供电公司， 安徽 安庆 246000； 4.国网安徽省电力公司亳州供电公司， 安徽 亳州 236800)

风电以其自身的实用、环保等特性，成为目前可再生新能源利用中最具大规模开发条件、技术最成熟、发展前景最为看好的发电方式。表1为不同能源发电方式的经济成本。可知，作为新能源之一的风电具有资源巨大、易开发、低碳环保等优点。然而，风能大小和方向常具有随机性、间接性等特点，这使得风力发电所产生的有功功率常存在不确定性，难以预测。如果风力发电系统构成孤网将使得孤网内重要负荷工作不稳定；如果风力发电系统与大电网相连接，这将影响大电网的频率稳定[1]。根据我国地理条件，具有丰富风力资源的地区大都位于丘陵、山区。这些地方的电网基础建设相对落后，对电网的稳定性保护也较为薄弱,因此如果将风力发电系统直接接入传统大电网，会影响整个大电网工作的稳定性，甚至会带来大电网的瘫痪[2]。与此同时，风电消纳能力受到极大限制，高比例的弃风现象普遍存在，会造成资源浪费和风电企业的经济损失[3-4]。

表1 不同能源发电方式的经济成本

文献[5-6]指出风力发电系统与大电网相连时，电网将消纳风力发电系统所产生的电能。如果风力发电产生的电能超出电网消纳能力，电网中已有的发电机的机械功率会发生变化，发电机输出功率也相应发生变化。为补偿风力发电所产生的波动输出功率，文献[7-8]将蓄电池并接至大电网系统中。文献[9-11]采用长时间序列算法、NSGA2算法等对风速进行预测，希望通过预测风速能估算出风力发电系统的输出功率变化，但对风的变换进行精准预测是非常困难的。自然界气候的变换常难于预测，因此提高风力发电机输出电压和频率质量的方法是在发电系统中增加储能设备，作为能源调节器。为此，本文设计了基于小波算法的分布式储能装置控制模型，以提高风力发电并网后的电能质量，并在建模的时候，将风力发电所需储能的容量与建设成本等因素综合考虑，从而达到提高风力发电效率的目的。

1 储能装置及接入

当风力充足而用电量较少时储能装置起到电能储存作用；当风力不充足，用电量较大时，储能设备将释放电能，从而维持系统中重要负荷的稳定工作。在运用风能大规模发电时，由其本身特性的原因，必须结合合适的储能装置来平滑输出功率达到提高电能质量的目的。表2列出了储能方式的各项指标。可以看出，不同的储能方式各有优势，适用于不同的情况。

表2 储能技术特性比较

目前对于储能设备与电网的连接方式有2种：集中式和分布式。集中式是在电网中统一安装较大容量的储能装置，这样的接入方式虽然减少了经济成本和维护人员工作量，但当风力发电产生的有功有较大波动时，储能系统的响应较慢，甚至可能会失效，这对电网及负荷都有严重的危害。在分布式储能方式中，每台风力发电机都需要配有一个小容量的储能设备，进行输出有功率调节。目前在工业上广泛应用分布式储能技术。综合考虑这些因素,笔者采用分布式储能方式，并选用超级电容储能的方式。当风能过剩时，将多余的能量经直流侧传至电容器吸收并存储；当风能不足时，则反方向将电容器中的能量经由支流母线传输至电网，以平衡所需。

2 分布式储能控制模型设计

在双馈式风力发电机中，在转子侧变流器和网侧变流器之间的直流母线上并接超级电容储能装置，具体结构如图1所示。

为讨论分布式储能装置控制模型工作原理，给出风电储能装置优化控制模型结构图，如图2所示。

图2中Pref是风力发电机的参考输出功率值,P是风力发电机的输出测量值。通过将设定参考阈值与测量值比较，经过功率/电流调节器得到给定电流值I*,再与测量电流值比较,经过功率/电流调节器产生导通占空比，然后与设定的参考三角波比较，得到开关脉冲信号,去触发g1、g2,实现双向变流器的功率控制，从而通过对超级电容器组充、放电控制，实现电容器组内部功率调节。

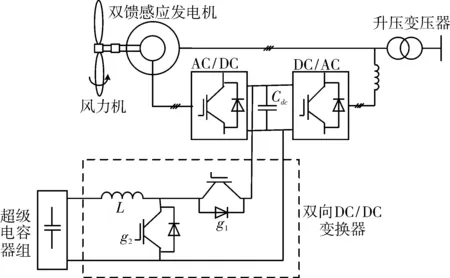
图1 双馈式风力发电机直流侧并联电容器组

图2 控制模型结构图

3 基于小波理论的功率分配判决

小波变换算法相比于FFT变换算法，在时域和频域都具有不同的分辨率，是一种多分辨分析方法。小波时频原子φr(t)可以表示为

(1)

(2)

小波基函数具有尺度因子a和时间平移因子b2个参数。当a增大时，基函数ψa,b(t)的时间窗口也逐渐增大，而频率窗口则逐渐减小。由小波变换的定义，信号f(t)的小波变换WTf(a,b)是a,b的函数，母小波可以是实函数，也可以是复函数。小波算法对原始风电有功功率信号P(t)进行分解，P(t)是实信号，ψ(t)也是实函数，则小波变换得到的结果也是实函数。假定所要分析的函数是任意函数f(t)，Dj+1P(t)表示为在分辨率j和j+1下对P(t)逼近的细节差异，称Dj+1f(t)是在分辨率j+1下的细节函数，dj+1,k是其离散细节，其中：

(3)

(4)

式(3)和式(4)表明，经j-1尺度空间的尺度系数和抽头长度为2k的h(k)滤波器和g(k)滤波器的加权求和可以得到j尺度空间的尺度系数和小波系数。第j级小波分解对应的矩阵2J-j+1×2J-j+1(J为分解层数)为

(5)

小波分解的矩阵表达式为

(6)

因此，小波滤波器h(k)和尺度滤波器g(k)将信号分解为低频分量和高频分量。利用小波算法，首先将在线监测的风力发电输出有功信号经过小波分解，得到相应的高频分量信号与低频分量信号。高频分量信号由于变换速度快，通常给电网带来扰动，破坏电网稳定性；低频分量信号中频率变换较慢，可以作为在线监测的并网功率值，如果过低则会使系统中重要负荷不能工作：因此将小波变换后高频分量信号进行吸收，这样不仅可以平滑功率曲线，同时还可以减小储能电容容量，降低储能系统成本。低频分量信号分别与系统设定阈值比较，从而控制超级电容储能器吸收或补偿的工作状态，达到对电网稳定性进行调节的目的。

4 功率平滑控制

由于风电场输出的功率变换可以被看成是平稳随机过程，因此，在小波算法数据处理之后，在低频分量信号中应用MUSIC(multiple signal classification )谱估计算法，建立非平稳随机时变功率谱，通过比较输出功率与设定阈值之间关系，对超级电容器组充、放电控制，实现电容器组内部功率调节。算法原理框图如图3所示。

图3 功率平滑算法框图

MUSIC算法是基于矩阵特征分解的一种功率密度估计。它将相关数据矩阵中的信息分配到信号子空间，在包含的J个频率中通过MUSIC算法得到功率密度，并进行算术平均。因此，在算术平均意义下的功率密度为

(7)

式中：(·)H表示共轭转置；Us为信号子空间；a(fj)为频率fj处对应的小波分解特征向量。子带频率为fj，在fj处对应的信号X的协方差矩阵表达式为

R(fj)=E[XXH]=UΣUH。

(8)

式中：U为特征矢量矩阵，Σ是由特征值组成的对角阵，其中特征值关系为

λ1≥λ2≥…≥λp。

(9)

λi(i=1,2,…,p)特征值对应的特征向量构成有用信号的子空间Us=[e1,e2,…,ep]，p是子空间维数。通过计算在频率fj的信号自相关矩阵，并进行特征分解，得到其特征值Us。将特征向量a(fj)与Us代入式(7)计算MUSIC功率密度，找出功率密度中p个峰值，并进行算术平均，从而求得超级电容器组内部功率调节值，并与阈值比较，实现对电网功率的平滑控制。

5 仿真分析

为研究储能系统对风电输出功率平滑效果，建立如图4所示的仿真原理图。

图4 仿真原理结构图

图4中，双馈风电场出口电压为690 V,经过变压器接到10 kV电网，再经过传输线路接到220 kV的无穷大系统。超级电容选择接在风电场的出口处，经过变流器和变压器后并入10 kV电网。仿真模型的风电场容量为12 MW,根据我国风电并网标准，每分钟风电场的有功功率变化率不超过装机容量的20%，即风电场的有功功率变换率不超过2.4 MW/min。取时间常数T=9 000 s，如图5所示。

图5 风力发电输出功率

对图5进行不同层次的小波分解，得到图6。本文选择 db6 小波进行数据分解。从图6可以看出，小波分解层数越多，输出功率曲线越平滑，越容易将其分解为高频分量信号和低频分量信号，从而判断电容器充放电状态。

图6 小波分解下的输出功率

电容器容量是指在一段时间内所得到的电容板的充、放电量。本文将频域信号转换到时域，可以根据小波分解后的功率信号计算相应的储能容量。储能容量计算公式为

(10)

式中：E为电容器组容量；P0(t)为时域风力发电系统输出功率，其值为在线监测风力发电输出功率与设定的功率阈值之差。由图7可知，风力发电输出功率中波动部分被电路中的超级电容器组平滑了。

在上述仿真条件下分别采用一阶低通滤波与MUSIC算法、小波算法与MUSIC算法联合的功率调节方法进行比较，验证所提出算法的优越性。仿真结果如图8所示。

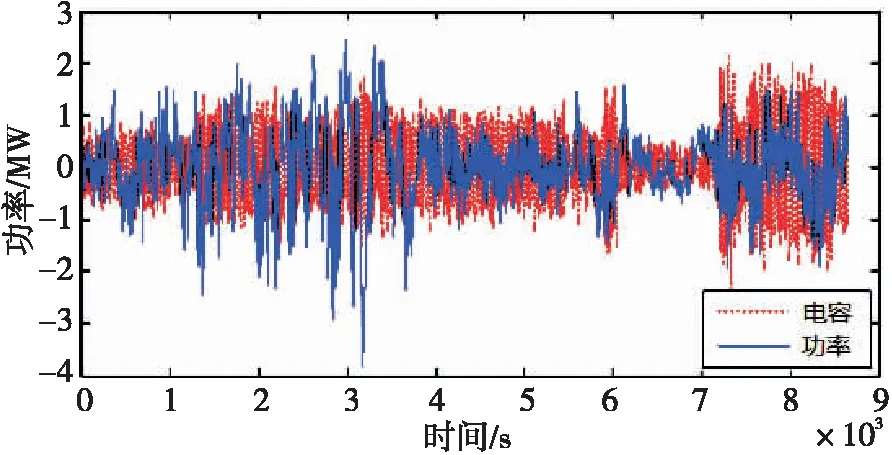
图7 电容器组与输出功率变化曲线

图8 不同功率平滑算法下输出变化曲线

从图8看出，超级电容采用小波算法与MUSIC算法联合的功率调节方法能及时进行电网功率修正，使电网功率状态保持在较合理范围内。

6 结论

本文在风力发电分布式接入电网模式下，选取超级电容器组作为储能装置，并给出在双馈发电机模式下的风电储能装置控制系统。该系统利用小波变换算法的多分辨率特点，得到更具周期特性的低频信号分量和高频信号分量；在构造的模型中将设定的风力发电所输出的目标功率作为阈值，并将在线监测得到的风力发电所输出的功率经过小波变换和MUSIC算法，得到算术平均功率密度，其值与设定阈值比较，从而控制超级电容器组的充电和放电状态。所设计的控制系统利用电容器组反应速度快的特点进行风电功率波动平抑，有利于电网稳定性的快速调节。