基于改进型轴套力的机器人钢丝绳传动动力学建模与仿真

贠今天 ，赵子业 ，左 鹏 ，夏 雨

（1.天津工业大学 机械工程学院，天津 300387；2.天津工业大学 天津市现代机电装备技术重点实验室，天津 300387）

随着机械向高速、轻量化方向的发展，钢丝绳传动因其具有强度高、弹性好、自重轻及挠性好等优点被广泛应用于机器人传动.

钢丝绳传动作为机器人的一种传动方式已经成为国内外的研究热点问题之一.国内的研究中：2006年，金国庆[1]提出了钢丝绳传动的线槽匹配，分析了加工精度，以及对传动时滑移问题的理论计算，但其未对钢丝绳传动进行动力学仿真分析研究；2010年，罗护等[2]提出了一种新型的钢丝绳传动结构的线槽匹配以及设计，但并未深入分析钢丝绳传动过程的动力学问题.2010年，王定贤等[3]提出了钢丝绳建模的几种方法，但并未结合具体应用领域.2013年，董达善等[4]基于adams进行钢丝绳建模仿真研究，但其只进行了运动学分析，未进行动力学仿真分析.Guo[5]主要研究了一种钢丝绳精确位置控制的策略，但未对动力学进行分析研究，可能会造成精度差等误差.国外的研究中：Krishnadev[6]通过一系列实验测得了拉索类钢丝绳失效重力的临界值，但未对传动位置的钢丝绳进行失效速度的实验.

目前，针对钢丝绳精密传动分析大多是以整个系统为研究对象，而不是针对钢丝绳传动本体.虽然该类研究都对钢丝绳传动进行了分析研究并对钢丝绳传动进行运动控制，但均未得出针对钢丝绳传动过程中的动力学仿真数据，不能进行精确动力学控制.针对以上问题，本文提出一种基于adams建模的钢丝绳动力学建模方法，对钢丝绳精密传动进行了系统分析，解决了钢丝绳传动过程中的动力学问题，提高了钢丝绳传动过程中的动力学控制精度.

以下是几种钢丝绳建模常用方法.离散柔性体建模：该方法是adams提供的小变形柔性体的直接建模方法.利用多个离散圆柱体通过横梁力（beam）连接形成柔性的钢丝绳，该方法能直接操纵模型参数，但是这种方法不能实现在滑轮之间添加接触力和摩擦力，只能用于简单的拉索类钢丝绳建模[7].连续柔性体建模：该方法针对的是大柔性体钢丝绳建模.利用有限元软件生成MNF模态中性文件，再导入动力学软件adams中生成钢丝绳柔性体，该方法可以分析钢丝绳的变形，震动以及动力学模型，该方法进行仿真分析的精度很高，但是这种方法不能模拟钢丝绳与滑轮之间的缠绕问题，仿真具有局限性[8].轴套力建模：该方法是利用轴套力连接离散的一个个小圆柱体进行建模方法.利用该方法可以模拟钢丝绳的拉伸，弯曲，缠绕，震动以及和其他物体之间的相互摩擦力，仿真精度高，应用较广泛.但是钢丝绳离散化数量，轴套力数量，接触力以及摩擦力的数量影响仿真时间，仿真速度慢，对硬件要求高[7].基于多线段的建模：该方法是利用齿轮副模拟钢丝绳与滑轮或者电动机主轴连接的一种建模方法.利用该方法可以有效地传递力并实现钢丝与滑轮之间的同步运动，但是不能反映钢丝绳振动对系统的影响，也无法实现钢丝绳的多圈缠绕，仿真精度较差，应用受限[7-9].基于cable工具箱的建模：该方法是利用若干个离散的刚性球体通过移动副、单向力以及转动副约束来模拟的建模方法.基于cable工具箱的建模方法无论计算还是仿真都比较简单，但是它一般应用于钢丝绳是一个连接部件，而不适用于传动部件[10].

综合上述方法的优缺点以及所对应的应用领域，本文提出一种改进型的轴套力建模方法，针对机器人钢丝绳传动进行动力学建模.

1 改进型轴套力建模方法

在钢丝绳实体建模过程中，各小圆柱段通过bushing轴套力连接.Bushing力通过6个分量连接2个小圆柱段，分别是3个力和3个力矩，在2个小圆柱段之间施加柔性力连接[11]，如图1所示.

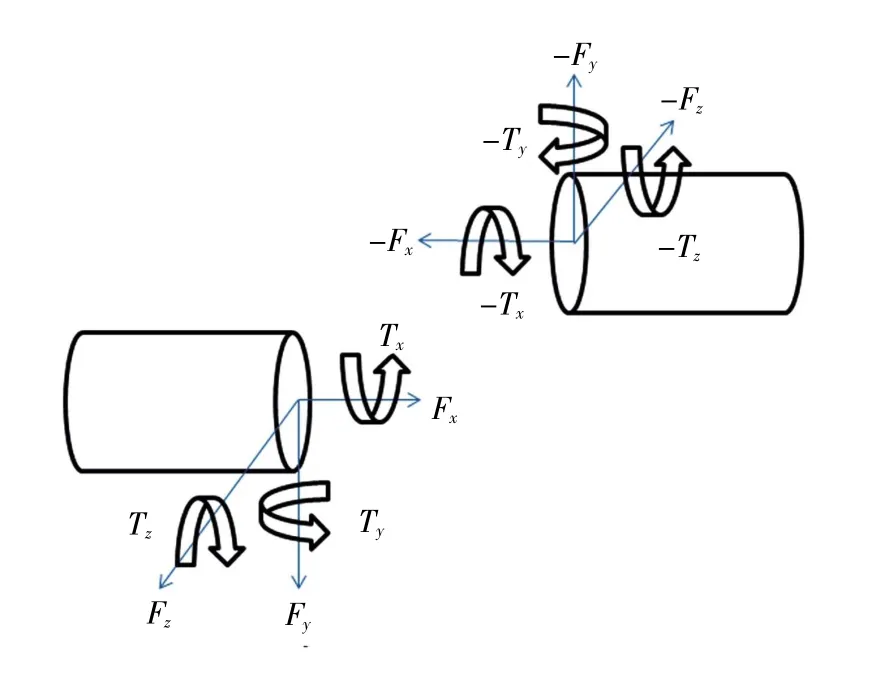
图1 钢丝绳轴套力模型Fig.1 Wire rope bushing force model

在图1中2个小圆柱段的中心建立表示力和力矩的坐标标记i和j，轴套力计算公式为：

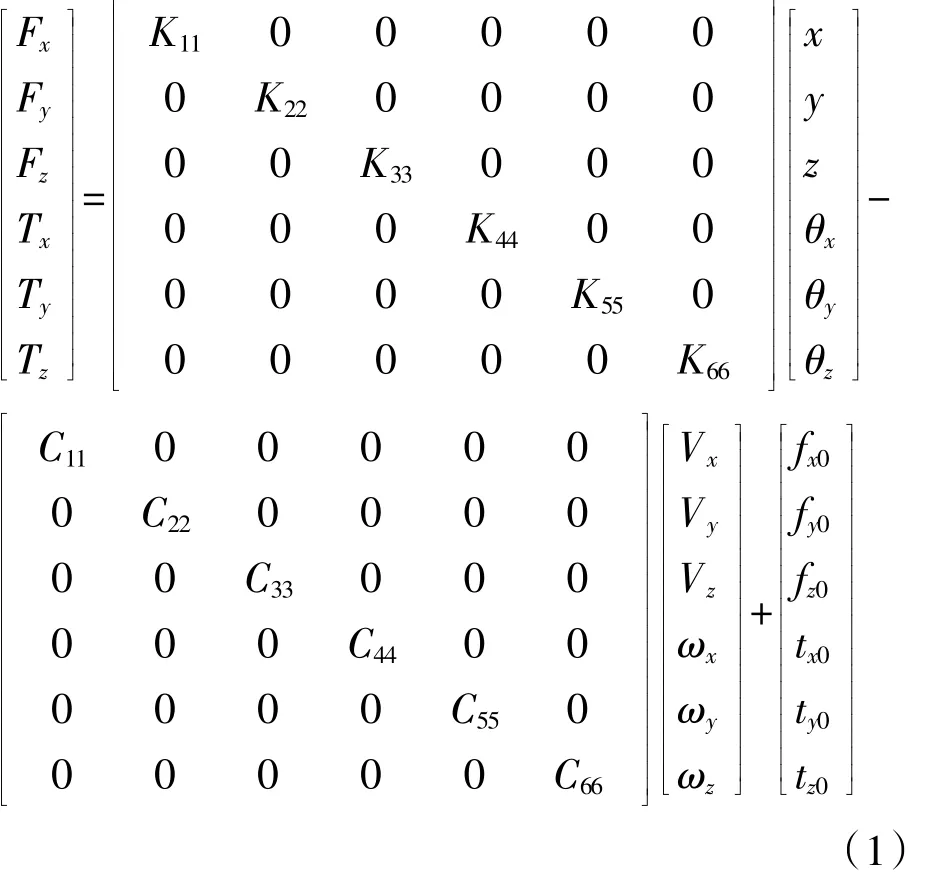
式中：K11为拉伸刚度系数；K22、K33为剪切刚度系数；K44为扭转刚度系数；K55、K66均为弯曲刚度系数；x、y、z分别为第1个构件上的i-Marker坐标系相对于第2个构件上的 j-marker坐标系的相对位移；θx、θy、θz表示i-marker坐标系相对于j-marker坐标系的相对角位移；Vi、ωi分别为 i-marker相对于 j-marker的相对速度和相对角速度；fi0、ti0均为预加载荷.

轴套力的反作用力Fj和Tj力矩的计算如下：

式中：δ为钢丝绳的形变量；Fi、Ti分别为构件1上的轴套力和力矩.

式（1）中刚度系数的计算公式如下：

式中：E为钢丝绳弹性模量，取E=200 GPa；G为钢丝绳剪切模量，取G=80 GPa；d和A分别为钢丝绳直径和横截面积，取d=2 mm，A=3.14 mm2；L为离散化钢丝绳长度，在试验中L=4 mm.

钢丝的阻尼系数为1～10之间的某个能真实的反应钢丝绳的实际运动的数值，本文选取的阻尼系数为5.

在adams中，要将一段钢丝绳离散化若干的小圆柱时，利用几何建模，工作量太大，而且容易出现错误，因此本文编写了大量基于adams二次开发的宏命令[12]，利用编写的宏命令语句可以准确地完成离散钢丝绳的复制、移动、连接、离散钢丝绳之间添加轴套力、离散钢丝绳与轮子之间添加接触力和摩擦力等建模问题.

2 基于改进型轴套力的钢丝绳动力学仿真研究

在机器人系统中，钢丝绳传动起着至关重要的作用，钢丝绳传动的准确性直接影响机器人的控制精度，如果钢丝绳传动效率较低，速度波动较大，这必将导致机器人产生较大的运动误差.然而钢丝绳传动仿真因其复杂性，制约了在钢丝绳传动方面的研究.本文基于改进型的轴套力建模方法对钢丝绳传动进行了动力学仿真研究，并对钢丝绳模型进行优化，以达到较好的传动效果.

分析不同传动结构的传动精度问题，本文设计了2种传动方式，分别是单圈钢丝绳传动和多圈绕线槽轮传动，通过仿真比较，获得传动效率较高且较平稳的缠绕方式，为控制策略及控制方法提供可靠依据.

2.1 单圈钢丝绳传动

（1）建模过程.在此仿真中采用了432 mm长的钢丝绳，把钢丝绳分成108段小圆柱体，主、从动轮直径为25 mm.

①在adams中建立一个圆柱段，然后通过编写宏命令实现钢丝绳的复制并移动.②通过添加bushing，使每个小圆柱体通过柔性连接，构成一段钢丝绳.③通过计算使钢丝绳在中间位置弯曲出一个半圆，弯曲半径12.5 mm，此半圆缠绕在从动轮上.此时钢丝绳分为2部分，把第2部分的钢丝绳进行坐标变换.因为在添加轴套力时它们的接触面已经固定，再弯曲之后为保障接触面还是原来的，需要进行旋转180°，然后平移.最后对缠绕在主动轮上钢丝绳进行弯曲，使其形成一个封闭形状的钢丝绳.最后在首尾2个小圆柱段进行手动添加bushing，形成了1个封闭力的钢丝绳.④在adams中建立主动轮、从动轮和预紧轮，主从动轮是3个圆柱通过布尔加形成的一个整体，所以在添加接触力和摩擦力的时候，主动轮和从动轮各需要添加3次，分别对应不同的圆柱面.预紧轮在靠近主动轮的位置，如图2所示.

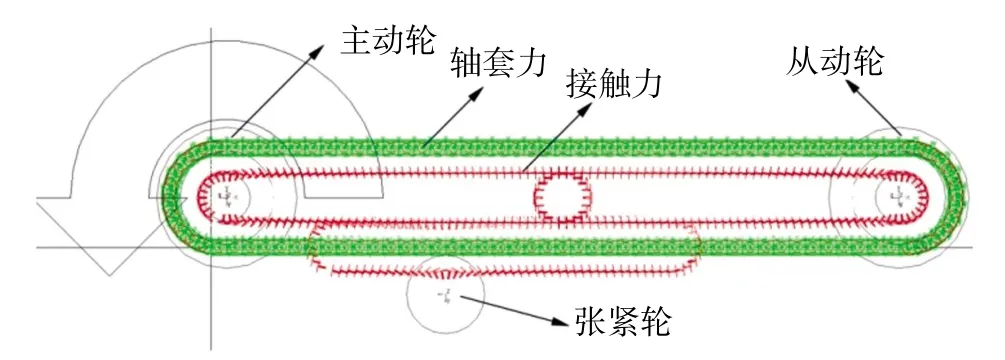
图2 单圈钢丝绳传动adams模型图Fig.2 Adams model of single circle wire rope drive

（2）接触力定义以及设置.在建模过程中接触力的设置以及添加起着重要的作用，在adams中接触力一般通过2种方法进行定义，分别是补偿法和冲击函数，但是补偿法参数设置准确度低，所以通常采用冲击函数进行参数设置，接触力的函数定义通过Impact计算，具体定义如下：

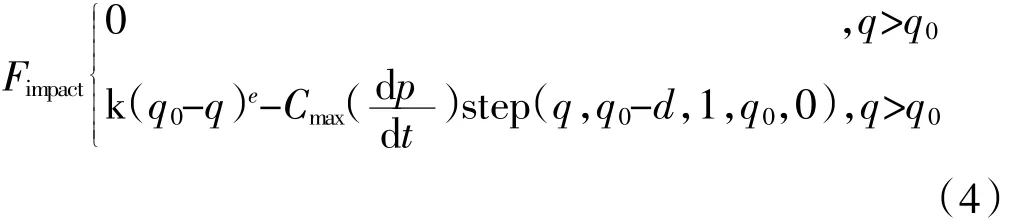
式中：q为两碰撞物体的实际距离；q0为两碰撞物体的初始距离；dq/dt为两碰撞物体间距随时间的变化速率，即速度；k为刚度系数；e为碰撞指数；Cmax为最大阻尼系数；d为切入深度.

公式（4）中的 Step 函数的表达格式 step（x0，x0，h0，x1，h1，），表达式：

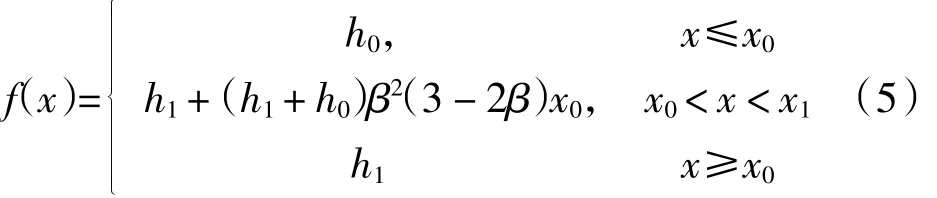
其中β=（x-x0）/（x1-x0）.

（3）接触力参数的设置.①刚度系数K是接触力重要参数之一，在此仿真中采取的是经验公式确定刚度系数，表达式：

在此实验中静摩擦系数为0.3，动摩擦系数为0.1，（钢丝绳动摩擦系数在0.1～0.25之间）.然后修改钢丝绳以及轮子的属性，钢丝绳材料选择铝是因其加工工艺较成熟，而且摩擦力研究较详细；轮子材料选择钢.接下来添加转动副以及固定副，最后在主动轮上施加-5 r/s的转速.仿真5 s，共50步，从动轮速度波动曲线如图3所示.

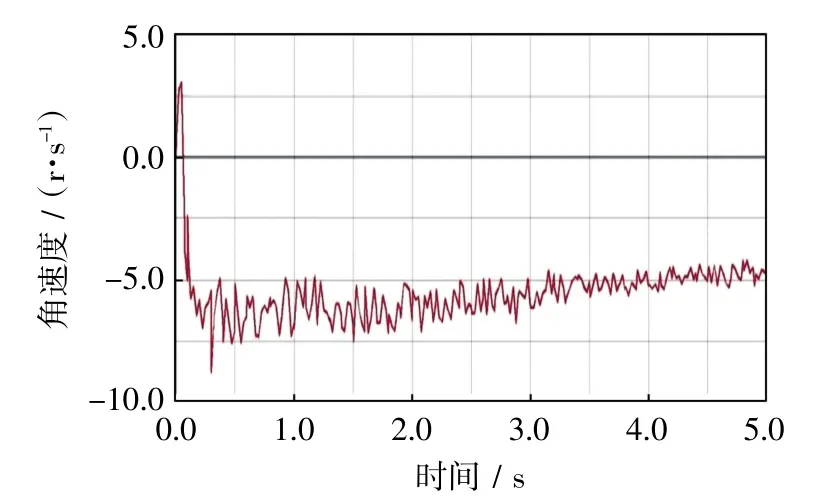
图3 从动轮速度波动曲线Fig.3 Velocity fluctuation curve of driven wheel

（4）仿真结果.通过仿真结果可以看出，刚开始启时，速度很不稳定，有较大波动.接下来速度趋于平稳，速度最后在-4.7 r/s处上下波动.传动效率的计算公式：

通过adams可知输入输出转矩的平均值，代入公式（7）得出传动效率为94%.

（5）总结分析.这种相似于传动带的传动方式在钢丝绳上的应用具有一定的缺陷，缺陷经分析可能来源于两部分，分别是钢丝绳与主动轮的相对滑动以及钢丝绳相对从动轮的相对滑动，导致了传动效率较低，为此针对缺陷提出了改进方案.

2.2 多圈绕线槽轮传动

为了增大传动效率，在原有基础上改进传动结构，从而提高传动速度，在此模型中根据表1，采取的是主动轴为光轴，从动轴为螺旋槽.

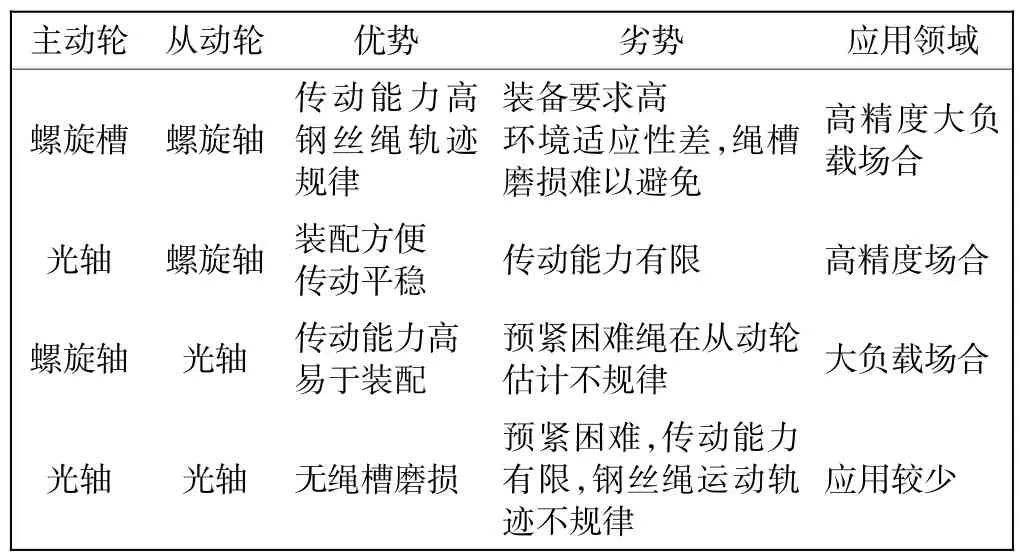
表1 主、从动轮选择Tab.1 Selection of driving wheel and driven wheel

（1）建模过程.在第2个实验中，同样采用432 mm钢丝绳进行仿真，分成108段小圆柱，主从动轮直径25 mm.①先建立1个小圆柱段，然后通过宏命令进行复制，移动.②不同于第1个模型，此模型需要进行复杂的坐标变换，钢丝绳需要进行盘旋且需要移动.③在这个模型中区别于第1个模型，adams建模具有局限性，对于复杂的零件可以通过三维软件进行辅助设计，此模型的从动轮就是通过SolidWorks设计从而导出parasolid（x_t）文件，再导入此模型中，通过改变坐标使其相互缠绕.④因为从动轮是从三维软件中导入adams中的，所以在添加接触力以及摩擦力的时候只需要添加一次.

接触力的定义以及系数跟实验1相同.在钢丝绳的首尾两段，对其进行了固定，把第一个小圆柱跟最后一个小圆柱固定在主动轮上，这样是为了模拟另一种钢丝绳缠绕接头.模型如图4所示.

图4 多圈绕线钢丝绳传动adams模型图Fig.4 Adams model of multi-turn wire rope drive

在此实验中静摩擦因数为0.3，动摩擦因数为0.1，（钢丝绳动摩擦因数在0.1～0.25之间）.然后修改钢丝绳以及轮子的属性，钢丝绳材料选择是aluminum，轮子材料选择是steel.接下来添加转动副以及固定副，最后在主动轮上施加-5 r/s的转速.仿真5 s，共50步，从动轮速度波动曲线如图5所示.

图5 从动轮速度波动曲线Fig.5 Velocity fluctuation curve of driven wheel

由图5可知，在模型中刚启动时速度波动较大，接下来速度趋于平稳，最后在-4.9 r/s上下波动.根据公式（7），得出传动效率为98%.

（2）总结分析.此仿真通过增大接触面积，从而增大摩擦力来实现传动效率的提高，相比较单圈钢丝绳传动，此仿真的传动效率具有较大的提升，由94%提高到98%，所以多圈绕线槽轮传动具有较高的传动效率.将2种传动方式从动轮速度曲线进行比较，如图6所示.

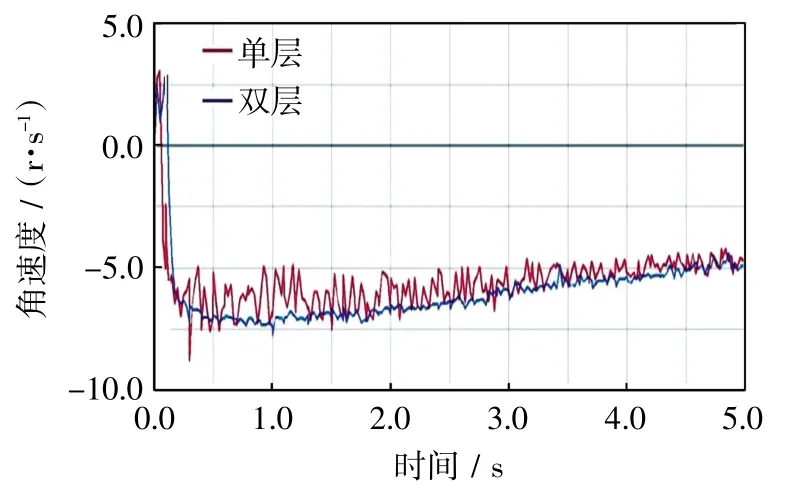
图6 2种传动方式从动轮速度曲线比较Fig.6 Comparison of speed curve of driven wheel of two driving modes

由图6可知，单圈缠绕方式从动轮速度波动较大，而多圈螺旋缠绕速度波动较小，在精密仪器中，速度的波动尽可能减小，这样会提高操作的精确度.

在单圈钢丝绳传动仿真中，仿真之初，施加给主动轮-30 rad/s的角速度，结果从动轮速度波动较大，且传动效率非常低，针对这个现象，对其进行了失效速度的验证.

2.3 钢丝绳传动失效的主动轮速度验证

在2种钢丝绳仿真中，要寻找到从动轮速度失效的主动轮速度区间，在仿真1和仿真2的基础上，进行了几组数据的仿真，对主动轮速度进行增加，每次对主动轮速度增加10 r/s，得出从动轮速度，在5组数据的基础上对其进行二次拟合.如图7所示.

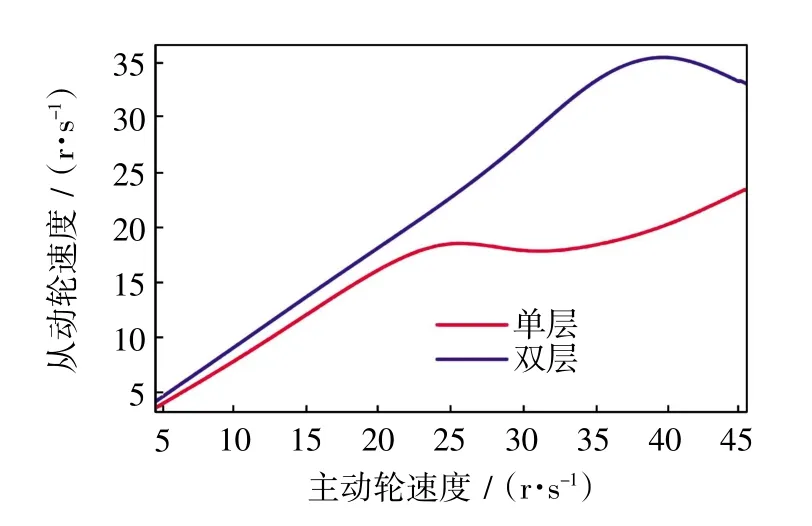
图7 2种传动方式的从动轮速度随主动轮速度变化曲线Fig.7 Speed of driven wheel in two transmission mode varies with speed of driving wheel

从图7中可以看出，在单圈钢丝绳传动仿真中，主动轮速度在超过25 r/s之后，从动轮速度开始出现较大波动，故判断失效.而在多圈绕线槽轮传动仿真中，当主动轮速度超过40 r/s时，从动轮速度出现较大的波动，故失效.综上所述，多圈绕线槽轮传动中主动轮速度范围较广.

3 结语

本文通过对钢丝绳建模方法的分析研究，提出一种改进型的轴套力钢丝绳动力学建模方法.基于该方法，对单圈与多圈缠绕方式的钢丝绳动力学进行仿真研究，可以得出单圈与多圈缠绕方式的传动效率分别为94%和98%，并且多圈缠绕方式的传动速度更加平稳.同时对两种钢丝绳主动轮不同速度的仿真研究，得出较好的传动速度区间.本文在仿真的过程中，利用adams宏命令进行建模，提供了钢丝绳建模的一种准确方法并减少了繁琐的工作量，为今后的钢丝绳动力学分析研究提供快速建模方法.