三角剪切断层传播褶皱应变分布

张伟康，何登发

[中国地质大学(北京) 能源学院，北京 100083]

褶皱与断层作为构造地质学中最典型的构造样式，二者常常出现在同一构造单元中，且具有密切的成因联系与伴生关系。Suppe[1]、Suppe和Medwedeff[2]假设参与变形的地层依照面积守恒、层厚不变等原则，使用平行膝折褶皱作用建立了以尖棱状褶皱或箱状褶皱为特点的断层转折褶皱和断层传播褶皱的几何学与运动学模型，首次定量表征了前陆褶皱-冲断带中褶皱形态与断层样式之间的几何关系与成因联系[3]。但前陆褶皱-冲断带中还广泛发育着如图1所示的变形样式，褶皱样式不再遵循平行褶皱原则，具有光滑而连续的转折端，褶皱两翼呈现出明显的不对称性，前翼狭窄、陡峭甚至倒转，而后翼宽缓；地层连续变形，不发育统一的倾角域，地层出现增厚或减薄现象；断层下盘卷入变形，发育与断层上盘背斜成对出现的向斜构造；断层终止于褶皱核部，褶皱也随着趋向于断层，样式更趋紧闭[13-15]。这种构造样式更加明确地显示出褶皱与断层之间具有密切的成因联系[14,16-18]。

为了描述此类褶皱与断层的几何关系，Erslev提出了“三角剪切断层传播褶皱”的概念并初步建立了相关的几何学与运动学模型[19]。在此模型中，断层端点前方变形不再为轴面控制，而是将褶皱变形限定于一个向上变宽的三角形连续剪切变形带内，三角形顶点固定在断层端点，此变形带随着断层端点的向前传播也不断向前迁移，从而形成光滑的褶皱转折端和更复杂的变形特征[19-20]。

为了定量描述三角剪切变形带内的变形过程，建立更完善的三角剪切运动学模型，许多学者通过具体描述参与变形的标志点速度的连续变化，建立三角剪切带速度场，进一步实现对位移场的模拟，从而完成三角剪切断层传播褶皱的正演和反演的数值模拟。Hardy和Ford建立了三角剪切带的速度模型，提出了断层三角剪切带内褶皱形态受控于断层传播量和断层滑动量之比(P/S)[21]；Hardy和McClay使用粘土对三角剪切断层传播模型展开构造物理模拟实验，对模型进行合理性检验，同时表明此模型还可应用于正断层传播褶皱几何形态的正演模拟[22-24]；Zehnder和Allmendinger基于三角剪切带内参与变形的地层面积守恒，提出了二维速度场连续性方程，并以此为基础描述了非线性变化的速度场特征[25]；Cristallini和Allmendinger、Cardozo分别将二维速度场描述方法拓展到三维空间，在三维速度场连续性方程基础上，进行了三角剪切断层传播褶皱三维空间中的几何特征描述与运动学模拟[26-28]。

三角剪切带内满足物质连续性的速度分布模式的确立，明确了标志点间相对位置的变化，使得褶皱变形过程中应变分布的定量表征成为可能[29-32]。这是对平行膝折褶皱作用的重要补充，使用速度连续变化的三角剪切模型可以解决膝折带褶皱模型中地层经活动轴面时运动方向突变的问题[30]。这如同将控制膝折带变形的轴面“打开”，可以进一步观察岩层经轴面时速度连续变化的细节和应变分布的特征，进而为变形区裂缝预测与次级断裂的发育提供研究思思路与手段[33-34]。

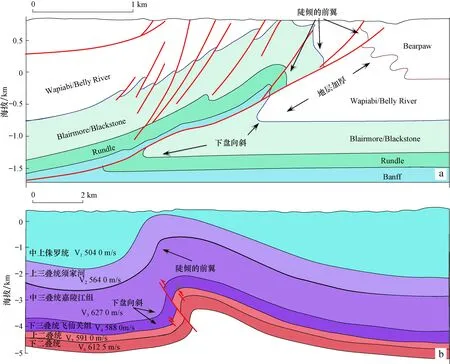
图1 典型的三角剪切断层传播褶皱Fig.1 Typical tri-shear fault propagation foldsa.加拿大落基山脉Turner Valley背斜剖面[4-7]；b.四川盆地卧龙河背斜地质模型[8-12]

本文采用Jin和Groshong改进的满足面积守恒的非线性三角剪切带速度分布模式[23]，应用柯西方程计算三角剪切带内的瞬时应变速率，讨论三角剪切带内应变分布规律，并借助MATLAB软件大量的功能函数和强大的数据处理能力，实现对三角剪切断层传播褶皱的正演模型的开发，并分别进行不同三角剪切角和断层传播量和滑移量之比(P/S)条件下的正演模拟，反映断层生长与褶皱变形过程中构造几何特征随时间的变化规律；通过不同阶段三角剪切带内应变椭圆形态变化，反映褶皱发育过程中断层前翼应变的分布差异，讨论三角剪切角与断层传播量和滑移量之比(P/S)对三角剪切断层传播褶皱形态与应变分布的影响。

1 三角剪切带速度场模型

三角剪切断层传播褶皱模型的基本几何学模型如图2所示，三角剪切带固定于断层端点前方，上盘岩层沿断层面作刚体运动，速度为v0，经三角剪切带上盘边界后逐渐地非线性减少，于下盘边界趋于0，具有整体内部连续变形特征。因此，须建立固定坐标系ζOη描述断层端点的向前传播，其坐标原点为起始断层端点，和以当前断层端点为原点的XO′Y活动坐标系，ζ轴、X轴均与断层延伸方向一致。

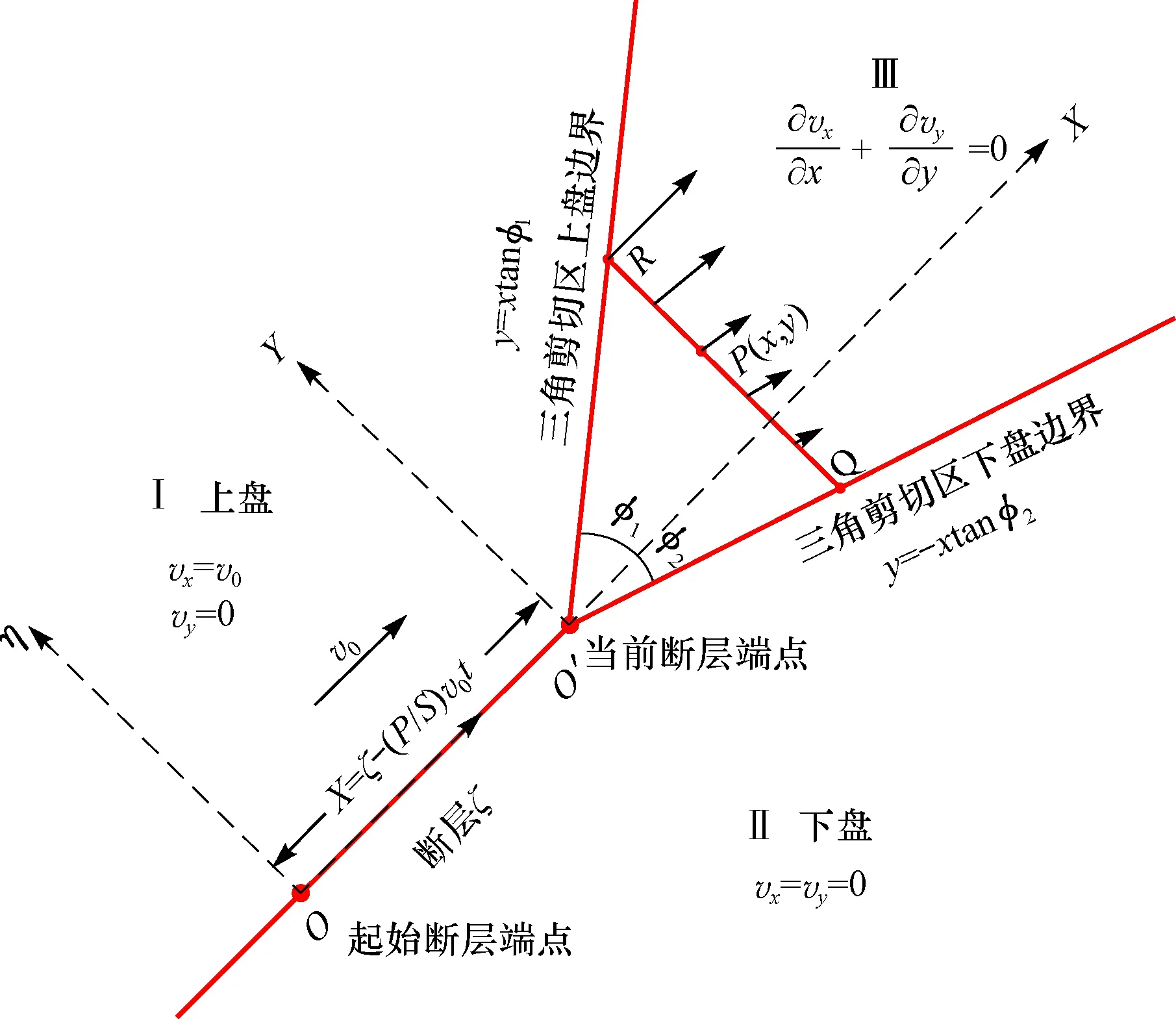
图2 三角剪切区速度分布模型及坐标系Fig.2 Velocity distribution model of the tri-shear zone and its coordinate system used in the text

三角剪切带沿X轴被分为φ1、φ2，二者在构造物理模拟实验和天然的褶皱形态中，常具有非对称的特点[35]。

断层端点附近速度场可分为3个区，Ⅰ区、Ⅱ区速度为常量，Ⅰ区位于断层上盘，平行于断层面呈刚体运方动；Ⅱ区位于断层下盘，处于静止状态；Ⅲ区处于断层端点前三角剪切带内，岩层连续，无明显破裂，为协调Ⅰ区和Ⅱ区差异运动而表现出围绕断层端点的褶皱变形，速度表现为由上盘边界向下盘边界发生旋转并且逐渐减小，最终趋于零，其速度场可表示为：

(1)

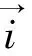
vx=vo;vy=0;y=xtanφ1(上盘边界) (2)

vx=vy=0;y=-xtanφ2(下盘边界)

(3)

三角剪切断层传播褶皱主要发育在脆韧性过渡带之上，变形过程中无明显的物质迁移转化，在二维剖面中，假设岩层仅在平面内发生运动，那么在三角剪切带内将满足物质守恒；若岩层不可压缩，则满足面积守恒，由此可得，三角剪切带内速度场散度div(v)为零，即三角剪切带速度的连续性方程为：

(4)

满足式(4)速度连续性方程的速度分布有很多种，但并非所有的速度分布都符合具有复杂岩石力学性质的岩层在构造应力作用下真实的变形过程[35]。当假设vx呈幂函数形式时，模拟得到的褶皱样式能与构造模拟实验和天然的三角剪切传播褶皱较好匹配[36]，且形式简单，可视为褶皱形态的一级近似。目前，在常用的构造模拟软件如Midland Valley发行的MOVE商业软件、康乃尔大学Rick Allmendinger编写的Fault-Fold-Forward软件在三角剪切断层传播褶皱模块均采用这样的算法，本文采用的是上述软件算法基础上Jin和Groshong提出的改进算法，此算法的优点在于可描述关于X轴非对称的三角剪切区速度分布特征，并明确了决定vx分布方式的参数r的表达式。三角剪切带内vx的幂函数的一般形式为：

(5)

式中:LPR、LQR为PR、QR之间的距离,m;m1=tanφ1;m2=-tanφ2；参数r用于表征vx的分布特征，当r=1时，vx将关于y呈线性减小，随着r的增大，速度将呈非线性变化，vx的梯度将随着x的增大而增大,如图3所示。联立式(4)和式(5)，并对dvy不定积分，考虑边界条件，可得：

由此，影响三角剪切带速度场分布的主要参数为三角剪切角(φ1+φ2)，其速度场以矢量形式表示为：

在三角剪切断层传播褶皱模型中，因三角剪切带将随断层端点的向上传播而不断迁移，这将导致不断有断层端点前方岩层卷入变形，也将有岩层退出三角剪切带的变形域，由三角剪切带下盘边界退出变形区的岩层将保持静止，由上盘边界退出变形区的岩层将平行于断层作刚体平移。由此可见，断层端点的传播方式将直接决定卷入变形的岩层范围与变形区内岩层的累计变形时间。因此，还需建立ζOη固定坐标系与XO′Y活动坐标系之间的关系：

(9)

式中:P即为断层端点的传播量，为断层最大断距;S为岩层沿断层滑移量，可表示为，S=v0t。在使用地震剖面进行构造解释时，大型断层位置处与强变形带资料信噪比往往较低，同相轴反射连续性差，使得断层端点传播量的估算误差较大，而滑移量却可以通过构造反演、使用平衡剖面技术得到较为准确的估算。因此，在构造正演模拟过程中设置P/S值与滑移量(S)以估算断层端点传播量(P)，减少误差。

以初始相互平行的标志点来模拟未变形的水平岩层，通过追踪这些标志点在式(8)与式(9)速度场控制下的瞬时速度分布特征，对速度进行时间积分，或对微小时间间隔内标志点位移进行累加，可以模拟得到断层端点前方产生的褶皱形态。图4显示了在断层倾角为45°，滑移量S=0.16，P/S=1.5，φ1=40°，φ2=30°条件下，地层标志点速度矢量图与三角剪切带褶皱变形的叠加，三角剪切带内速度不仅减小，方向发生旋转，而且由于r>1，在经过X轴后，其速度变化更为迅速。

2 三角剪切带应变分布

在三角剪切带模型中，岩层无显著的体积变化，即变形前后，岩层均连续变形。变形过程中，位移亦为连续分布，由此可以认为应变也应是连续的、相容的，其应变应满足应变相容方程为：

(10)

否则，将出现岩层的破裂或嵌入现象。这是连续变形的构造模型应满足的必要条件，可以作为检验模型合理性的标准之一。膝折带褶皱模型的缺陷即通过轴面的岩层速度大小不变、方向瞬间改变，在轴面处岩层变形强烈，但两侧均无应变，应变不连续，这也使得该模型无法描述岩层褶皱过程中的应变分布。而三角剪切模型相较于平行膝折褶皱作用的优势体现在岩层速度变化更为连续，使得断层端点前方褶皱形态更为光滑，变形也更为连续。

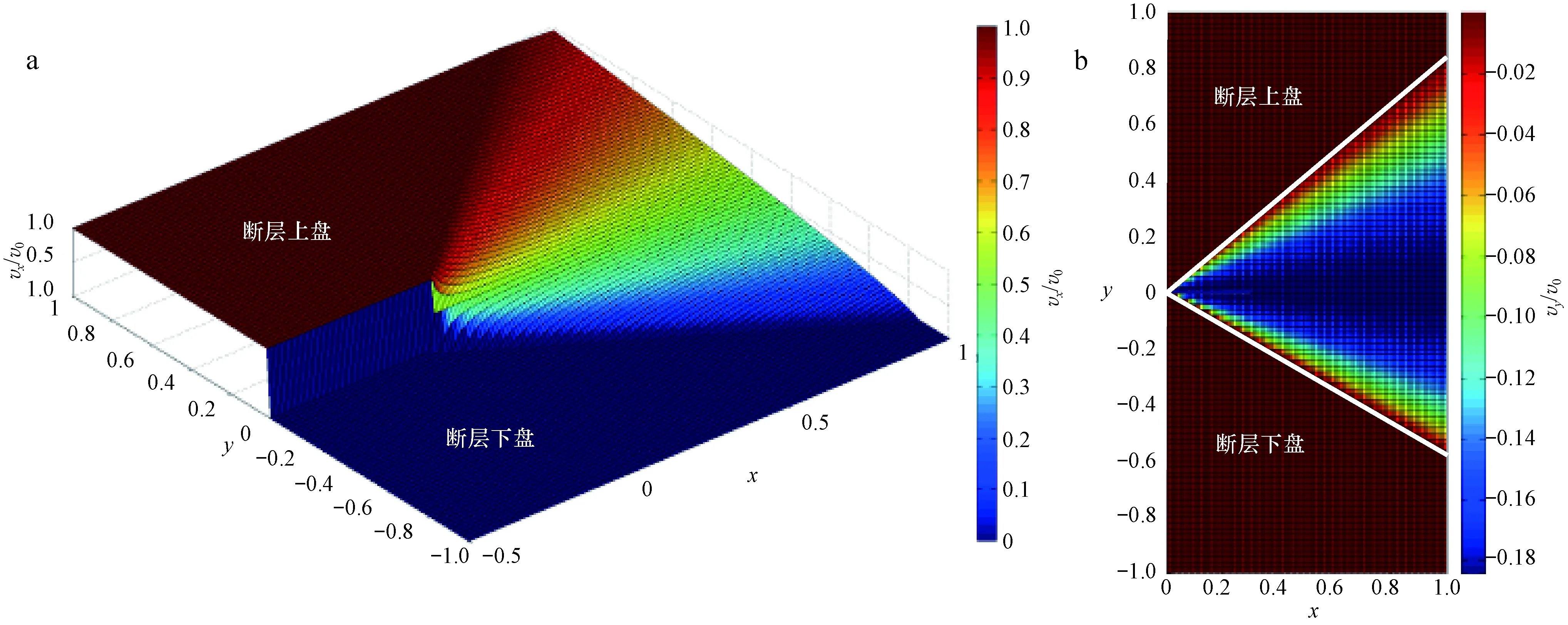
图3 三角剪切区速度分布(φ1=40°,φ2=30°)Fig.3 Velocity distribution in the tri-shear zone(φ1=40°,φ2=30°)a.vx分布；b.vy平面分布

图4 地层速度矢量与褶皱变形的叠合Fig.4 Velocity vectors for the asymmetric vx field and related deformation

当模型中速度分布确定后，各质点间相对位移确定，进而可应用柯西方程描述三角剪切带内瞬时变形特征，包括沿活动坐标系坐标轴方向的线应变速率和剪应变速率。若已知变形持续时间，即可计算三角剪切带累计应变量。

(11)

(12)

(13)

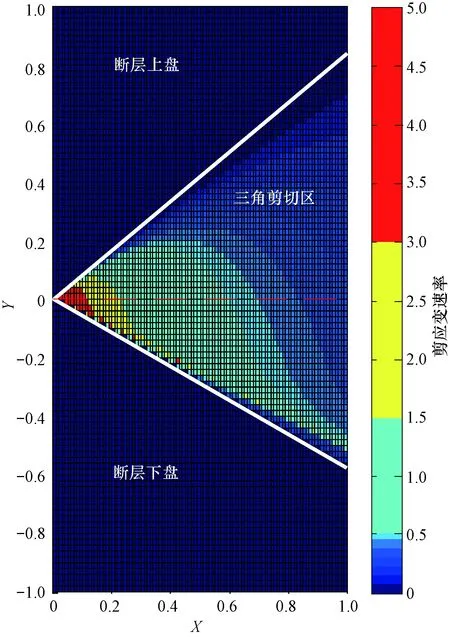
图5 三角剪切带剪应变速率分布Fig.5 Distribution of shear strain rates in the tri-shear zone(φ1=40°，φ2=30°，vx=1；X轴位置粉色虚线为图6的位置。)

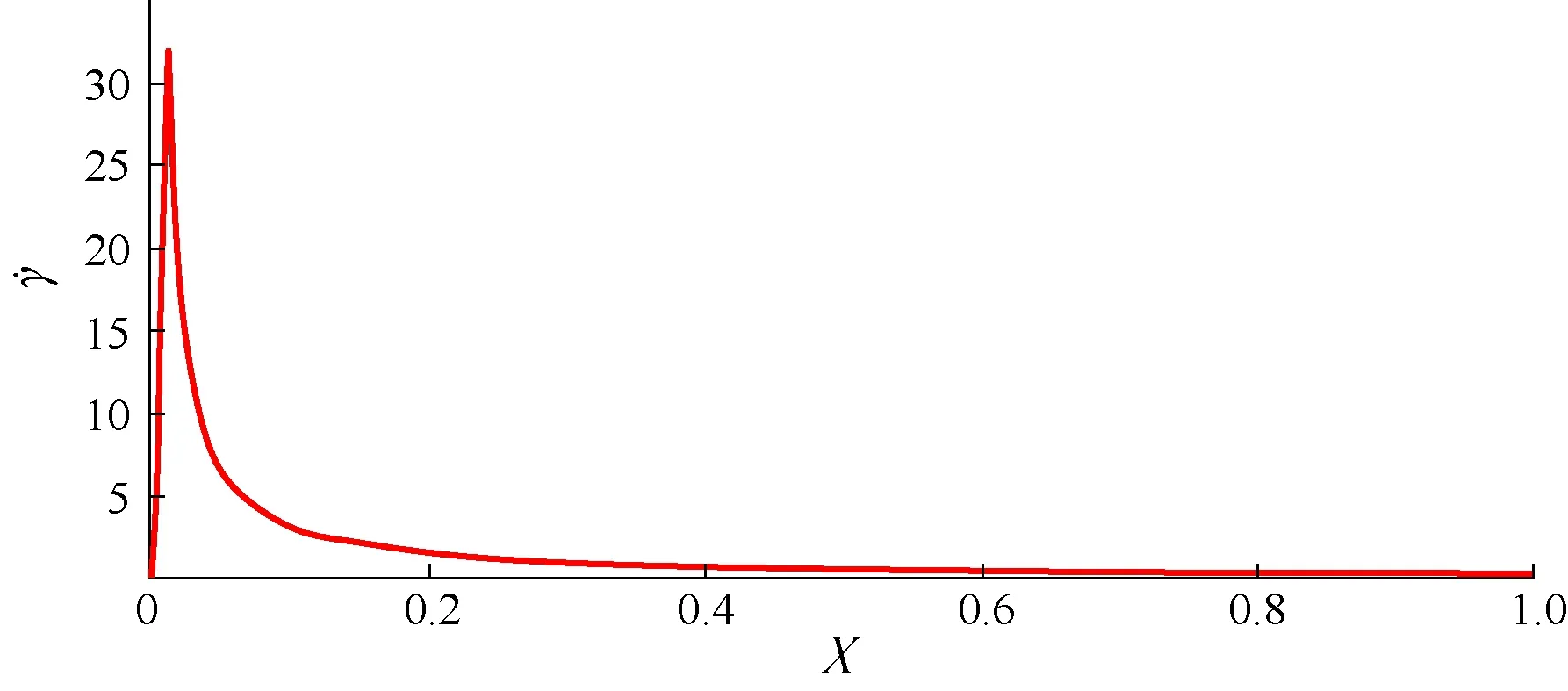
图6 沿X轴剪应变速率分布Fig.6 Distribution of shear strain rates along Axis X

3 讨论

3.1 三角剪切角对褶皱几何形态和应变的影响

为反映参数变化对三角剪切模型褶皱变形与应变的影响，研究采用控制变量法，对同一断层设置不同的三角剪切角，断层倾角45°，P/S=0.5，r=1.5，三角剪切角分别为20°，40°和60°，在相同滑移量下，其变形特征如图7所示。

从模拟结果可以看到三角剪切角的大小直接决定了断层端点前方褶皱的宽度。若三角剪切角较小，在狭小的变形域内，为协调变形，地层须更强烈的旋转，其褶皱翼部陡峭；在相同滑移量下，随着三角剪切角的增加，卷入变形的地层范围迅速增加，褶皱更为开阔、平缓；在断层附近应变椭圆长轴逐渐趋向于平行断层的方向，在断层端点变形最强，出现地层增厚的现象，应变逐渐向外减弱。

图7 不同三角剪切角褶皱形态和应变分布Fig.7 Fold geometry and strain distribution for varying tri-shear apical anglesa，b，c分别对应断层三角剪切角为20°，40°，60°

3.2 断层传播量/断层滑动量比值(P/S)的影响

为表明P/S值的变化对三角剪切断层传播褶皱形态与应变的影响，分别对同一断层，倾角45°，三角剪切角60°，r=1.50，进行P/S分别为0.5，2.5和5.0的模拟，其变形特征如图8所示。

当P/S很小时，岩层具有充分时间在断层端点前方累积应变，发生显著的旋转和变形，在断层下盘出现明显的向斜构造，地层增厚显著，具有韧性变形特征；随着P/S增大，断层端点向上传播速度更快，断层快速切过地层，缩短了应变累积时间，三角剪切带内累计变形减小，使得下盘向斜逐于平缓，地层增厚现象减弱，但在上盘边界开始出现光滑的背斜枢纽；当高P/S时，断层端点快速向前传播，迅速形成宏观破裂面，地层无明显增厚、变形，整体上表现出更明显的沿断裂面的块体滑移。

在断层端点周围始终为变形最强烈区域。随着三角剪切带不断向上传播，将不断有岩层从上盘边界与下盘边界退出三角剪切带，在断层上盘形成光滑的背斜转折端，在断层下盘的形成向斜，这些构造变形为早期变形特征。围绕着断层两侧，岩层具有递进变形特点。

图8 不同P/S比值下三角剪切带内褶皱形态和应变分布Fig.8 Effect of different P/S ratios on the fold geometry and stain distribution in the tri-shear zonea，b，c分别对应P/S=0.5，2.5，5.0

3.3 断层传播量/断层滑动量比值(P/S)的意义

随着P/S的变化，褶皱变形样式发生着变化，断层相关褶皱三端元(滑脱褶皱、断层传播褶皱与断层转折褶皱)可能是P/S值由低至高连续变化的结果[9-10]。在不同的构造环境，相同的滑移量下却能产生不同的断层传播量，这是否意味着P/S能够反映不同岩石的宏观变形行为的差异性？考虑模型中断层端点周围区域强烈的应变集中，与岩石断裂力学中裂纹端部的应力集中具有相似的特点，类比岩石断裂力学中裂纹扩展机制讨论断层传播机制。在单晶以及多晶体的微观尺度上，脆性裂纹是原子级尖锐的，裂纹的扩展借助于键的依次断裂来实现；在宏观尺度上，岩石作为多晶多相材料，具有更复杂的结构，其变形过程的形态也更为复杂。在受到平行于断层面方向的剪切作用时，最初在断层端点由于应变集中，在端点前方高应变区形成彼此孤立的微观裂隙，介质仍保持线性性质；进一步加载时，断裂端点应变进一步累加，裂缝密度增加，断裂端部区域呈现非线性性质[37]。最终，由于非线性区内的裂隙间扩展、连通从而导致宏观断裂的向前扩展(图9)。

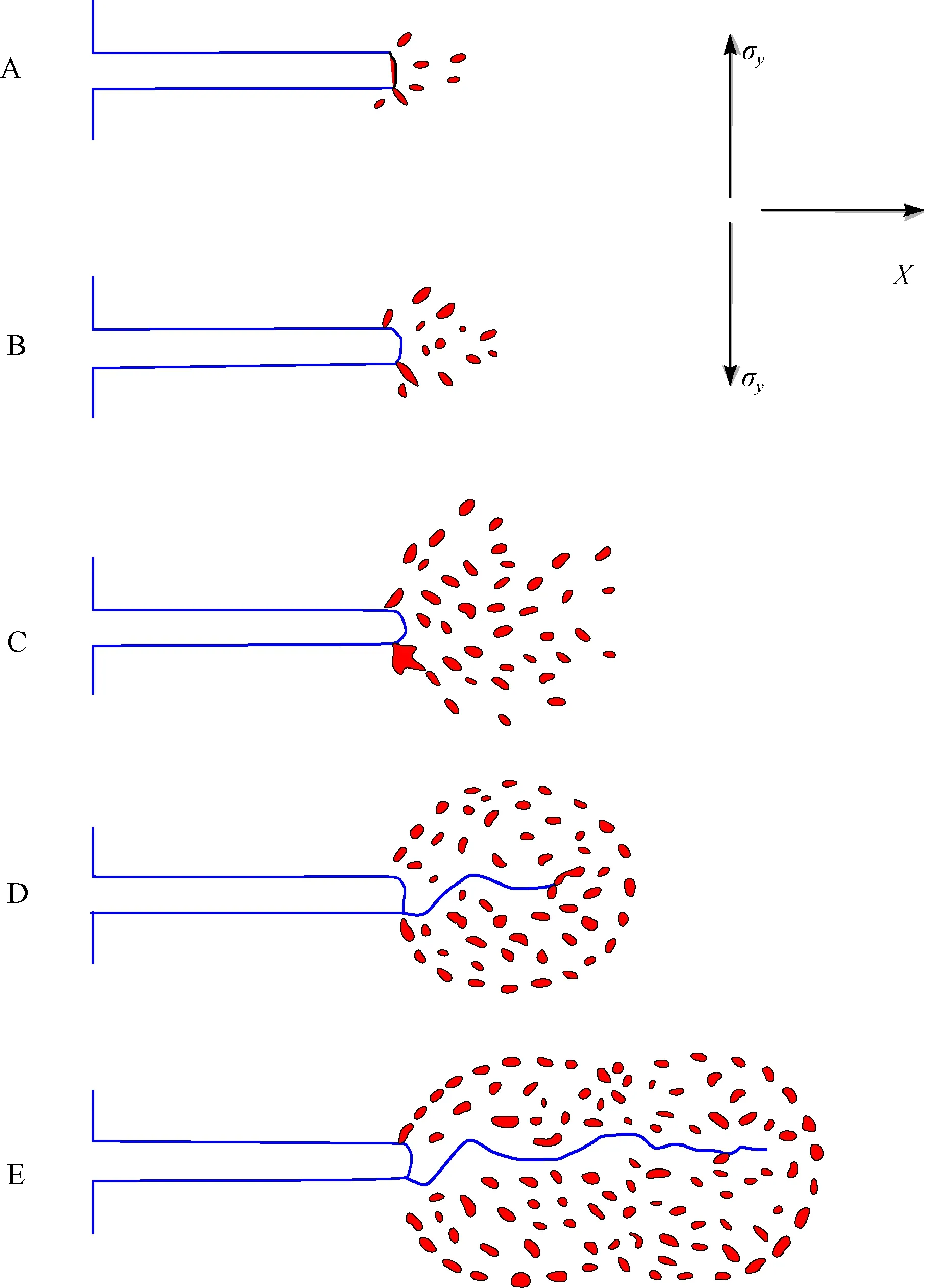
图9 过程区发展过程及其对宏观裂隙扩张影响示意图[39]Fig.9 Development of fracturing zone and its effect on macrofracture expansion[39]

在微破裂大量产生的过程中，若存在应力扰动的疲劳作用或孔隙流体的应力腐蚀作用，断裂可能进入失稳扩展状态[38-39]，Andrews表明平面内剪切裂纹的传播速度可接近在相应介质中P波速度[40-41]，如此，则断层传播量将远远大于滑移量。不同的断裂扩展模式，将直接影响到断裂活动时地层变形特征。

4 结论

1) 基于速度连续性方程建立的三角剪切带速度模型，应满足应变相容原理；通过三角剪切带内标志点速度对时间的积分与断层传播量的计算可模拟三角剪切带褶皱变形形态。

2) 采用满足面积守恒与应变相容原理的速度分布模型，使用柯西方程计算三角剪切带内瞬时应变速率，应变在断层端点前方区域存在应变集中，断层端点变形强烈，趋向断层的区域应变椭圆长轴方向发生旋转、与断层趋向一致，应变随远离断层端点迅速衰减。

3) 影响三角剪切断层传播褶皱应变分布的参数为三角剪切角与P/S比值，三角剪切角决定了褶皱宽度，三角剪切角越小，褶皱愈紧闭，应变也愈集中、强烈；P/S比值影响着卷入变形的地层范围与累计应变的时间，高P/S时，断层迅速传播，地层变形小，形成光滑的背斜枢纽；低P/S时，地层累计变形时间长，变形强烈，断层下盘向斜构造明显，地层增厚。