一种玻璃搬运机器人轨迹规划和优化研究

胡 蓉

（宜宾职业技术学院，四川 宜宾 644003）

1 引言

工业机器人由于其高效、高可靠性及重复精准高等特点，被广泛应用各行各业。但由于搬运目标的差异性，对轨迹规划的具体要求千差万别。将工业机器人应用于玻璃搬运，考虑玻璃尺寸较大且易破碎的特点，能够保证效率的前提下降低抖振来减小破碎尤为重要。

关于轨迹规划的问题，文献[1]对六自由度机械臂轨迹规划与仿真研究；文献[2]对关节空间进行了差值轨迹规划研究；文献[3-5]研究了基于速度和加速度约束的轨迹规划，关于轨迹规划的问题前人也通过其他方式进行了轨迹规划。关于抖动问题，文献[6]分析了对无碰撞-时间最优轨迹规划的影响。文献[7]采用运动学进行轨迹规划并采用进化策略优化。文献[8]利用高阶函数逼近的方法规划来降低抖动。文献[9]提出了一种间隔分析计算的方法，来减小机器人的运动轨迹中的抖动。关于轨迹规划和降低抖动问题前人做了大量研究，有效的从规划算法和优化算法上面解决上述问题，但都存一些缺陷：未将时间和抖动因素综合考虑。为此，将时间和抖动因素综合考虑值得进一步研究。

在前人研究的基础之上，以搬运玻璃的机器人为研究对象，提出采用B样条曲线进行轨迹规划；基于多目标遗传算法以减少单次工序工作时间和降抖动的目标轨迹优化，找到以时间和抖动为最优目标的优化方案，经过遗传算法的优化，使得玻璃搬运机器人的时间和抖动综合达到最优，为实际的搬运作业提供参考。

2 轨迹规划与优化模型

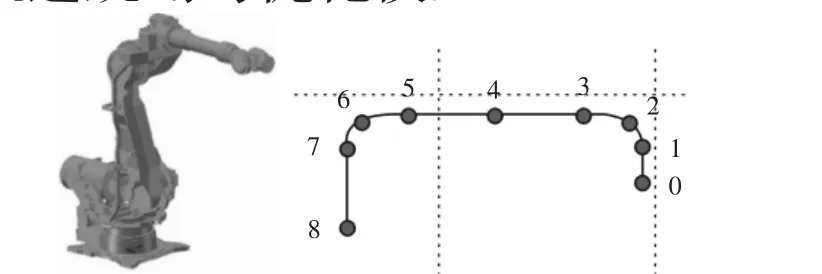
图1 玻璃搬运机器人三维模型及轨迹规划曲线Fig.1 The 3D Model of Glass Handling Robot and its Trajectory Planning Curve

采用六自由度的玻璃搬运机器人为研究对象，其三维模型及轨迹行走的曲线，如图1所示。

六自由度搬运机器人的数学模型构建在文献[10]中已完成，同时通过文献[11]的数学推导，则可得到机器人第j个开关的运动轨迹：

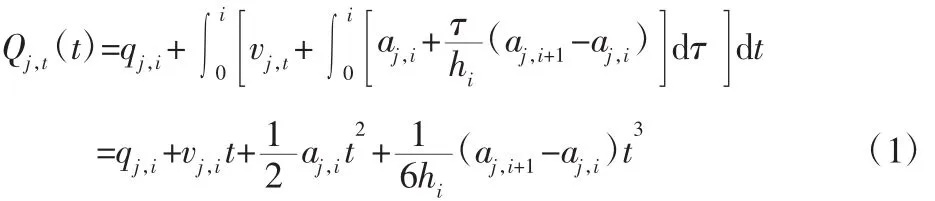
式中：t∈［0，hi］，i=1，2，…，n-1qj，i—关节 j的第 i个插值点的位移；vj，i—qj，i处瞬时速度；aj，i—qj，i处瞬时加速度；aj，i—qj，i处瞬时加速度；hi—两插值点的运动时间。下面进行B样条曲线轨迹规划分析。

由于B样条曲线具有诸多优良性质，如局部支撑性、几何不变性、保凸性、变差减小性等，为此借助该函数的这些特点，采用B样条函数模型表达其工作空间的轨迹规划数学模型可表示为下式：

式中：Qj—控制点—度的基本函数。

确定采用三次B样条曲线，由于B样条曲线在插值点处速度连续的特点，则有：

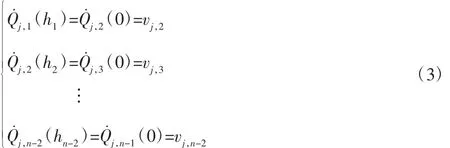
向量；H—（n-2）×（n-2）矩阵，其具体表达式为：

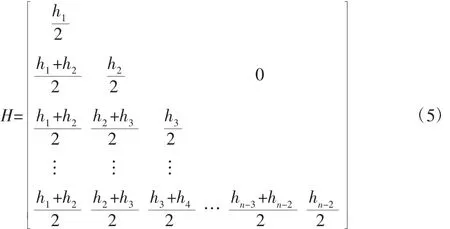
由于函数连续可导，则可以推导出：

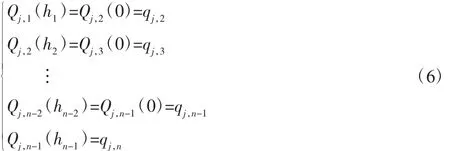
将式（4）代入到式（6），消元 qj，2，qj，n-1后可以得到 n-3 个线性无关的；aj，i—变量的方程，表达成矩阵的形式为H′A=Q。其中：

进一步求解式（7），并将结果带入式（4），则可以得到式（1）中的未知量。那么就可以求得机器人三次样条曲线的轨迹。

3 机器人轨迹的优化模型

3.1 最优时间轨迹规划数学模型

机器人的运动时间即为每个关节做完规定动作后所需要的时间，那么玻璃搬运机器人目标轨迹最优总时间的数学模型就可以表达为：

式中：T—目标轨迹总时间；hi—机器人走完第i段轨迹所需要的时间。

3.2 最小抖动数学模型

3.3 多目标遗传算法搬运机器人最优轨迹规划

同时将机器人搬运时间和单次搬运过程中的抖动量两个因素作为优化对象，并采用权重系数法对时间和抖动进行赋权，数学模型表达为：

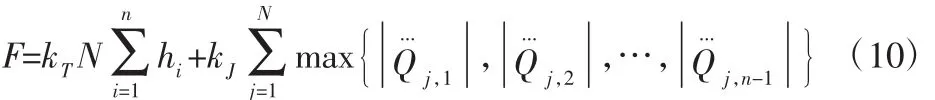
式中：F—考虑搬运时间和抖动量后的轨迹规划参量表达；kT，kJ—时间和抖动的权重值，其大小可根据实际的工程需求结合专家的指导进行设定；N—关节数量；h—时间；Q...—轨迹模型三阶导数—抖动值。

4 玻璃搬运机器人轨迹规划和优化分析

4.1 空间轨迹规划仿真分析

根据六自由度机器人关节空间三次B样条函数模型轨迹规划，编写机器人的matlab轨迹规划程序，得到末端执行器x轴方向和y轴方向的运动轨迹曲线，如图2所示。

通过对六自由度机器人关节空间三次B样条函数模型轨迹规划仿真分析，可以看出其位移曲线、速度曲线、加速度曲线均连续，但速度和加速度曲线不可导，其规划轨迹存在抖动现象。同时，该轨迹规划未直接从参量上对执行时间和抖动这两者进行权重分配，无法在机器人单次执行时间和抖动之间建立合理的平衡。为此，需要对模型进行优化，在保证机器人搬运效率的情况下降低抖动，或者在能够接受的抖动值内达到最优效率。

4.2 多目标遗传算法的机器人最优轨迹规划分析

将玻璃搬运机器人为研究对象，以建立时间-抖动最优轨迹规划数学模型，即表达式（10），进行仿真分析。为了保证优化的效果，采用实数编码方式，保证优化精度同时避免了海明悬崖问题。群体规模为100，初始的交叉概率为pc=0.7，初始的变异概率为pm=0.15，初始的精英保留策略率ps=0.05，编码因子hi的取值范围是［0.5，5］，基因的子空间为 Ω（Ω∈［0.5，5］），适应度函数，如式（11）所示。进而进行选择复制、交叉，变异采取一定的概率，对适应度高的个体进行复制，从而提高种群中的整体适应能力。每一轮进化后都会产生新的群体，采用最大代数收敛准则来判断是否结束循环。

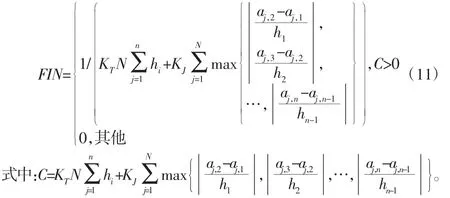
由式（11）计算可知，优化轨迹随着权重变化而变化，优化结果，如表1所示。

表1 两种权重值对应优化结果Tab.1 Two Kinds of Weight Values Correspond to the Optimization Results

表中：hi单位为 s，Jj单位为 deg.s-3。

为更进一步分析，分别对KJ/KT=0.3和KJ/KT=0.8的优化结果进行仿真分析。限于篇幅，仅列出关节1的角位移、角速度、角加速度及抖动函数关系图，如图3所示。虚线代表KJ/KT=0.3的优化结果，实线代表KJ/KT=0.8的优化结果。

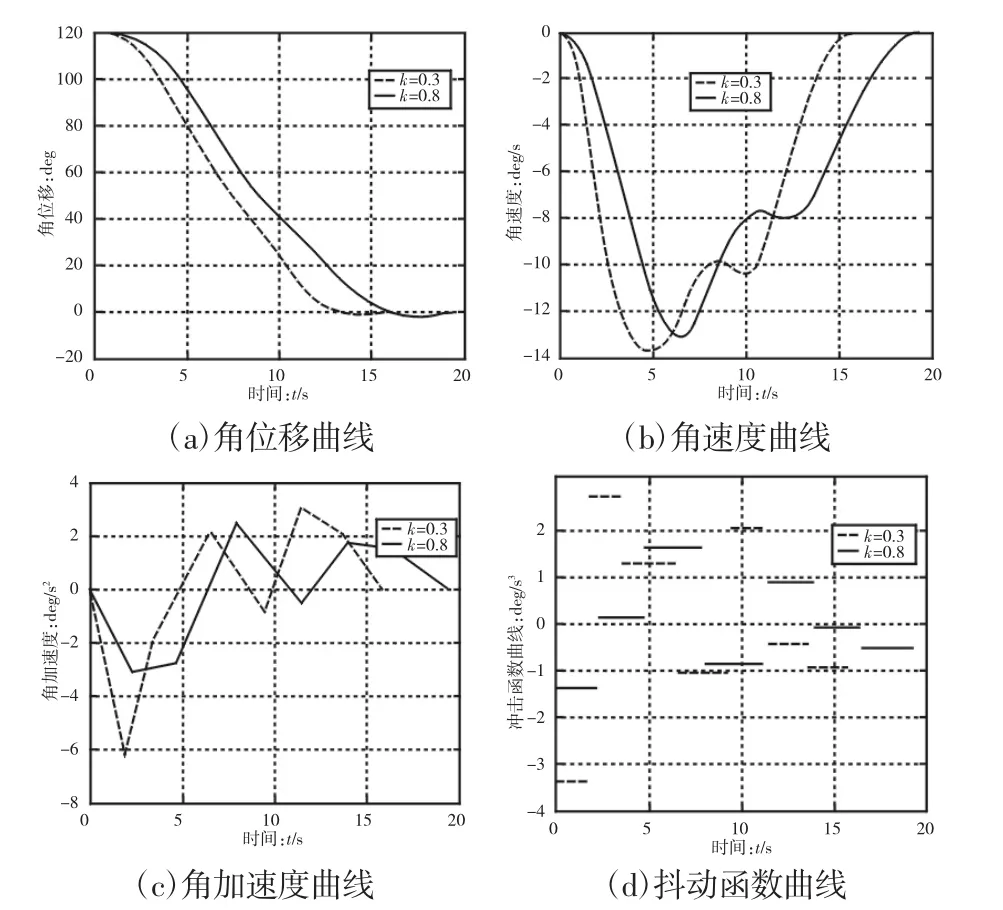
图3 玻璃搬运机器人关节1轨迹优化曲线Fig.3 The Links Optimization Curve of Trajectory of Glass Handling Robot

从图3（a）对比能发现角位移相同的情况下，KJ/KT的比值越小即时间权重KT越大时优化结果中机器人运行时间越短；从图3（b）中能看出时间权重KT越大会造成角速度峰值偏大；从图3（c）能看出时间权重KT越大加速度峰值越大，角加速度越不平滑，势必会产生更大冲击；从图3（d）能明显看出早考虑时间和抖动两个因素时，抖动权重KJ越大，抖动就会越小，优化结果中关节的运动轨迹越平滑。因此，在进行轨迹规划设定中，要根据不同玻璃的抗振动系数，设定抖动权重的前提下来对时间进行最优化设计，以满足生产过程的效率。

5 结论

（1）对六自由度机械臂进行了关节空间运动学分析，并采用三次B样条曲线对机器人进行空间轨迹规划；在B样条曲线规划基础上，建立了最优时间模型、抖动优化的数学模型，利用多目标遗传算法对模型进行了轨迹优化。

（2）经仿真分析，得到了时间权重和抖动权重对优化模型的影响程度，进一步对六自由度机器人关节空间三次B样条函数模型轨迹规划，其结果表明加速度曲线连续但不可导，存在抖动现象，为此建立了最优执行时间（也即效率）和抖动两者的平衡，使其在满足效率的前提下抖动得到有效控制。

（3）进一步，实现了基于执行时间和抖动最优对机器人进行空间轨迹规划，为玻璃搬运机器人轨迹规划提供了参考。