一种四自由度催化剂板搬运机器人研究

郑 武，邹光明，许 超，王兴东

（武汉科技大学 机械自动化学院，湖北 武汉 430081）

1 引言

随着我国经济的高速发展，环境问题受到了越来越多的关注，催化剂板作为工业脱硝中的重要催化剂材料，有着广阔的市场前景[1]。目前催化剂板搬运生产线中大多采用直角坐标系机器人，其占地面积大，运动精度相对较低；针对此问题，结合串联机构运动范围大，并联机构运动速度快、精度高的特点，许多学者对混联机构进行了研究。文献[2]设计了一种冲压混联机器人，但并未对其开展杆件参数研究。运动学是机器人研究的基础，文献[3-4]对平面五杆机构的运动学进行了研究，为这里的运动学研究提供了理论基础。为了使机器人高效、合理的完成任务，需要对其运动空间展开研究，文献[5]从雅克比矩阵行列式的值出发，分两种情况讨论了运动空间中的奇异位型问题，文献[6-8]则从避障问题出发，对运动空间展开了研究。杆件参数的确定和优化是机构设计的重要环节，Matlab二次规划函数的优化求解方法是目前主要的方法之一[9-10]，但其优化函数的建立较为困难，无法探讨各个因素对杆件参数的影响；正交试验法通过合理的选取正交因素和水平，可以直观地对比各个因素对杆件参数的影响[11]，目前在各个领域中已得到广泛应用。

针对催化剂板的搬运工作，设计了一种新的结构形式：利用平面六杆机构实现催化剂板的快速抓取；通过丝杠传动带动安装有平面六杆机构的动平台上下移动；转动座的旋转实现了动平台和平面六杆机构的水平面转动，扩大了平面六杆机构末端的水平运动范围。然后将平面六杆机构等效为平面五杆机构展开运动学研究，对其进行了正、逆运行学的推导；为了避免机构在运动中因处于奇异位型而失控，对平面五杆机构的奇异位型展开了研究，并建立了约束方程。然后通过杆件的几何关系建立起了杆件参数之间的等式，通过选取合适的正交表、正交因子和水平参数，进行了正交试验；采用极差分析和方差分析对参数影响进行了推理，确定了杆件参数。将参数带入约束方程，查看了其是否满足约束条件。最后将杆件参数带入运动学方程，运用Matlab进行编程求解，绘制了电磁吸盘的运动空间图，探讨了优化参数的合理性。

2 机器人的结构设计与运动规划

催化剂板搬运机器人结构设计，如图1所示。平面六杆机构采用对称设计，传输带、冲压机和装件箱上表面均位于同一高度；丝杠与动平台上的丝杠螺母相啮合，为动平台上下移动提供动力；导向杆有轴向定位槽，下端固接有蜗轮，定位槽与主动臂上的定位销形成配合，使其径向相对导向杆固定，轴向可动；主动臂驱动电机上的蜗杆与导向杆下端蜗轮啮合，为主动臂转动提供动力；转动座下方固接有蜗轮，通过转动座驱动电机上的蜗杆与蜗轮相啮合，带动转动座旋转。

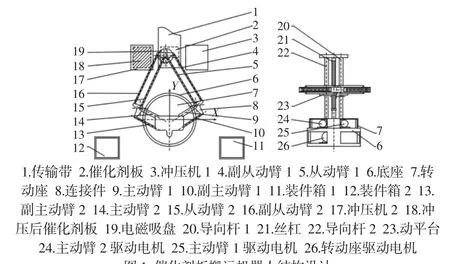
图1 催化剂板搬运机器人结构设计Fig.1 Structural Design of Catalyst Plate Handling Robot

整个搬运过程的工艺动作如下：首先，丝杠21调节动平台23，使电磁吸盘19位于传输带上表面某一合理高度。然后通过主动臂驱动电机24和25的转动，分别带动主动臂9、14的转动，使电磁吸盘19运动至传输带1上的催化剂板2正上方，抓取催化剂板。电磁吸盘19沿x轴正向平动至冲压机3正上方，放置催化剂板2于冲压机3上；电磁吸盘19沿x轴负方向平动至冲压机17正上方，抓取冲压后催化剂板18，转动座7逆时针旋转90°，使电磁吸盘19置于装件箱12正上方，将冲压后催化剂板18置于其中；转动座7顺时针旋转90°，主动臂9、14转动，使电磁吸盘19平动至传输带新运送来的催化剂板正上方，抓取催化剂板2，电磁吸盘19平动至冲压机17正上方，电磁阀关闭，将催化剂板2放置于冲压机17，主动臂9、14转动，使电磁吸盘19平动至冲压机3正上方，抓取冲压后催化剂板。最后转动座7顺时针转动90°，使电磁吸盘19位于装件箱11正上方，将冲压后催化剂板18放置于11中，转动座7逆时针转动90°，完成一个工作循环。通过合理安排机器人与传输带输送速度和冲压机冲压间隔之间的关系，对比直角坐标系机器人，可以有效的提高工作效率和精度，实现机构的精简，使占地面积大大减小。

3 机构的运动学分析

平面六杆机构与转动座连接后的结构简图，如图2所示。由图2（a）可知平面六杆机构采用对称设计，所以将两侧主动臂l1、从动臂l2分别沿x轴向坐标原点O平移l3/2距离，使其变为平面五杆机构，如图 2（b）所示。

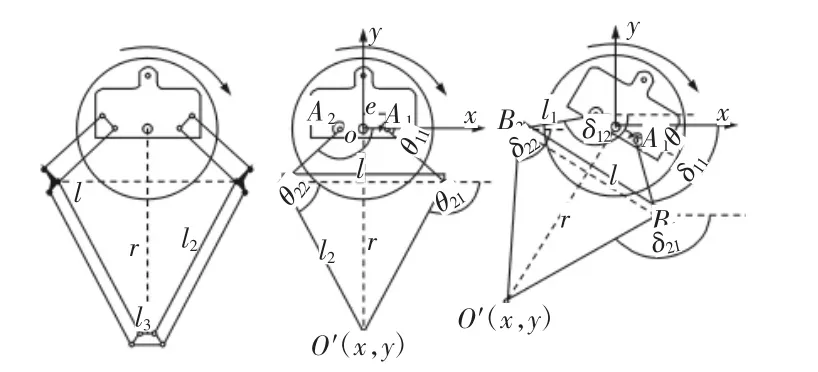
图2 平面六杆机构串联转动座结构简图Fig.2 The Structure Diagram of Plane Six-Bar Mechanism Connection Transmission Seat

3.1 运动学逆解

已知转动座关于坐标系的转动角为θ（顺时针为正），电磁吸盘O′在坐标系中的向量为r=（x，y）T，主动臂转动副距坐标原点O的距离为e。设主动臂转角为θ1i（i＝1，2），从动臂转角为θ2i（i＝1，2），则主动臂和从动臂相对于坐标系原点的转角分别为δ1i=θ1i+θ，δ2i=θ2i+θ，依据图 2（c），可以建立闭环方程：

即：r-sgn（i）ev1-l1ui=l2wi，式中：

3.2 运动学正解

机构的运动学正解是已知 θ、δ1i，（i＝1，2），求解点 O′位置矢量 r的过程。将（i=1，2）分别带入式（2），两式相减，带入 r、u1、u2、v1，得到：

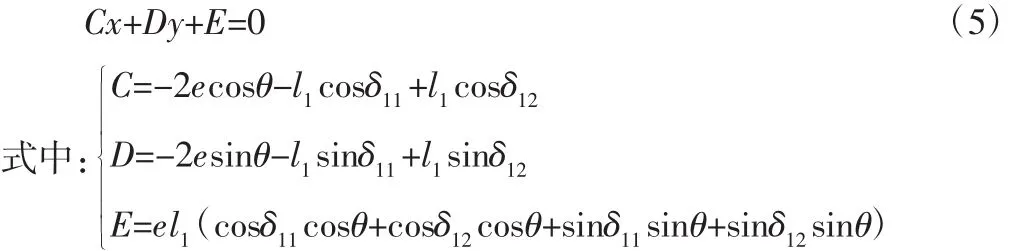
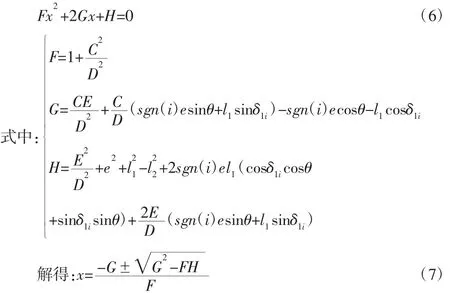
4 奇异位型和正交试验

4.1 机构的奇异位形分析

奇异位型是机器人运动过程中需要考虑的问题，当设计机构位于奇异位型的时候，就会导致其失去控制。给定右侧主动臂与x轴的上极限夹角为θ1，下极限夹角为θ2，如图3所示。此时，右侧主动臂末端端点分别为；则电磁吸盘的运动空间可表示为分别以、为圆心，右侧主动臂为半径，所画圆弧关于y轴对称所围成的封闭区域。对于平面五杆机构的奇异性问题，主要有以下两种情况：de（tJ）＝∞ 和de（tJ）→∞。

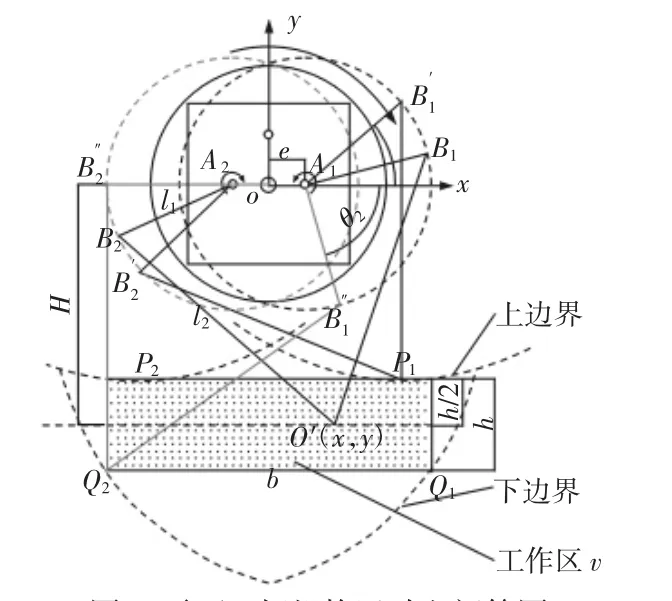
图3 平面五杆机构运动空间简图Fig.3 The Motion Space Diagram of Five-Bar Mechanism

对于de（tJ）=0，即主动臂和同侧从动臂共线。这种情况往往出现在运动空间边界，所以在运动空间中选取一个宽为b，高为h的矩形，矩形的上边界与运动空间的边界切于点P1和P2，矩形的下边界与运动空间的边界交于点Q1、Q2，给该矩形区域命名为W；其中，坐标原点距离矩形区域中心的距离为此时仅需讨论P1、P2、Q1、Q2四点处的奇异位型即可。由于平面五杆机构采用对称设计，所以 P1、Q2，P2、Q1分别为左、右两侧主动臂处于上、下极限夹角时，对应从动臂末端O′的运动轨迹与矩形边界的交点；由于机构结构对称，在此选取右侧进行讨论。由图3可知，当右侧主动臂位于上极限夹角，O′位于P1时，由于P1A1＜P1A2，所以左侧主动臂和从动臂不共线时，右侧主动臂和从动臂必不共线；为避免O′位于P1点时，左侧主动臂和从动臂共线，可采用如下约束：

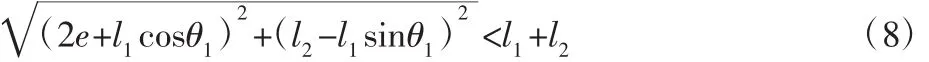
当右侧主动臂位于下极限夹角，O′位于Q2时，由于A1Q2＞A2Q2，所以右侧主动臂和从动臂不共线时，左侧必不共线；同理，为避免O′位于Q2点时，右侧主动臂和从动臂共线，可对其展开约束如下：

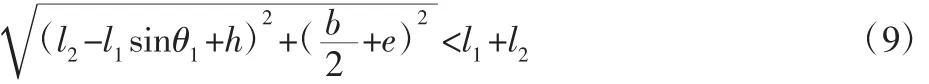
对于det（J）→∞的情形，即左右两侧从动臂共线。为防止左右两侧从动臂沿x轴水平共线，则需：

为防止左右两侧从动臂重叠共线，则需：B1B2＞0 （11）

4.2 杆件几何关系的建立及其参数选取

催化剂板尺寸为：长（300～500）mm、宽（300～350）mm、厚约0.8mm。根据结构，如图1所示。设定传输带宽400mm，冲压机宽400mm，冲压机与传输带间距100mm；所以给定工作空间W的长b=1000mm、宽h=220mm。

当已知 l1、θ1、e、θ2时，即可求出 l2。

根据设计需求，底座最小设计半径为320mm，为了保证电磁吸盘能抓到位于传输带上的催化剂板，需满足H≥320+h/2=430，即：

由图3可知，当上极限夹角θ1过大时，会导致满足工作区间W要求时，H的值过小；如若上极限夹角θ1过小，又会导致H过大，致使催化剂板相对坐标原点的力矩增大。当下极限夹角θ2的角度过大时，容易引起左右两边主动臂出现交叉或两端从动臂重叠共线的现象；而当θ2过小时，相同l1杆长，机器人末端O′的水平移动距离将大大减小。所以综合考虑，初步设θ1∈（10°，40°），θ2∈（-90°，-60°）。

机构的工作空间W与尺寸的比值为φ，其可表示为：

如果φ较大，就会对操作性能产生影响；相反，同等工作空间的情况下，φ过小，又会使机构尺寸偏大。通常取φ=（1.1～1.2），此处取φ=1.15。带入b=1000mm，得：

通过主动臂传动电机下置，假定图2（a）中l3=60mm，主动臂转动副间距最小可取240mm，则A1A2的间距最小可取为180mm，即emin=90mm。

4.3 正交试验设计

正交试验就是通过设计多个因素，带入合适正交表来进行试验，并展开分析优化的一种方法。根据等式（14）可知，l2与l1、θ1、e、θ2的取值有关，且在满足一定条件的情况下，l2的值越小越好，这样不仅可以减少制造成本，而且能减小机械手末端相对坐标原点的力矩；所以本次试验以杆长为优化目标。依据设计需求，采用三因素、三水平展开正交试验，选取L9（43）正交表，正交数据及极差分析结果，如表1所示。

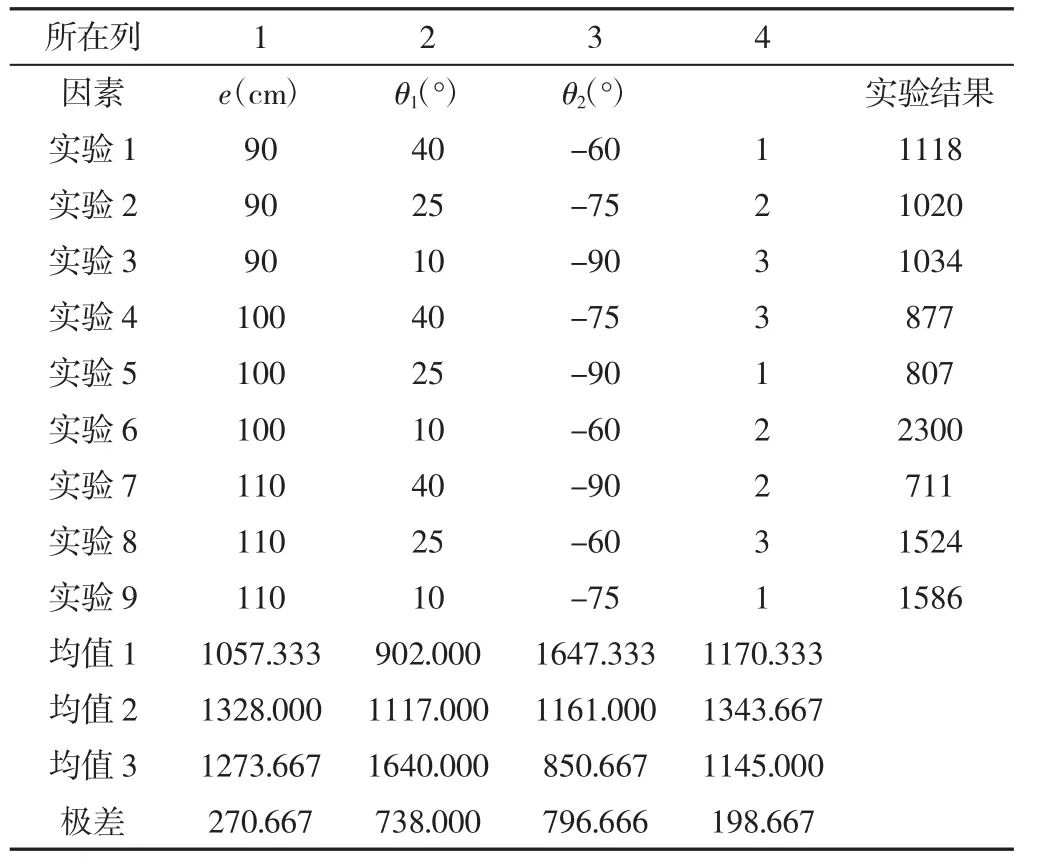
表1 正交试验表与极差分析结果Tab.1 Orthogonal Test Table and the Results of Range Analysis

由试验结果可知，下极限角θ2对杆长l2的影响最大，其次为上极限角 θ1，相对 θ1、θ2，e 对杆长 l2的影响最小。

由于极差分析不能把试验条件和试验误差所引起的数据波动区分开，不能估算出实验误差的大小；所以本次试验进一步采用了方差分析。试验中，试验数 n=9，θ1、e、θ2的水平数分别为 a=b=c=3，水平重复数分别为ka=kb=kc=3。矫正数C=T2/n=109772/9=13388281，其中T为实验结果之和。

1=2，dfb=b-1=2，dfc=c-1=2。误差自由度 dfm=dfT-dfa-dfb-dfc=2。

MSi=分别表示对应项方差，通过对比e、θ1、θ2的方差，方差值越大，代表越敏感，即可知道各参数的显著性大小。通过方差试验，可以扩大不同参数所得结果之间的差别，相对极差更有利于分析各参数对结果的影响大小。

由方卡分布可知，各个参数的方差满足方卡分布，两个方卡分布的商又恰好满足F分布，所以各参数的方差可以确定该参数对结果的影响，而误差项的方差则是参数因素以外的因素对结果造成的影响；可以用各个参数方差分别除以误差项方差，得到该参数对实验结果影响的可信度，在此用F=（SSi/dfi）/（SSm/dfm）表示。置信度α可以用于判断F分布中的比值是否在置信度以内，用F（α（dfi/dfm））表示。通常情况下，当dfm＜5时，把0.2作为临界影响值，0.1作为显著临界值。dfm＞5时，把0.1作为临界影响，0.05作为显著临界影响。由于本次正交试验dfm=2＜5，所以选取F（0.1）=9作为显著临界影响，F（0.2）=4为临界影响。方差分析表，如表2所示。

因素e各水平之和的平方和。

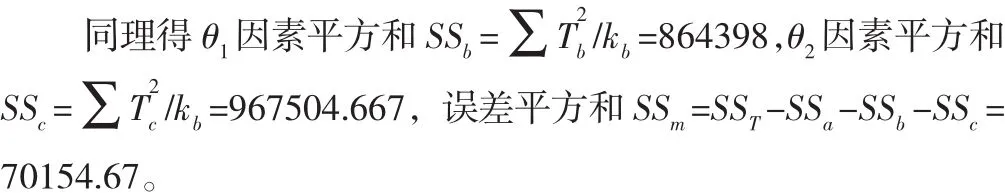
总自由度 dfT=n-1=8，e、θ1、θ2因素的自由度分别由方差分析表可知，极限角θ1、θ2均为显著性影响因数，而e几乎没有影响。这与极差分析基本一致，在此就不再做交互分析。

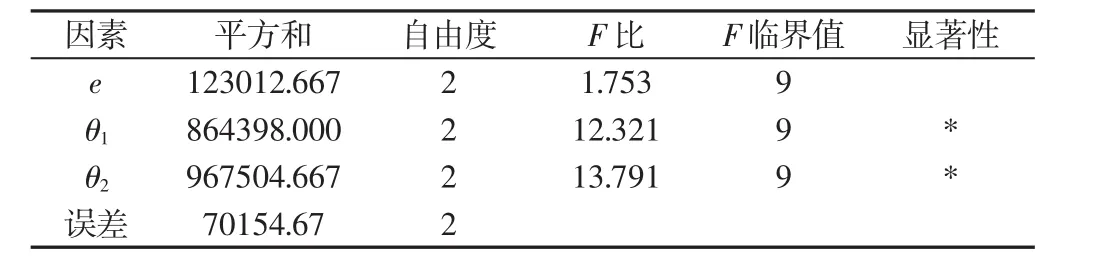
表2 方差分析表Tab.2 Variance Analysis Table

由方差分析可知，θ2因素显著影响，各因素对l2杆长影响的先后顺序为：θ2＞θ1＞e。通过对比θ2极差分析的三个均值，确定优选θ2=-90°；同理优选θ1=40°。e因素对试验结果几乎无影响，对比e各水平的极差均值，选取e1=90mm，带入等式（14），计算得l2=675mm，经对比，达到了优化的效果。将 e1=90mm、θ1=40°、θ2=-90°、l1=345mm、l2=675mm 带入约束条件（8）、（9）、（10）、（11）、（15），均满足条件，所以设计参数合理。

根据上述值，将其带入运动学方程，运用Matlab编程，对平面五杆机构O′的运动空间进行了绘制，其运动空间图，如图4所示。

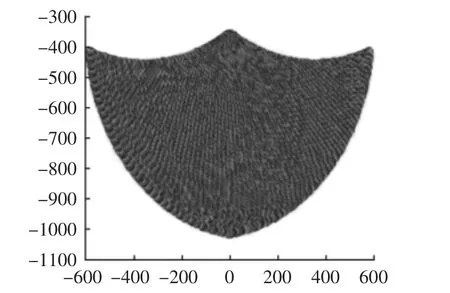
图4 平面五杆机构点运动空间图Fig.4 The Motion Space of Point of Plane Five-Bar Mechanism

通过运动空间图可知，所得的运动空间与设计空间相符，所以设计的杆件参数合理。由于转动座提供的转动副仅仅是在图4基础上让其绕坐标原点旋转；丝杠提供的移动副仅仅是在坐标系z轴上提供上下移动；在此就不再对整个机构的运动空间进行编程求解。

5 结论

（1）采用动平台带动平面六杆机构上下移动，转动座带动平面六杆机构水平转动的四自由度机器人形式，有效精简了机构的占地面积，且机械手末端运动范围大大增加。通过合理的运动路径规划，有效的提高了催化剂板的抓取装箱效率。

（2）通过对平面五杆机构的奇异位型和抓取条件展开分析，为机构的杆件参数选取建立了约束条件；然后根据运动空间需求，建立起了杆件参数之间的几何方程，并运用正交试验法中的极差分析和方差分析，求得了在满足抓取条件和约束条件下，杆件l1和l2的参数优化解。