随机模型与指数平滑模型在数据预测中的对比研究
张国发
(遵义医学院 医学信息工程学院,贵州 遵义 563006)
1 随机模型介绍
1.1 自回归移动平均模型
若时间序列yt为它的前期值和其当期与前期随机误差项的线性函数,即

则称序列yt为自回归移动平均序列,该模型为(p,q)阶自回归移动平均模型,记为ARMA(p,q)。参数φ1,φ2,…,φp为自回归系数,参数θ1,θ2,…,θp为移动平均参数,均是模型的待估参数,随机项ut为服从零均值、方差为δu2的正态分布,且互相独立的白噪声序列,成为随机误差项。而且ut与yt-1,yt-2,…,yt-p不相关;若没有θ1,θ2,…,θq部分,则称序列yt为自回归序列,该模型为p阶自回归模型,记为AR(p);若没有φ1、φ2、…φp部分,则称序列yt为移动平均序列,该模型为q阶移动平均模型,记为MA(q)。
1.2 单位根移动平均模型
若时间序列yt经过d次差分后可以使用ARMA模型来描述,则称该时间序列服从ARIMA(p,d,q),其模型为:

2 ARIMA建模步骤
2.1 数据的预处理
由于建立时间序列模型的数据要满足平稳性条件,所以对数据进行拟合预测前要对数据进行平稳化处理,可以通过时间序列的散点图或者折线图对数据序列进行初步的平稳性判断,再者可以通过自相关图的特性判断,最后再构建统计量进行辅助判断。对于非平稳的数据,我们可以采用差分的方法使其化为平稳的时间序列,但其差分的次数不宜过多,因为这样会导致模型中信息的大量丢失[1]。
2.2 模型的识别与参数估计
模型识别包含模型的类型以及相应阶数p,d,q的确定。差分阶数d的识别:如果时间序列的样本自相关系数和偏自相关系数出现衰减非常缓慢的情况,很可能是自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)过程。通常的识别是,首先计算一阶差分序列的样本自相关系数和偏自系数,对结果符合自回归滑动平均(Auto-Regressive and Moving Average,ARMA )模型的特征,则说明时间序列对于某一ARIMA(p,1,q)过程。否则,必须尝试进行高阶差分,直到产生稳定的统计特性为止。p,q确定:拖尾,p阶截尾,模型定阶为AR(p)模型;q阶截尾,拖尾,模型定阶为MA(q)模型;拖尾,拖尾,模型定阶为ARMA(p,q)模型。估计方面:本文采用ML进行估计,其优点是充分应用了每一个观察值所提供的信息,因而它的估计精度高,同时,还具有估计的一致性、渐进正态性和渐进有效性等许多优良的统计性质[2]。
2.3 模型的检验
(1)为了判断所得到的模型是否适当,还必须进行诊断检验,常用数理统计方法进行统计检验,设残差序列为e1,e2…en,H0:e1,e2…en是白噪声序列,构建统计量Q:最后利用χ2分布对时间序列模型进行诊断检验。(2)参数的检验就是要检验每个参数是否显著非零,通常应剔除不显著参数所对应的自变量并重新拟合,以构造出更精炼的拟合模型[3]。
2.4 模型的优化与预测
当一个拟合模型通过了检验,说明在一定的置信水平下,该模型能有效地拟合观察值序列的波动,但这种模型并不是唯一的,对于这种情况,我们通常采用最小信息准则(Akaike Information Criterion,AIC)和贝叶斯信息规则(Best In Class,BIC),这两个准则可以弥补根据自相关图和偏自相关图定阶的主观性,在有限的范围内,帮助我们寻找相对最优拟合模型。在经过模型识别、参数估计、模型优化后可以获得一个较为满意的时间序列预测模型。
3 模型实证分析
3.1 确定性分析:指数平滑法
首先绘制原始GDP散点图,数据选取1952—2005年期间部分GDP数据,散点图显示1990年之前增长趋势较慢,较为平稳,1990年之后数据呈现陡增趋势,与指数增长方式相似,又由于一次和二次指数平滑得到的预测值都要明显滞后于实际值,这样就会产生较大的误差。综上分析,我们选用三次平滑法比较具有合理性。
指数平滑法的预测模型为Ft+1=ayt+(1-a)Ft,其中:yt—第t期的实际值;Ft—第t的预测值;a—平滑系数,在Excel中,它称为阻尼系数。由于我们采用三次指数平滑法,则用二次曲线预测模型Ft+m=at+btm+ctm2。
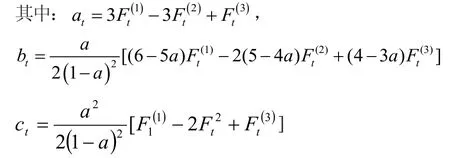
原数列波动较大a宜取大值,即0.6~0.8,这样可以加重近期观察值的权重,使各期观察值的权重由近到远较快地变小,分别取a=0.8,a=0.7,a=0.6做指数平滑,取a=0.6,标准误差比较小,所以我们选择a=0.6作为模型预测的标准,2005年的=154 783.6,=131 248.3=112 389.4,经计算:
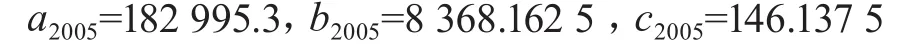
预测方程为:
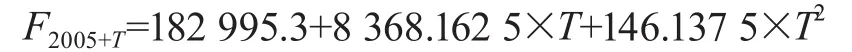
当T=1时,2006年的预测值为:F2006=191 509.6
当T=2时,2007年的预测值为:F2007=200 316.2
当T=3时,2008年的预测值为:F2008=209 415
GDP预测数据比较如表1所示。
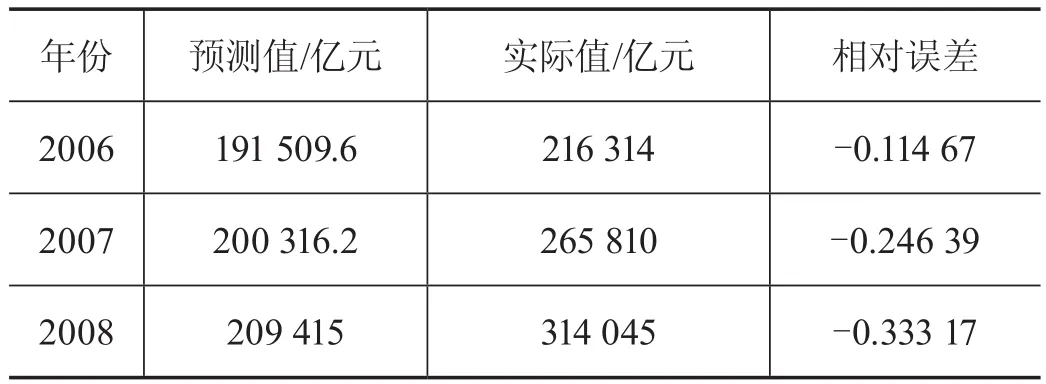
表1 GDP预测数据比较
3.2 随机性分析:平稳性检验与纯随机性检验
经图形法检验,1952—2005年历年GDP数据具有明显的上升趋势,因此此时间序列是非平稳序列,同时,经自相关系数图检验,自相关系数缓慢衰减,同样说明序列存在一定的非平稳性;如果序列是平稳的,也不一定都值得建模,只有那些序列值之间具有密切的相依性,历史数据对未来的发展有一定的影响,才值得我们花时间去挖掘历史数据中的有效信息,以便用来预测序列未来发展,经自相关函数悬针图检验,显示没有一个样本自相关系数严格等于零,但这些自相关系数比较大,都以一定的幅度做着波动,由此可知不是白噪声序列,同样,由白噪声检验可知,可知LB(6)=154.93,LB(12)=179.30,LB(18)=179.97,LB(24)=186.40,其p值都小于0.05;显著表明该序列不是白噪声序列,这完全符合事实。
3.3 建模处理
(1)观察图形后,发现图形成指数上升形式,变化浮动比较大,表明其数据存在异方差,故作对数变换;经对数变换后可以看出它有明显的线性增长趋势,对序列做初步识别。
(2)观察取对数后的样本自相关系数,呈现缓慢下降的趋势,判断该序列是非平稳的。
(3)结合观察,我们知道要对序列作差分运算,作一阶差分,再观察差分后样本自相关系数和偏自相关系数图;经检验在显著性水平为0.01的条件下,由于各阶延迟下χ2检验统计量的p值显著小于0.01,我们有很大把握(置信水平>99%)断定序列属于非白噪声序列。
(4)对对数差分后的平稳非白噪声序列进行拟合ARMA模型。可以得到对数差分后序列的自相关系数很快衰减到0,具有1阶不截尾的性质,而偏自相关也显示出1阶不截尾的性质,分别到6阶才出现截尾,初步确定为ARMA(6,6),为了检验所选择的模型是否合适,对模型进行最优识别,经计算可知p=2,q=0时BIC(2,0)=-6.006 74最小,因此模型ARMA(2,0)最优,故我们选择ARIMA(2,1,0)模型。
(5)模型估计和显著性检验:经模型拟合优度检验,所有系数估计全部通过检验,模型可以表示为:化简为y-y=0.112 25+0.594 3tt-1(yt-1-yt-2)+εt,则最终拟合模型为:yt=0.112 25+1.594 3yt-1-0.594 3yt-2+εt,对该模型进行残差检验,残差是白噪声序列,该模型适应。
(6)进行预测,预测大陆地区未来3年的每年国民生产总值。GDP预测数据比较如表2所示。
4 结语
由比较结果可以看出第二种方法的预测值与实际值最为接近,即该种方法最好,故最后选取第二种方法对未来3年的GDP做出预测。从文中分别采取确定性分析和随机性分析的方法对时间序列做出分析和预测的结果可以看出,随机性ARIMA模型的分析结果要好于确定性分析的指数模型,由于对于非平稳的数据可以采用差分处理,但差分的次数不宜过多[4-5]。本文采用一次差分较为合理,同时又采用对数相结合的方法,取得了较为满意的预测结果,为进行类似数据的预报提供了一个参考依据。

