平行板和圆柱形电容器电容表达式推导及应用

陈乐坤

1.研究背景

电容器是一种容纳电荷的器件，它可以由两个彼此绝缘且相隔很近的导体构成，是电子设备中大量使用的电子元件之一[1]。随着电子信息技术的日新月异，数码电子产品的更新换代速度越来越快，带动了电容器产业增长。当前，电容器最前沿的研究对象为超级电容器[2]。本文基于高斯定律，利用微积分知识，重点针对圆柱形电容器的电容公式推导及应用展开了研究，为电容器的发展起到了积极的推动作用。

2.电通量及计算

电通量（符号：ΦE）是电场的通量，与穿过一个曲面的电场线的数目成正比，是表征电场分布情况的物理量。电通量它是标量。

2.1 匀强电场中平面的电通量

匀强电场下平面的电通量计算是复杂电场下曲面电通量计算的基础，因此我们首先来讨论匀强电场下平面电通量的计算。考虑如下物理模型：一个大小为S的长方形放置在一个电场强度大小为E的电场中，且长方形与电场强度（电力线）相垂直。根据电通量定义可得：

当电场强度的方向与平面的法向量方向呈夹角θ时，将电场强度进行正交分解，分解成与平面垂直的矢量分量和与平面平行的矢量分量。由电通量定义可知，与平面平行的电场强度矢量分量在S平面上的电通量为0，则有：

2.2 非匀强电场中曲面的电通量

对于非匀强电场下曲面电通量的计算，采用的是微积分的思想，将计算区域划分成无限多个微元面，首先计算每个微元面的电通量，然后进行叠加得到整个区域的电通量，其具体过程为：首先将曲面S划分为若干个微小的面元dS，在每个面元区间内，电场可近似为匀强电场，即电场强度E的大小和方向基本不变，且微元面可近似为一个多边形（小平面）。此时，对于每个微面元，它的电通量计算就等效为匀强电场下平面电通量的计算，可根据公式(2)计算得到公式(3)，其中θ为微元面的法向量与穿过它的电场线的夹角。

由于整个曲面S的电通量就近似等于所有微面元电通量之和，用公式表示为：

当对曲面划分的微元面无限小的时候，公式(4)即为该曲面电通量的准确表达式，用微积分形式表达可得：

公式(5)即为求解任意曲面电通量的一般表达式。

3.高斯定理

高斯定理表述为：在静电场中，穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷的代数和有关，且等于封闭曲面的电荷的代数和除以真空中的电容率。下面以点电荷激发的电场为例，对高斯定理进行证明。

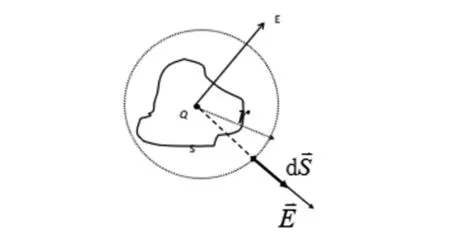
图1 高斯定理证明过程

如图1所示，在空间中存在任意形状的闭合曲面S，闭合曲面内包含了一个点电荷Q，此时以点电荷Q为球心做一个半径为r的闭合球面S2，且球面完全包含曲面S。根据电力线的连续性定理，穿过曲面S的电力线数目与穿过球面S2的电力线数目相等。由电通量的定义可知：电通量与穿过一个曲面的电场线的数目成正比，因此，曲面S的电通量与球面S2的电通量相等。则求解包含点电荷的任意曲面s的电通量就转换为求解以该点电荷为球心的球面的电通量。

根据公式(5)可知，穿过闭合球面的电通量为：

已知电场强度计算公式(7)如下所示：

由此可知，电场强度的大小由电荷量和距点电荷的距离决定，由于闭合球面上的点到点电荷（球心）的距离处处相等，因此球面上的电场强度大小处处相等，将公式(6)和(7)联立可得：

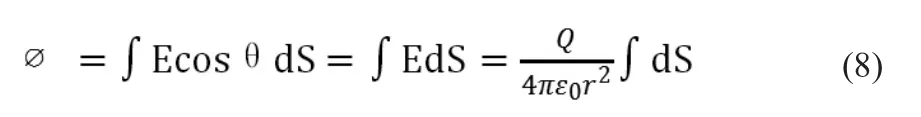
结合球表面积计算公式，最终可得：

由此可知，任意一个包含点电荷的闭合曲面，它的电通量就等于该点电荷所带电量除以真空电导率。

当点电荷在任意闭合曲面（高斯面）之外时，证明的原理仍然基于电力线的连续性定理。其基本过程为：以点电荷为球心，以高斯面所覆盖的立体角φ为区域，绘制规则的闭合面，它由两个规则的球面（立体角均为φ）围成，且两球面之间的距离dr无限接近于零，则穿过这两个规则球面相同位置的电通量大小相等方向相反，叠加之后为零，因此点电荷在高斯面之外时，穿过该高斯面的电通量为零。

根据以上推导过程即可得到高斯定理，推而广之，在任意介质中，一个高斯面的电通量就等于它所包含的所有点电荷带电量的代数和除以该高斯面所在介质的介电常量，如公式(10)所示。

4.电容器电容表达式推导

电容器表达式的推导可以遵从以下几个步骤：（1）依据电场强度分布特点构建高斯面[3]-[4]，计算高斯面的电通量；（2）利用高斯定理得到电容器电场强度与极板电荷量之间的关系；（3）计算电场强度；（4）计算两极板之间的电势差U；（5）通过电容C定义式计算电容量。下面对平行板电容器和圆柱形电容器电容分别进行推导，物理模型如图2所示。

图2 平行板和圆柱形电容器高斯面

4.1 平行板电容器表达式推导

平行板电容器如图2(a)所示，由于电平行板电容器极板间电场强度为匀强电场，电力线只存在与两极板之间，由正极板出发垂直到达负极板（忽略极板的边缘效应），因此将高斯面构建成一个闭合的长方体，如图2(a)所示，该长方体包裹着其中一个极板，且长方体的侧面与极板平行。当长方体的某一表面与电力线平行时，穿过该表面的电通量为零，则根据电通量定义及公式(5)可得：

其中E为极板间的匀强电场大小，S为两极板的正对面积。结合高斯定理及公式(10)可得：

其中ε为极板间的材料介电常量。由于平行板电容器板间电压与电场强度服从公式(13)，结合公式(12)和(13)，及电容C定义式最终可得公式(14)：

其中εr为材料的相对介电常数，k为静电力常量，d为两极板间距。

4.2 圆柱形电容器表达式推导

圆柱形电容器电容表达式的推导与平行板电容器的表达式推导方法一致，其中最关键的是高斯面的建立。分析圆柱形电容器电场分布特点可知：它的电场呈轴对称型分布，电力线由正极板指向负极板，方向沿圆柱筒的径向，而轴向上没有电力线，因此建立圆柱形电容器的高斯面如图2(b)所示，此时高斯面上下底面与电力线平行，它们的电通量为零，只有侧面的电通量不为零。若记圆柱筒轴向上单位长度极板所带电量为λ，则根据公式(5)和(10)可得：

根据电势差的物理含义：AB两点之间的电势差等于电场中在电场力的作用下单位电荷由A点移动到B点电场力所做的功，可得：

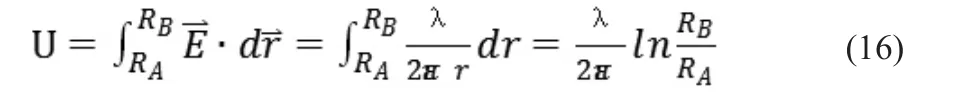
其中r为高斯面的半径，RB和RA为圆柱形电容器外半径和内半径。再由电容定义式，最终得到圆柱形电容器的电容表达式为：

其中L为圆柱形电容器长度。

5.电容特性及应用

通过分析平行板电容器与圆柱形电容器的电容表达式，可得到如下结论：

（1）电容值的大小与极板间填充材料介电常数成正比；

（2）电容值的大小随着两极板间距的增加而减小；

（3）电容值的大小随着两极板正对面积的增加而增加；

（4）电容值的大小与存储的电量、外加电场均不相关；

（5）电容是电容器的固有属性由此，可以利用电容器测量某些物理量，其核心思想为：将该物理量与电容的三个关键参量（板间距、极板正对面积和板间材料介电常量）中的某个或多个关联起来，通过测量电容量（电容的改变量）来获取某物理量的大小，例如：利用圆柱形电容器测量汽车油箱剩余油量，通过测量电容的改变量推导出容器液面高度，进而确定剩余的油量[5]。

6.总结

电容器是电子设备中大量使用的电子元件之一。本文针对平行板和圆柱形电容器的电容计算及应用展开了深入研究。首先研究了电通量的物理含义及计算方法，然后对高斯定理进行了理论证明和物理含义解析，在此基础上结合微积分知识对电容器的电容表达式进行了推导，并探讨了电容量作为电容器固有属性所表现出来的特性。基于以上研究，最终给出了利用电容器测量油箱剩余油量等物理量的方法，为电容器的发展起到了积极的推动作用。