匈牙利算法在指派问题中的运用
钟莉梦桃,易磊,葛巍,欧懿坤
(西南科技大学经济管理学院,四川绵阳621010)
引言
随着现代化先进科学技术的发展,先进的生产设施、科学的管理思想等使得生产运作系统功能不断完善,企业生产运作效率不断提高。与此同时人员成本颇高仍是限制企业高效、常稳发展的一块短板。如何在已有经验数据的基础上对企业人员进行更高效合理的配置是减小人力成本的一有效举措。
1 指派问题
指派问题,其目的是安排m个人完成n项任务并使总效率达到最高(即所需总时间最少),也称为分配或配置问题,是关于资源合理配置或最优配置的问题。
2 匈牙利算法简介
匈牙利算法,是基于效率矩阵每一行元素减去该行位势,每一列元素减去该列位势后得到的新效率矩阵和原效率矩阵最优解相同,以及矩阵A中覆盖所有0元素的最少直线数等于位于不同行不同列的零元素(即独立元素)的最大个数这两个定理来解指派问题的计算方法。其具有三个运算前提:目标函数求最小值、人数m与任务数n相等以及效率非负。
匈牙利算法的步骤:
2.1 建立资源配置方案的效率矩阵,并转换为匈牙利算法所要求的标准型d×d阶矩阵B,其中d=max(n,m)。当人数m 小于任务数n时,增加虚拟人员行,当任务数n小于人数m时,增加虚拟任务列。
2.2 分别找出当前效率矩阵中每行每列的最小元素,并分别从每行、每列中减去该元素,形成新效率矩阵。
2.3 用最少直线数k覆盖所有零元素。
2.4 当k=d时停止运算,得到最优配置方案,当k≠d时,从矩阵未被覆盖的数字中找到最小数值s,未被覆盖的元素减去s,直线相交处元素加上s,被直线覆盖而没有相交的元素不变,得到新效率矩阵C1。
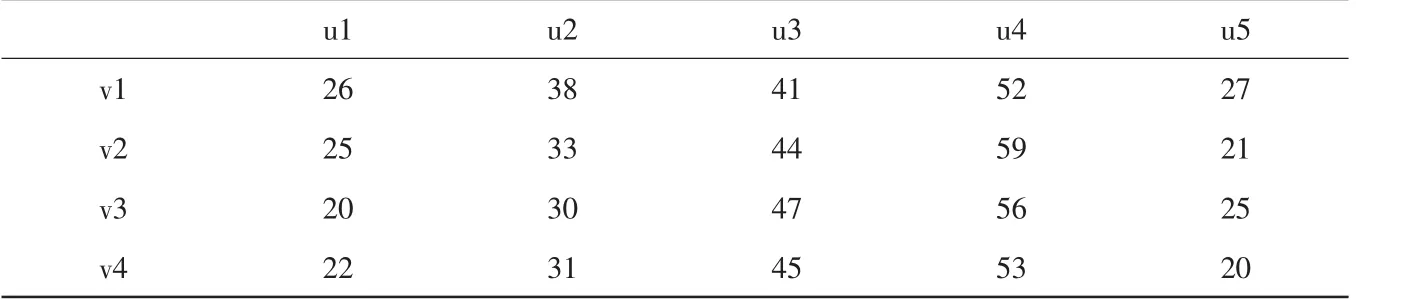
表1.1效率表
2.5 重复以上步骤2、3,直至k=d。
3 匈牙利算法在具体指派中的运用
现要求四个人(v1、v2、v3、v4)完成五项任务(u1、u2、u3、u4、u5),其中某人将完成两项,四人各自完成五项工作的效率如表1.1所示。
运用匈牙利完后五项任务分配的指派问题具体步骤如下:
3.1 建立标准化效率矩阵B1。增加人员v5行,其对应五项任务的矩阵分别为0(其他四人的效率最小值)。

3.2 找出当前效率矩阵中每行的最小元素,并从每行中减去该元素,形成新效率矩阵B2。找出效率矩阵B2中每列的最小元素,并从每列中减去该元素,形成新效率矩阵B3。

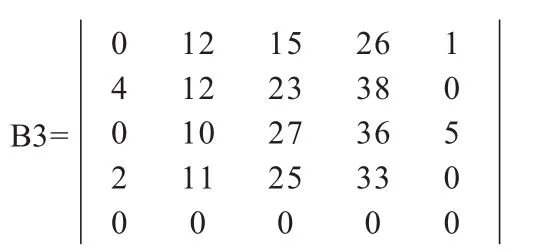
由以上最终指派矩阵E得出结论:人员v1完成任务u3,u4,(E中显示虚拟人员v5完成任务u4,此时由完成任务u4效率最高的v1完成),人员v2完成任务u5,人员v3完成任务u1,人员v4完成任务u2。
4 结语
提高人员工作效率降低人力资源成本是企业不断消除浪费、降低成本,积极进取的经营思想,是企业的求生之路。而资源的优化配置正是企业提高生产运作管理系统,以减少企业成本增加消费者剩余的一种有效途径。本文结合实际案例,运用运筹学中求解指派问题的匈牙利法建立指派问题模型并求得效率在理想状况下的最优解,验证了匈牙利法在求解实际人员分配方案的可行性。

