偏摆式平面研磨抛光轨迹的理论研究*
严 振, 方从富, 刘 冲
(华侨大学 机电及自动化学院, 福建 厦门 361021)
随着半导体产业的快速发展,人们对碳化硅、蓝宝石等半导体产品表面质量和面形精度的要求更高,需要不断克服其加工技术难题来满足该产业未来的发展需要。而研磨抛光技术作为一种精密、超精密加工手段,在该领域起到了举足轻重的作用,特别是近来研究比较热门的固结磨料研磨抛光加工技术[1]。由于固结磨料加工中磨粒是固结在工具表面的,磨粒与工件间的干涉路径仅与研磨抛光运动形式和磨盘表面图案结构有关。磨粒与工件间的干涉路径通常采用磨粒运动轨迹进行表征,而研究发现磨粒运动轨迹的非均匀性与研磨抛光过程中材料去除的非均匀性直接相关[2]。因此,研究磨粒运动轨迹的非均匀性对提升材料去除的均匀性具有重要的意义,这对优化研磨抛光加工工艺参数和磨盘表面图案结构等均具有重要的理论和实用价值。
为了获得表面高质量的工件,国内外学者在磨粒运动轨迹非均匀性方面做了大量的研究[2-11]。研究表明:磨粒运动轨迹的非均匀性与材料去除非均匀性具有紧密的内在联系,低的磨粒运动轨迹非均匀性能够获得更好的材料去除均匀性。学者在这方面的研究主要针对的是定偏心式和行星式研磨抛光等运动形式,研究其转速比、偏心距等对磨粒运动轨迹的影响。随着自动化程度的不断提高,偏摆式等不定偏心研磨抛光运动也逐渐引起人们的重视。该种研磨抛光运动具有协调工件表面磨粒运动轨迹分布的优点,能够获得更高的工件表面质量,而有关偏摆式研磨抛光轨迹方面的研究还十分欠缺。因此,为了提高加工质量和加工效率,十分有必要研究偏摆式磨粒运动轨迹形态及其非均匀性特征。
我们通过引入正弦直线偏摆运动,推导了包容定偏心的偏摆式磨粒运动轨迹方程;从大量磨粒表征磨盘特征入手,以磨粒运动轨迹非均匀性为评价指标,重点研究了转速比、偏摆幅度、偏摆角度以及偏摆角速度对磨粒运动轨迹非均匀性的影响。这对理解研磨抛光工艺参数对加工过程的影响,具有重要的现实意义。
1 轨迹建模与评价
研磨抛光加工过程如图1所示,研磨盘以角速度ω1绕其中心轴转动,载物盘以角速度ω2绕其中心轴转动,工件紧贴在载物盘底部,通过对载物盘施加一定的压力,实现固结磨粒研磨盘对工件的研磨加工。当工件中心相对研磨盘中心轴的位置不变时,为定偏心加工方式;当工件中心相对研磨盘中心轴的位置随时间做周期性的不定偏心运动时,为偏摆式加工方式。本研究的偏摆方式为正弦波动形式的正弦直线摆动。

图1 研磨抛光加工过程
1.1 轨迹建模
为便于对研磨抛光过程进行运动学分析,将其简化为图2所示的模型。分别以研磨盘和工件中心为坐标轴中心建立直角坐标系XOY和xoy,中心分别为O和o。研磨盘旋转角速度ω1,工件随着载物盘的旋转角速度ω2,研磨盘的半径R,工件的半径r。
当加工方式为偏摆式加工时,工件运动为复合式运动,工件除回转运动外,还附加了一个沿研磨盘的直线正弦式摆动。设定工件在初始位置时的偏心距为e,偏摆幅度为q,偏摆角速度为ω3,摆动方向与X轴所成的夹角β为偏摆角度。则,在XOY坐标系下工件中心点的坐标随时间t的变化可以表示为:
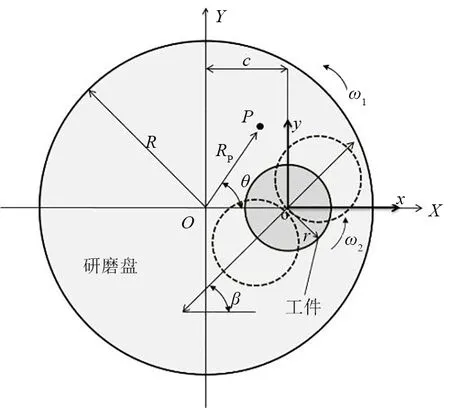
图2 运动模型平面示意图
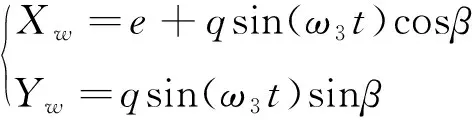
(1)
通过对单颗磨粒相对工件运动的轨迹分析,令研磨盘上任一点P离坐标O点的距离为Rp,初始角为θ,则磨粒点P(Rp,θ)在XOY坐标系下的运动轨迹方程为:
(2)
基于坐标系XOY和xoy,运用运动学知识,可以得到2坐标系的转换关系为:
(3)
然后,通过变换推导,研磨轨迹在xoy坐标系下的关系式为:
(4)
根据式(1)和(4),可得偏摆运动下磨盘上任一点P相对工件的运动轨迹方程为:
(5)
根据建立的单颗磨粒运动轨迹方程,可以分析大量磨粒共同作用下的研磨轨迹分布。基于此,我们构造如图3所示的磨块式研磨盘,磨块在研磨盘上呈同心环均匀分布。磨块的个数为54,磨块的半径为10 mm,每个磨块上均匀分布17颗磨粒。
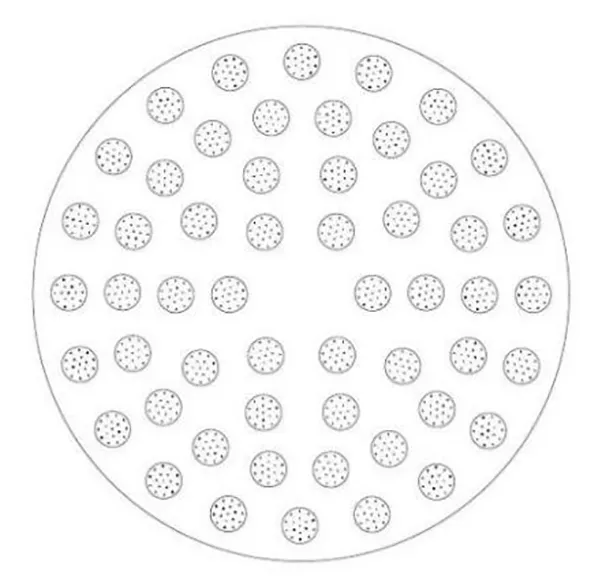
图3 磨块式研磨盘示意图
1.2 轨迹评价
采用轨迹非均匀性方法定量评价研磨轨迹分布[4]。该方法是通过工件表面网格化来统计工件表面不同位置区域磨粒划擦工件的次数,基于统计的轨迹路径次数,计算轨迹非均匀性系数值。若非均匀性系数越小,则表明轨迹的均匀性越好。根据文献[7],设定网格大小为1 mm×1 mm,时间步长为0.001 s,则轨迹非均匀性系数NUT可表示为:
(6)
式(6)中:n为网格的总数量,N(i)为第i个网格中磨粒划擦次数,m为所有网格划擦次数的平均值。
2 轨迹分析
设研磨盘半径R=150 mm,工件半径r=50 mm,工件旋转角速度ω2=2π rad/s,仿真时间t=60 s。研究偏心距和偏摆运动参数(偏摆幅度、偏摆角度、偏摆角速度)对轨迹非均匀性的影响,并通过单颗磨粒轨迹分布进行佐证。
2.1 偏心距的影响
考虑到磨粒分布和工件-磨盘相对运动的影响,偏心距(工件中心位置)的改变必然导致研磨轨迹发生变化。首先考虑偏心距的变化对轨迹非均匀性的影响。根据设定的磨盘和工件尺寸,选取偏心距e为70、75、80、85、90、95、100、105 mm。根据以往的研究结果[12-13],取研磨盘与工件的转速比n=1.11。研究的对象是定偏心方式,不考虑偏摆运动,即偏摆幅度为0的情况。通过MATLAB模拟仿真不同偏心距下的轨迹非均匀性结果如图4所示。
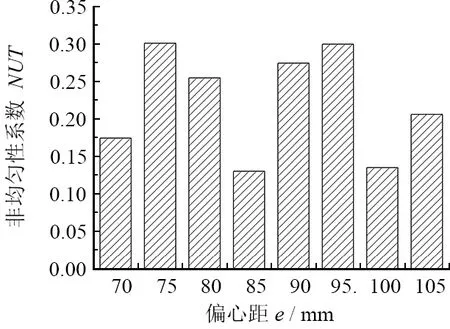
图4 不同偏心距对轨迹非均匀性的影响
从图4中可以看出:不同偏心距下的轨迹非均匀性系数值差异很大,即随着偏心距的增大,轨迹非均匀性系数呈现波动变化。当偏心距为85 mm和100 mm时,轨迹非均匀性系数相对较小,约为0.140。这说明偏心距过大或过小,都将导致研磨轨迹分布差异变大,致使轨迹非均匀性系数增加。基于仿真计算的结果,可以对实际加工过程进行理论指导,选择合适的偏心距有利于提高加工质量。
2.2 偏摆运动的影响
偏摆运动对轨迹非均匀性影响的因素有偏摆幅度q、偏摆角度β和偏摆角速度ω3,故从这3个参数展开研究。首先确定工件初始位置,为了不失一般性,根据上述对偏心距的分析,选择2个对非均匀性差异影响较大的偏心距,考虑到要求工件位于相对研磨盘半径方向相对中心的位置,观察图4,分别选取e为85 mm和90 mm作为偏摆中心进行研究。
2.2.1 偏摆幅度
为了研究偏摆幅度对轨迹非均匀性的影响,取偏摆角速度ω3=1 rad/s,偏摆角度为0°(摆动方向为水平方向),转速比n=1.11。其他参数固定不变,偏摆幅度q取5、10、15、20、25 mm。图5为水平偏摆时不同偏摆幅度对轨迹非均匀性的影响,图5中,偏摆幅度为0表示未加偏摆运动的情况。图5的结果表明:引入偏摆运动后,不同偏摆幅度对轨迹非均匀性有显著改善。随着偏摆幅度的增加,轨迹非均匀性系数先逐渐减小;但当幅度过大,工件露出磨盘部分面积越大,轨迹非均匀性系数有增大趋势。2种偏心距下的结果表明:在偏摆幅度为15 mm左右时,都可以达到一个相对较小的轨迹非均匀性,轨迹非均匀性值可减小到0.060左右,且2个值很接近。这说明引入偏摆运动可以协调不同偏心距下的轨迹分布,使轨迹分布非均匀性系数降低。通过优选偏摆幅度,可获得更低的轨迹非均匀性值。
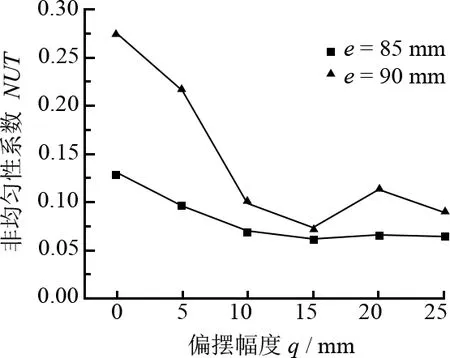
图5 不同偏摆幅度对轨迹非均匀性影响
2.2.2 偏摆角度
为了研究偏摆角度对轨迹非均匀性的影响,根据上述研究,取偏摆幅度q为15 mm,偏摆角速度ω3=1 rad/s,转速比n=1.11。固定其他参数,偏摆角度β取0°、15°、30°、45°、60°、75°和90°。图6是2种偏心距下偏摆角度变化对轨迹非均匀性的影响图。从图6可以看出:2种偏心距下,偏摆角度对轨迹均匀性的影响具有很好的一致性。在0°~30°范围内,轨迹非均匀性系数略微下降,变化不明显,尤其在30°附近时,轨迹非均匀性系数最小,其值可达0.058;而在30°之后,随着偏摆角度的增大,轨迹非均匀系数越来越大;当偏摆角度为90°时,即垂直摆动时,轨迹非均匀性系数基本与未加偏摆时相同。
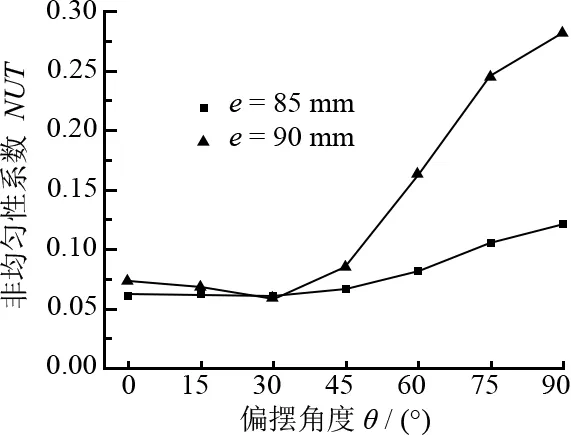
图6 不同偏摆角度对轨迹非均匀性影响
2.2.3 偏摆角速度
为了研究偏摆角速度对轨迹非均匀性的影响,取偏摆角度为30°,偏摆幅度为15 mm,转速比n=1.11。分析正弦偏摆角速度的影响时,选取普通偏摆角速度为0.5、1.0、1.5、2.0、5.0、10.0 rad/s和特殊π倍偏摆角速度π、2π、3π、4π rad/s,选定的范围较大,以便发现其一般性规律。图7为2种偏心距下不同偏摆角速度对轨迹非均匀性的影响。从图7a可以看出:普通偏摆角速度的变化基本不影响轨迹非均匀性,且轨迹非均匀性系数较小。分析图7b可以发现:轨迹非均匀性系数都较大,甚至高于未加偏摆运动的轨迹非均匀性系数。分析其原因可能是偏摆运动的周期性与工件旋转的周期性存在一定的比例关系,使得磨粒与工件之间的干涉减弱,从而使轨迹非均匀性反而变差,而偏摆角速度取其他值时则不存在这种情况。为了验证这种猜想,下面作进一步的分析。
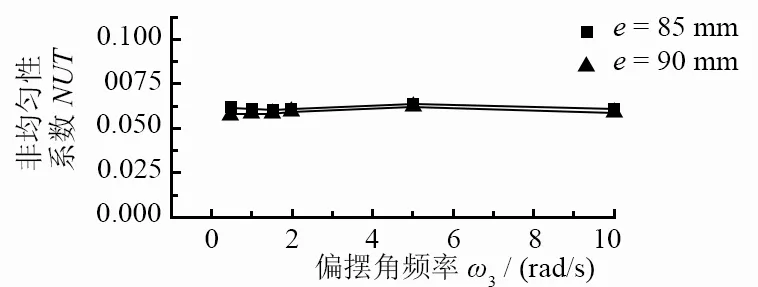
(a)普通偏摆角速度
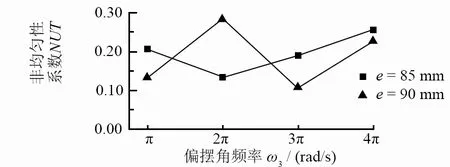
(b)特殊π倍偏摆角速度
设偏摆角速度ω3与旋转角速度ω2之比为k,取旋转角速度的值为4 rad/s和6 rad/s,其他条件不变,得到不同k值对轨迹非均匀性的影响如图8所示。
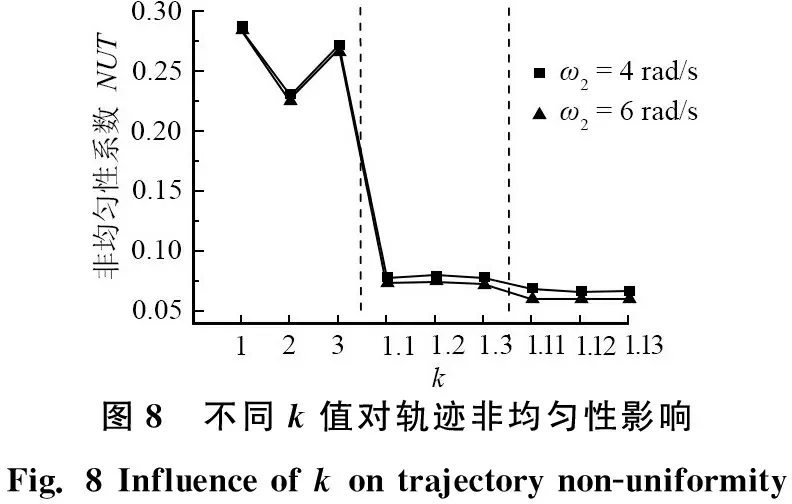
图8 不同k值对轨迹非均匀性影响Fig. 8 Influence of k on trajectory non-uniformity
从图8中可以看出:当k取整数值时,轨迹非均匀性很差,其值可高达0.284;当k取小数时且小数位越多,非均匀性越好,这与转速比对轨迹非均匀性的影响规律相一致。
2.3 单颗磨粒轨迹分布特征
通过观察单颗磨粒轨迹分布图,分析加偏摆运动与不加偏摆运动以及加偏摆在不同转速比和k值下的磨粒运动轨迹形态,取偏心距e=85 mm,磨粒径向位置Rp=70 mm,磨粒初始角度θ=0°,转速比n=1、1.1和1.11。在加偏摆情况下,偏摆幅度q=20 mm,偏摆角速度ω3=1 rad/s,偏摆时考察偏摆角度为0°、30°和90°,k值取1和2,仿真时间t=60 s。图9为不同偏摆情况及不同转速比下的磨粒轨迹分布图,图中粗圆圈区域代表工件。
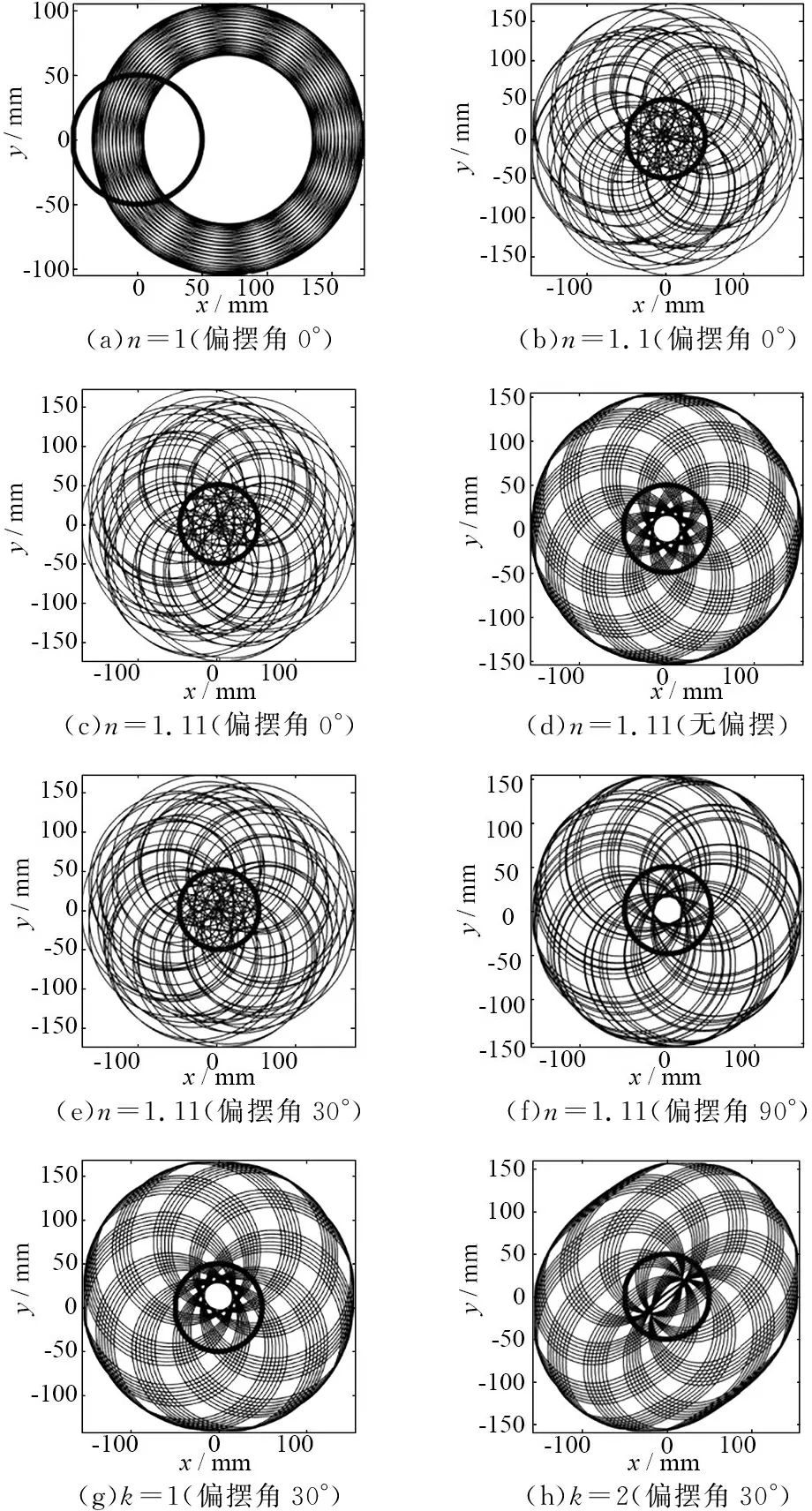
(a)n=1(偏摆角0°)(b)n=1.1(偏摆角0°)(c)n=1.11(偏摆角0°)(d)n=1.11(无偏摆)(e)n=1.11(偏摆角30°)(f)n=1.11(偏摆角90°)(g)k=1(偏摆角30°) (h)k=2(偏摆角30°)
图9不同参数下的磨粒轨迹图
Fig.9Abrasivetrajectorymapsunderdifferentparameters
图9a、9b、9c为在不同转速比下偏摆角度为0°时的轨迹分布图;图9d、9e、9f为转速比为1.11下未加偏摆以及偏摆角度为30°和90°时的轨迹分布图;图9g、9h为比值k取不同整数时的轨迹分布图。
从图9可以看出:转速比为小数时的轨迹分布均匀性较好;与未加偏摆的磨粒轨迹图相比,在偏摆角度为0°和30°时,工件区域轨迹分布更趋于复杂化和均匀化;并且,在这2种偏摆角度下的磨粒轨迹图区别很小,这与上面分析的2种角度下的非均匀性差异不大的结果能够很好地吻合。当偏摆角度为90°时,轨迹重合度较高,甚至高于未加偏摆运动的情况,导致轨迹非均匀性较差。比值k取整数时,其轨迹分布与未加偏摆的轨迹分布只发生略微变化,验证了k取整数时轨迹非均匀性变差的结论。
3 结论
基于偏摆式平面研磨抛光轨迹模型和轨迹非均匀性评价指标,利用MATLAB软件,系统分析了偏心距、偏摆幅度、偏摆角度、偏摆角速度等对轨迹非均匀性的影响规律,结合不同偏摆运动和转速比下单颗磨粒轨迹图的分布特征,得出以下结论:
(1)不论是定偏心式研磨抛光,还是偏摆式研磨抛光,均需选择合适的偏心距,过大或过小的偏心距都会导致轨迹非均匀性变差,从而影响已加工工件表面质量。
(2)引入偏摆运动有利于改善轨迹非均匀性,提高被加工工件表面质量。通过研究不同的偏摆运动参数,可以发现:当偏摆振幅和偏摆角度分别在15 mm和30 °左右时,轨迹非均匀性系数可减小到0.058;在偏摆角速度与工件旋转角速度的比值k取整数时,轨迹非均匀性系数变差,可达0.284,当k取小数且小数位数越多时,轨迹非均匀越好。
(3)通过比较有无偏摆运动下的单颗磨粒轨迹图,可以发现:偏摆角度在0°~30°之间时,轨迹分布较为均匀;而当偏摆角度过大时,轨迹分布将越来越不均匀,这与理论分析的结果吻合。此外,不论有无偏摆运动,在转速比为小数时,都能获得较为均匀的轨迹分布。

