城市轨道交通联系测量的研究与应用

何 伟

(上海市测绘院,上海200063)

0 引 言

其中,γ为地下起始边方位角误差,ρ=206 265为换算系数,S为隧道长度,Δ为方位角引起的贯通误差。假设γ=±4″,S=1 500 m,则引起的贯通误差为±29 mm。可见起始方位角误差对隧道的贯通影响是极大的。上海轨道交通11号线2期主要采用的方法为导线直传法和联系三角形法。

联系测量是隧道控制测量工作的重要环节,是实现城市地下隧道顺利贯通的关键与核心,同时也是整个隧道测量最难控制的环节[1-3]。联系测量包括高程联系测量和平面联系测量,高程联系测量因高程传递较为简单,本文不再赘述。而平面联系测量方法主要包括导线直传法、投点仪法、陀螺经纬仪联合定向法以及联系三角形法等[4]。

根据上海轨道交通的建设经验,城市轨道交通地下隧道长度一般为800～2 000 m,地下起始边方位角误差引起的贯通误差计算如下:

1 导线直传法

导线直传法即采用精密导线测量的方法传递坐标和方位。此方法工作量小,作业简便。导线直传法的水平角观测具有边长很短、倾角很大、水平角值较小等特点。

水平角观测的误差主要受仪器的三轴误差、仪器对中误差及目标偏心误差影响。

1.1 仪器三轴误差的影响

仪器三轴误差中视准轴误差和横轴不水平误差的影响可采用盘左、盘右观测或多测回测量取平均值的方法予以消除,竖轴倾斜误差对水平观测方向的影响(即竖轴倾斜改正数)Δv可按式(2)计算:

式(2)中,n为水准器气泡偏离中央的格数;τ为水准器格值;α为观测方向的垂直角。

1.2 仪器对中误差的影响

由于导线边很短,若采用安置脚架的方式设站,仪器的对中误差对水平观测方向值有较大影响。因此,在导线布设时各导线点均须埋设具有强制对中装置的观测墩或带有内外架式的金属吊篮,这将有效消除或减弱仪器对中误差的影响。

1.3 目标偏心误差的影响

由地上向地下传递的边长较短(10～20 m),觇牌中心与基座旋转中心不一致产生的误差,会给方位角误差传递带来不容忽视的影响。因此,测量前应对觇牌进行检验和校正,确保符合使用要求。同时应配置附有精密水准气泡(长气泡)的基座架头来整平对中。此外,在方位传递时,照准目标的长、短边距离之比约10∶1,为了减少仪器调焦引起的误差,可采用同一方向正倒镜观测法,其测量步骤为:先盘左、盘右观测零方向,再瞄准另一方向调焦后,对盘右、盘左进行观测。

2 联系三角形法

联系三角形法测量适用于井口小、深度大的竖井测量。该方法的精度较高且稳定,在城市轨道交通地下隧道的联系测量中应用较多,其缺点是工作量较大,作业过程繁琐,设备安装较为复杂(图1、图2)。

图1 联系三角形剖面示意图

图1中,A点为井上控制点,O1、O2为投影钢丝,B为井下控制点。

我们从外部所看到的，会计电算化是将计算机技术应用到会计核算工作中去，通过计算机去完成那些原本属于会计工作人员的工作，减少会计工作人员繁杂工作的工作量，进而提高会计核算的速度和精度。从其内部却可以看到，会计电算化不仅仅是核算工具和核算方法的改进，而是会改进会计工作人员的工作分工，而会计工作人员的素质也会提高，会计工作人员的知识结构也会发生改变，会计工作效率也会大大提高，会计工作的质量也会有飞跃性变化。实行会计电算化，要求会计人员在了解自己的专业知识即会计专业知识的前提下，又要掌握电子计算机的相关知识，因此，使会计人员接触到更多层面的知识，从而提高会计人员的素质。

图2 联系三角形原理示意图

首先,由井上控制点A测定与钢丝间的角度ω、α以及三角形ΔAO1O2的三边距离a、b、c(现通常在钢丝上粘贴反射片直接测定),并计算出钢丝的坐标以及它们之间的方位角。然后,在井下认为钢丝的坐标和方位角己知,同样由控制点B测定与钢丝间的角度ω'、α',以及三角形ΔBO1O2的三边距离a'、b'、c',实现把坐标与方位的传递。

2.1 联系三角形法的注意事项

联系三角形应布设成直伸形状,竖井中悬挂钢丝间的距离a应尽量长;联系三角形锐角α和α'宜小于1°,呈直伸三角形;b/a及b'/a宜小于1.5;联系三角形测量宜选用直径0.3 mm的钢丝,悬挂10 kg重锤,且重锤应浸没在阻尼液中;联系三角形边长测量可采用光电测距或经检定的钢尺,每次独立测量3测回,每测回3次读数,各测回较差应小于1 mm。地上与地下测量同一条边的较差应小于2 mm。钢尺丈量时应施加钢尺鉴定时的拉力,并进行倾斜、温度及尺长改正;角度观测时应使用I级全站仪,测角中误差应在±2.5″之内。

2.2 改进的联系三角形法

为了提高联系测量的精度,王铁生等[5-7]提出了一系列改进的联系三角形方法:如双联系三角形、移动吊锤线法、双站联系三角形法等(图3)。

图3 双联系三角形法示意图

2.2.1 双联系三角形法(三丝法)(图3)

双联系三角形法的方向传递可分为两组:S-＞A-＞O3-＞O2-＞B-＞T方向和S-＞A-＞O3-＞O1-＞B-＞T方向。双联系三角形法相当两次独立传递方位,使用该方法井下起始边精度可提高约倍但该方法对设备要求较高,占用空间较大,且当投向误差较大时,误差积累较大。

2.2.2 移动吊锤线法

2.2.3 双测站联系三角形法

相对以上方法,双侧站联系三角形法则更为方便。在近井点处设置成双测站A和A',然后分别进行两次独立的联系测量。联系三角形须满足延伸形状的条件,所以测站A和A'的间距应较小(图4)。崔旭升等[7]提出可以在强制对中墩上设置两个对中中心作为双测站,该方法操作简单,容易实现。

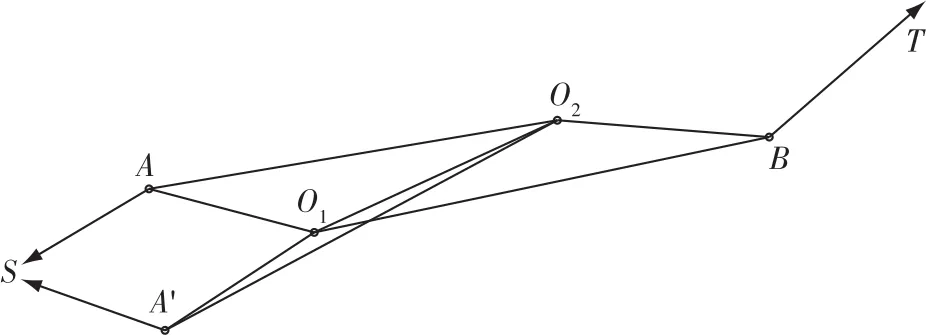
图4 双测站联系三角形法示意图

双测站联系三角形法的方位传递路线分别为S-＞A-＞O2-＞O1-＞B-＞T方向和S-＞A'-＞O2-＞O1-＞B-＞T方向。该方法同样可达到增加检核条件和提高定向精度的目的,且观测时间较短,作业强度较低,实现过程比三丝法更容易。

3 工程实例

上海轨道交通11号线二期工程线路规划起点为长宁区华山路中间风井。全线共设车站13座及停车场1座。二期工程的联系测量主要采用了导线直传法和联系三角形法进行传递。

3.1 两种方法的优缺点比较

(1)联系三角形法点位不固定,每次控制导线复测时都需重新布设点位。直接传递法采用强制归心点,可以避免多次布点所带来的繁重工作量。

(2)联系三角形法需要花费大量人力和物力,但其适用于井口小且深度大的竖井联系测量,且该方法精度稳定。直接传递法适合于井口大、深度浅等目标的测量,如明挖车站或明挖隧道等,该方法具有工作量小、精度高及简单易行的优点。

3.2 两种方法精度比较

联系三角形法误差来源有:① 钢尺因温度、尺长等产生的量距误差;② 钢丝垂线因风力摆动产生的误差等。而导线直传法误差主要来源于仪器的三轴误差、仪器对中误差及目标偏心误差的影响。

上海轨道交通11号线二期工程三林站至济三风井区段始发井的深度约为15 m,井口宽度为20 m,为保证隧道顺利贯通,始发井现场同时采用导线直传法和联系三角形法两种方法测量,并取平均值作为最终成果指导施工(表1)。

表1 井下起始边方位角数据

由表1可看出,导线直传法和联系三角形法的成果差异较小,最大互差仅为3.0″,且同时证明2011年12月上行线的井下起始边发生了变化。所以,这两种方法都是可靠的,并可以互相校核。

4 结 语

导线直传法和联系三角形法是目前我国城市地下隧道平面联系测量所使用的主要方法。本文以上海轨道交通11号线二期工程为例,使用这两种方法测量,得出,导线直传法和联系三角形法的成果差异较小,结果准确可靠。

在使用这两种方法时还需注意以下几个问题:① 应根据施工现场情况,灵活选择导线直传法或者联系三角形法;② 两种方法都应选择较高等级的仪器进行观测,如I级全站仪;③ 施测前应对仪器进行严格的检验、校正;④ 选择联系三角形法时应合理设计三角形的图形,严格满足相关规范要求。