搅拌罐内基于EDEM-FLUENT耦合的多相流混合数值模拟
王建明, 邱钦宇, 何讯超
(山东大学 机械工程学院,山东 济南 250061)
0 引言
在液体环境中添加固体催化剂可以催化液体环境中的化学反应,这是工业上常用的提高生产效率的做法,但是单纯添加固体催化剂可能会产生固体催化剂在液体中的漂浮或沉降,所以需要搅拌使固体催化剂游离在液体环境,这一过程的固体、液体甚至气体的混合状态会因催化剂的性质或搅拌的参数而有所不同,对此,国内外学者展开了诸多研究.在计算固-液两相流混合问题时,多数学者将固体相和液体相均视为连续的流体,通过获取各相的浓度及分布状况来描述混合效果,这种替代方法忽视了离散介质的形状、粒级及其相互作用[1].曾彤等开展水模实验研究,主要分析搅拌器转速及浸没深度与固体颗粒卷吸数量和卷吸高度的关系,并得到最优的搅拌器转速和浸没深度的阈值[2].童长仁等采用滑动网格法和VOF法,对容器形状、有无挡板和挡板宽度等影响自由液面形状的因素进行研究,结果表明:在无挡板圆柱形容器中,自由液面漩涡深度与搅拌器转速呈近似线性关系,有无挡板的方形容器均能抑制水平环流造成的漩涡[3].杨锋苓等以中心和偏心无挡板搅拌槽为研究对象,首次采用分离涡模型和VOF法研究搅拌槽内湍流状态下的自由表面及流场特性,发现仿真结果稍低于文献中的实验结果,证明该方法适用于研究搅拌槽内自由表面的流动问题[4].高玉米针对KR法搅拌罐内的流动问题,运用FLUENT软件进行数值仿真,采用VOF(volume of fluid)法捕捉自由液面漩涡,结果表明:液面漩涡随搅拌时间逐渐形成,由搅拌初期的不规则波动发展到后来具有一定深度、稳定的抛物线状漩涡,液面漩涡的形成对实现固体颗粒与流场的充分混合有积极影响[5].Glover等使用VOF法和剪应力传输模型对搅拌槽内的湍流流动和多相流混合情况进行仿真分析,发现自由表面的速度严重影响槽内固体相的浓度分布[6].李良超等通过使用双电导电极探头测量槽壁附近的液相速度,开展搅拌槽固液两相体系混合的试验研究,结果表明:当槽内固相浓度较低时,固相离底悬浮所需的临界液相速度仅与其尺寸、形状及密度等因素有关,而与桨型、桨的离底间隙等因素无关[7].杨敏官等采用试验方法主要研究搅拌器转速、叶轮离底高度和固相浓度等因素对两相流混合效果的影响,结果表明:槽底中心位置和罐壁区域会产生物料堆积;较低的叶轮离底高度有利于槽内固体颗粒的混合[8].Tamburini等采用非侵入式的LSIA技术测量了固-液两相体系中的固体颗粒浓度,发现固体颗粒主要聚集在叶轮平面上方和下方的两个环形面内,当粒子质量或浓度较大时该现象更为明显[9].张强强采用DEM-CFD耦合技术对多种颗粒模型在水中的沉降过程展开数值研究,通过对颗粒运动过程的跟踪,得到颗粒下落和回弹过程中随时间变化的竖向高度和速度,仿真结果与实验结果有较好的一致性[10].
大多数学者在固-液两相流数值研究中将固体颗粒视为另一连续相,以固相和液相的浓度分布评判固-液混合效果,显然离散的固体颗粒与连续流体相的物理特性差别显著.笔者首次应用EDEM-FLUENT联合仿真技术进行搅拌操作中固-液-气三相流数值建模,其中固体颗粒采用离散元法建模,水和空气采用连续流体相建模,使用VOF模型捕捉气液分界面,据此可获得固体颗粒的运动轨迹和流场特征参数的动态仿真结果,以便于对工艺效果进行直观显示并做相应评价.
1 固-液-气多相流混合模型
1.1 EDEM参数设置
(1)固体颗粒参数设置.EDEM-FLUENT耦合模型属欧拉-拉格朗日模型,其中用欧拉法控制液体和空气的连续介质,而用拉格朗日法控制离散相的固体颗粒,假设采用等直径、同材质的固体颗粒,EDEM软件会根据提供的颗粒直径和密度计算出质量和体积.利用ICEM软件划分好的网格导入EDEM Geometry选项卡中,设置重力加速度.在搅拌操作中,需要考虑不同离散形式的固体之间的相互碰撞以及固体与罐壁碰撞,故在EDEM软件中使用Hertz-Mindlin无滑动接触模型.搅拌罐和固体颗粒参数设置如表1所示.
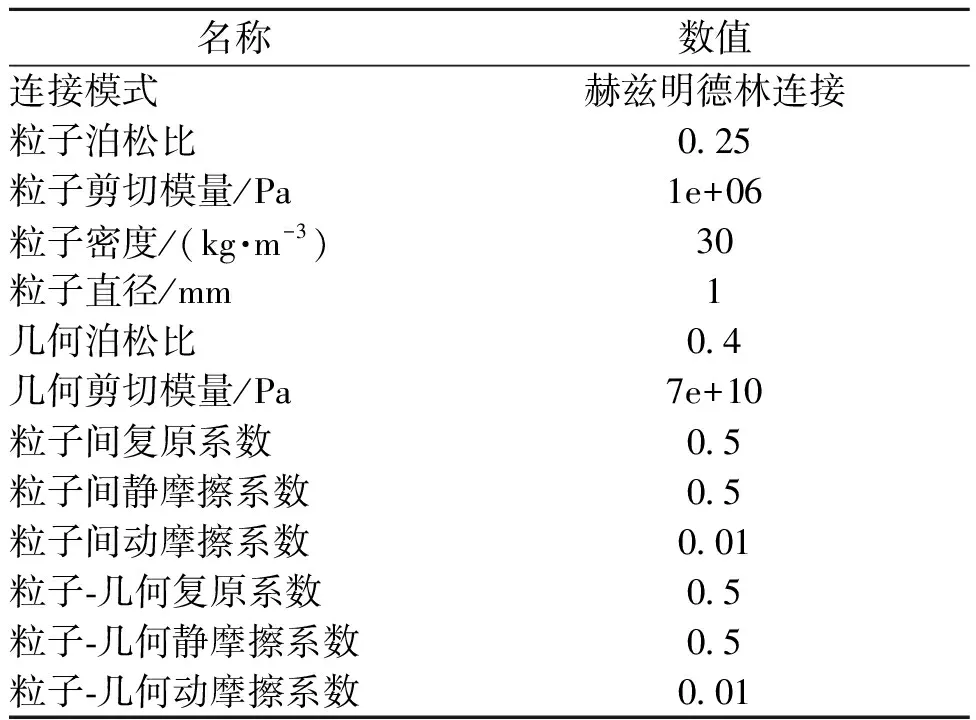
表1 EDEM软件中搅拌罐和固体颗粒的属性设置
(2)颗粒工厂设置.在搅拌操作环节中,固体颗粒从颗粒工厂进入搅拌罐,为了模拟该进入过程,在自由液面上方40 mm处设置4个对称分布的直径为160 mm的球形颗粒工厂,考虑到颗粒数目受计算能力限制,设置每个颗粒工厂在1 s内随机产生500个固体颗粒,颗粒通过自由落体运动下落到液面上.
(3)时间步长设置.固体颗粒在发生接触碰撞过程中,以瑞利波形式消耗的能量占总能耗的70%,在EDEM中将时间步长设为2~5 s.
(4)建立耦合连接.将EDEM中关于耦合接口的工具窗口打开,选择Start,使EDEM处于监听耦合信号状态,等待与FLUENT建立连接.
1.2 FLUENT参数设置
(1)加载edem_udf耦合文件.调用FLUENT中Define菜单下的Compiled命令加载edem_udf文件夹.
(2)模型及数值算法设定.采用非结构四面体单元进行网格划分,将网格模型导入到FLUENT中,并做网格质量检测.由于要捕捉气-液相的分界面探究自由液面的变化对固体分散的影响,使用VOF模型,设置空气为第一相,液体为第二相,在气-液分界层处设置标准大气压,搅拌罐顶部设置为压力出口,将罐体侧壁及底面定义为无滑移壁面边界条件;将位于静区域中的搅拌轴定义为运动壁面边界条件,其绝对转速与动区域一致;将动区域搅拌器壁面定义为运动壁面边界条件,其相对转速设为零,即搅拌器与动区域网格同步旋转.
(3)耦合模型设置.在FLUENT的Model选项卡中选择edem couple模型,选用拉格朗日耦合模型,将固体模型视为离散的固体相.耦合区域为整个流体域,包括动区和静区两部分,采用默认的松弛因子.由于需要考虑液体与固体颗粒之间的曳力和液体对固体颗粒的浮力,故选择Ergunand Wen & Yu曳力模型和固-液两相升力模型.
1.3 仿真模型验证
为验证上述仿真模型的正确性,开展了相应的水模试验研究,该水模试验装置如图1所示,搅拌罐直径为523 mm,液体深度为414 mm,搅拌器直径为203 mm,潜入深度为276 mm,叶片数目为4片,转速为160、240、320 r/min,通过在搅拌罐侧壁竖立标尺,分别测量自由液面稳定状态下的漩涡深度和漩涡高度,并与相应参数数值模拟结果进行比较.

图1 水模试验装置Fig.1 Water model experiment device
图2为水模试验和数值模拟得到的漩涡深度及高度随转速变化图.从图2可以看出,数值模拟和水模试验得到的自由液面漩涡深度和漩涡高度基本一致,其中两者的最大相对误差仅为3.1%、6.5%.该对比结果验证了上述数值模型的正确性和有效性.

图2 数值模拟与水模试验结果对比Fig.2 Comparison between water model experience and numerical simulation
对图2中数值模拟曲线进行多项式拟合,分别得到漩涡深度和漩涡高度随转速变化的多项式表达,
H1=1.906n-195.8,
(1)
H2=0.269n-4.167.
(2)
2 耦合模型仿真结果及分析
2.1 自由液面变化和流速场分布
基于EDEM与FLUENT联合仿真的方法,在FLUENT中使用VOF法捕捉气液分界层,在EDEM中使用离散元模型追踪固体颗粒群的运动过程.为了探究该耦合模型中自由液面漩涡深浅和流速场对离散化固体颗粒运动规律的影响,首先讨论自由液面的变化过程.
图3是在4叶搅拌器转速为160 r/min,浸没深度为214 mm工况下,通过FLUENT软件获取的不同时刻下自由液面变化过程,蓝色部分为空气,红色部分为冷态水.由图3可以看出,整个搅拌过程中存在明显且均匀的带状气液分界层,初始时刻自由液面保持静止,随着搅拌操作的持续进行,自由液面逐渐下凹,呈V字形状,自由液面的漩涡底部延伸至搅拌器叶轮上表面后达到稳定状态.
图4为上述工况下的搅拌罐内流速场矢量图.由图4可以看出,罐内叶轮四周流速分布相对均匀,在叶端处存在径向射流,在运动至搅拌罐壁时形成上下两部分回流,向上流动的液体受卷吸向液面处流动,向下流动的液体大部分返回至叶轮处继续循环,小部分液体在壁面涡流的带动下构成一个循环.搅拌器叶轮正下方存在流动死区,严重阻碍了固体颗粒与此处液体的混合.
2.2 固体颗粒分布变化
通过基于离散元EDEM软件和FLUENT软件的联合仿真,可获取单个颗粒或颗粒群在不同时刻的位置、速度和受力等信息.
图5为上述工况下,通过EDEM软件获取的不同时刻下固体颗粒在搅拌罐内的分布状况图.由图5可以看出,在初始时刻,离散的固体颗粒从液体表面随着搅拌过程的逐渐进行,自由液面逐渐下凹,固体颗粒在浮力和液面波形作用下聚集在漩涡中心处,并开始沿搅拌轴向下运动;当自由液面漩涡底部延伸至搅拌器叶轮上方时,随水流运动下沉的固体颗粒被叶轮打散,然后沿叶轮径向向外运动;当颗粒运动受到搅拌罐壁的阻碍时,沿罐壁分成上下两股流动;向上流的固体运动至液面处,再次被卷入漩涡中,开始新一轮循环流动;向下流的固体颗粒在随流体运动过程中,一小部分颗粒受到浮力与搅拌罐壁碰撞的影响做无序运动,大部分颗粒则被重新卷吸到搅拌器叶轮处,进而被叶轮打散,开始下一轮循环流动.由此可以看到,在多相流混合搅拌罐内,固体颗粒在搅拌器作用下形成4股主要的循环流动.
2.3 固体颗粒分布统计
为了直观分析固体颗粒在搅拌罐内的分散特点,利用EDEM软件建立Grid Bin Group,将稳定流场划分成等体积的3×1×4网格区域,如图6所示.考虑到流场的对称分布,选取A、B、C、D、E、F 6个网格区域统计0~10 s各区域内的颗粒数目,统计结果如图6、图7所示.
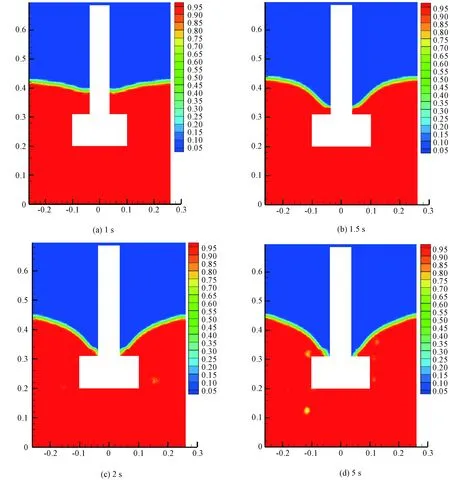
图3 不同时刻的自由液面变化图Fig.3 Free surface changes at different time

图4 XOZ断面流速场矢量图Fig.4 Velocity field vector at XOZ section
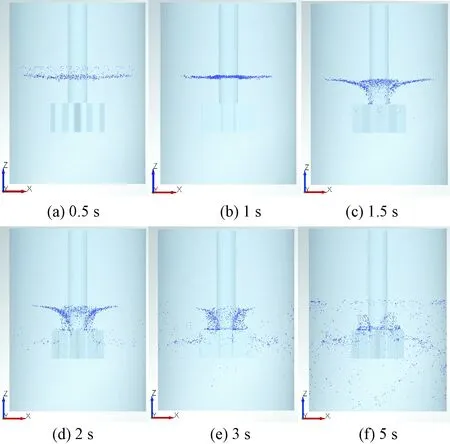
图5 不同时刻固体颗粒位置分布图Fig.5 Solid particle position distribution at different time

图6 搅拌流场区域划分Fig.6 Regional division for stirring flow field
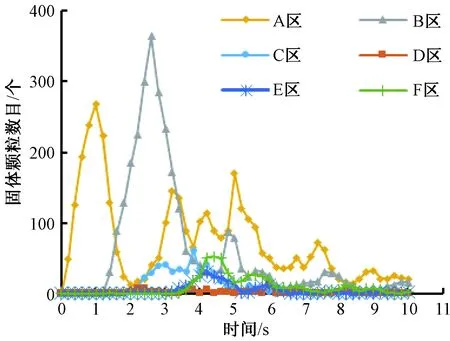
图7 不同区域固体数目随时间的变化Fig.7 The number of solid agents in different areas changes with time
网格A区域是液面靠近搅拌罐壁的区域,在初始时刻,固体颗粒以每秒500粒的产生速度从颗粒工厂自由下落,在1 s时达到最大值.当颗粒向搅拌轴附近聚集,并随自由液面漩涡下潜时,网格A区域中的颗粒数目逐渐减少.当固体再次向液面聚集时,A区域中的固体颗粒数目逐渐增多.
网格B区域靠近搅拌器叶轮端部,当自由液面漩涡底部延伸至叶轮上部,固体被打散并沿径向排出,进入B区.当B区的颗粒运动至搅拌罐壁时,将分流成向上进入A区和向下进入C区的两部分.
网格C区域靠近搅拌器叶轮左下方,由于固体颗粒密度较小,沿径向排出的固体颗粒受到搅拌罐壁阻碍时,大部分颗粒上浮至A区域,约1/3的颗粒进入C区域,使得固体颗粒在搅拌器叶轮上方的数目比下方多.
网格D区域为搅拌罐底部,网格E、F区域位于搅拌器叶轮的正下方,受流动死区的影响,这3个区域内的固体颗粒数目相对较少.
图8为多相流混合模型中,采用欧拉-欧拉法将固体颗粒视为拟流体,通过初始时刻平铺式投放固体颗粒得到稳定状态下固体浓度分布图,与笔者基于EDEM-FLUENT耦合模型下得到的不同区域固体颗粒数目统计结果比较可知,稳定时刻下二者的固体颗粒分散规律基本一致,即固体颗粒主要分布在搅拌器叶轮周围的扇形区,且搅拌罐上部分布的固体浓度较下部大,而受到流动死区的影响,叶轮正下方固体颗粒浓度极低.
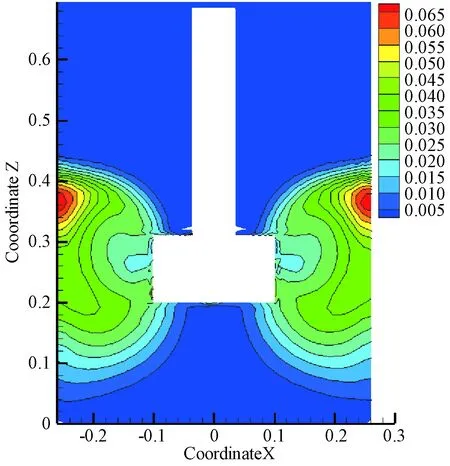
图8 平铺式工况下固体浓度分布云图Fig.8 Solid state distribution cloud map under tile condition
2.4 单个固体颗粒运动轨迹
利用EDEM软件可以提取单个颗粒随时间变化的运动轨迹,观察不同固体颗粒的不同运动轨迹;图9(a)展示了固体颗粒从颗粒工厂下落后受搅拌作用,随自由液面漩涡下移,在碰撞搅拌器叶轮后,被打散沿径向排出,在受到搅拌罐壁阻碍后,向上运动至液面,并在此后继续被液体卷吸,进入循环流动.图9(b)展示了被搅拌器叶轮径向排出的固体颗粒在接触到搅拌罐壁后,开始沿罐壁向下运动的轨迹,并在流场带动下返回至叶轮,进行下一轮循环流动.
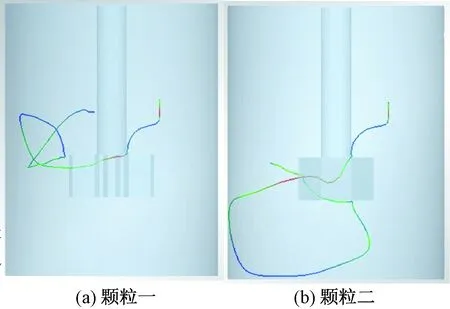
图9 单个颗粒运动轨迹Fig.9 Motion trajectory of single particle
3 结论
研究结果表明:EDEM-FLUENT耦合技术可以运用到搅拌罐内多相流混合数值模拟中,其模型更接近实际工况,通过对自由液面、流场和固体颗粒分散的分析可知,固体颗粒分散形式受自由液面漩涡位置和流场的影响,当自由液面漩涡底部延伸至搅拌器叶轮处,固体颗粒被打散,且受到流场径向流特点的影响沿径向排出.该多相流混合过程较为复杂,只有将固体颗粒处理成离散相才更符合实际,才能得到包括单个固体颗粒运动轨迹在内的更加直观和丰富的仿真结果.通过对流场内固体颗粒数目的统计可知,基于EDEM-FLUENT耦合的固-液混合数值模型,得到的固体颗粒分散情况与利用欧拉法得到的结果相一致,对于轻密度的固体颗粒,其在搅拌器叶轮上部分布范围较广,在搅拌罐底部和叶轮正下方的流动死区固体的数目较少或浓度极低.

