基于位置转移时空规律的用户签到位置预测*

刘攀登，李 川，李晓娟

四川大学 计算机学院，成都 610065

1 引言

随着Foursquare、Gowalla、Micro-blogging、大众点评网等基于位置的社交网络（location-based social network，LBSN）的广泛应用，基于LBSN的位置预测成为近年来的研究热点之一。准确的位置预测在城市规划[1-2]、交通预测[3-4]、广告推送[5-6]以及疾病预防[7]等方面具有非常重要的应用价值。

现存用户移动性规律发现方法，如马尔科夫模型、PMM（periodic mobility model）、W3（who，when，where）等虽各有所长，但仍存在如下缺陷：（1）不能将时间对于用户访问位置变化的影响真实、量化地反映出来；（2）不能将地理位置间前后相继、相互关联的影响真实、量化地反映出来。

现实生活中，人类的移动行为在时间上是连续的，前一时刻的移动行为必然影响下一时刻的行为，前一状态的位置必然影响下一状态的位置。马尔科夫过程与这种直观的移动行为相吻合，被广泛应用于位置预测模型中[8-11]。然而，该方法有如下缺陷：（1）难于实现复杂度和预测精度间的平衡：虽然马尔科夫模型阶数的增加会提高算法的准确率，但算法复杂度也会随之增加。（2）忽略时间的影响：用户移动行为和时间有着紧密的联系，但使用马尔科夫模型来预测用户的位置会忽略时间的影响。如，工作日上午9:00，人们一般在公司上班，但周末的上午9:00，他们可能在家休息或者在旅行。（3）忽略移动轨迹的前后地理位置间的关联：轨迹绝不是孤立的，它们彼此联系。如，从家出发去商场，接着到办公室（家庭—商场—办公室）这条轨迹与（家庭—商场—餐厅）轨迹是有关联的。但使用马尔科夫模型建立转移概率时，研究者则假设轨迹独立。

2011年，Cho等人[12]提出PMM模型，针对单个用户，将用户签到数据按时间分段，分别利用高斯混合模型对用户不同时段的签到数据进行建模从而实现位置推荐。但该模型只能对单一用户逐个建模，缺乏通用性。其次，该模型必须基于特定用户历史数据进行建模，难以实现对新用户的位置推荐。更值得注意的是，该模型未系统地考虑时间因素对用户移动行为的影响，对每天相同时段进行相同位置推荐。

2013年，Yuan等人[13]提出概率模型——W4（who，where，when，what），该模型基于tweet数据内容（包括用户ID、文本内容、时间、位置等），建立贝叶斯网络，采用EM算法来估计模型的参数。然而此模型参数的调整较为复杂，且需要完备的结构化信息，这些信息在多数情况下不能完整获取。更重要的是，该模型未考虑地理位置之间前后相继的转移影响。由于本文所采用的数据集中不包括tweet的文本内容，故本文与W4的变形——W3模型进行对比。

综上，现存方法均未能系统考虑用户的位置转移因素、位置转移所体现的真实的时间规律，亦未考虑用户群体的影响。

为解决上述问题，本文提出挖掘用户签到位置转移变化的规律性。为描述用户位置的转移变换，本文提出簇标记转移矩阵，以描述在特定时刻用户从某簇转移到不同簇的签到记录频次分布情况。借助簇标记转移矩阵，本文提出基于向量自回归的位置转移演化算法（location transfer evolution algorithm based on vector autoregressive，LTE），挖掘簇标记转移向量随时间变化的规律。可根据规律预知未来某时刻或多个时刻的簇标记转移向量，进而可以为用户进行位置推荐或预测。然而，由于用户的签到行为是随机的，用户签到数据在所选时间粒度上是不连续的，簇标记转移矩阵序列的生成同样是一项具有挑战性的工作。基于Foursquare、Gowalla纽约、东京真实用户签到数据集，本文结合对比算法进行了大量、有效性对比分析。实验表明，本文所提出的基于向量自回归的位置转移演化算法，具有更高的预测有效性和预测精度，能有效完成用户位置的准确预测。

2 簇标记转移矩阵

由于用户签到点具有随机性和多样性，为克服签到点细微差异所造成的高维数据分析处理中的组合爆炸问题，本文对所有时刻的用户签到点按经纬度进行聚类。本文采用基于K-means的位置聚类算法[14]，遵循欧式距离最小化原则，把样本点集划分为若干个簇，使得簇内样本点相似度尽可能高，且簇间样本点相似度尽可能低。K-means聚类算法将用户的签到样本集D划分为k个不相交的簇{Cl|l=1,2,…,k}，其中相应地，用λ∈{1,2,…,k}表示样本的簇标记。该算法将距离相近的签到点划分到同一个簇，最终将得到若干个独立且紧凑的簇。

定义1（簇标记转移矩阵C）设N为簇标记的总数，存在矩阵C(N×N)，对于任意1≤i,j≤N，矩阵元素Cij表示从簇标记λi到λj的签到记录频次，则矩阵C(N×N)称为签到数据集D上的簇标记转移矩阵。所有时刻簇标记转移矩阵按时间的先后顺序排列将形成簇标记转移矩阵序列S={CT1,CT2,…,CTT}。

基于定义1，可由T和T+δ（δ为簇标记转移矩阵序列的时间粒度）时刻的用户签到记录的簇分布，生成T时刻簇标记转移矩阵。如图1所示。设用户的签到点簇标记总数N=4（即簇0、1、2、3），则簇标记转移矩阵C为4×4矩阵。图1（a）～（c）中不同颜色的圆圈表示不同用户的签到记录。图1（a）、（b）中相同颜色的圆圈表示某用户的位置转移情况。如，蓝色圆圈从图1（a）的簇0转移到图1（b）的簇1，则，对应到图1（d）中C01应为1。再如，图1（a）中簇0紫色圆圈和粉色圆圈在T1时刻都转移到图1（b）中的簇2，那么对应到图1（d）中的C02应为2。

Fig.1 Generation of cluster marker transfer matrix sequence图1 簇标记转移矩阵序列

3 基于簇标记转移序列的向量自回归

用户的簇转移是相互影响的。如，用户在某时刻到达簇A，那么该用户在该时刻将不可能同时到达其他簇。向量自回归模型（vector autoregression，VAR）描述多变量时间序列间的变动关系，能够揭示序列的变化规律受其他序列的影响。基于定义1，可获取每个时刻簇标记转移矩阵，将它们按照时间先后顺序排列，即可得到簇标记转移矩阵序列。为方便探索簇标记转移矩阵随时间的变化规律，首先定义簇标记转移向量序列。

定义2（簇标记转移向量序列V）将簇标记转移矩阵序列中的每一个矩阵CTi横向展成向量Vi后所形成的向量序列V={V1,V2,…,VT}称为簇标记转移向量序列，Vi称为i时簇标记转移向量。

多变量时间序列的VAR模型，从变量序列的数据出发，探讨相互之间的动态变化规律，即滞后结构关系，设yt=(y1t,y2t,…,ykt)为k维内生变量向量，εt=(ε1t,ε2t,…,εkt)为k维随机扰动向量，则滞后阶数为p的VAR模型（记为VAR（p））表达式为：

式中，yt是t时簇标记转移向量；Φi(i=1,2,…,p)是第i个待估系数k×k维矩阵；εt～N(0,Ω)，εt每一维独立同分布，但不要求不同维之间相互独立，εt服从以E(εt)=0 为期望向量；cov(εt)=E(εtεt′)=Ω为方差的k维正态分布。

滞后阶数的选择对构建VAR模型至关重要，本文用赤池信息准则（Akaike information criterion，AIC）确定p值，确定p值的方法是在增加p值的过程中，使AIC值同时最小。AIC定义为：

其中，n=k(kp+1)是待估参数的个数，k是内生变量个数，T是样本长度，p是滞后阶数，l由下式确定：

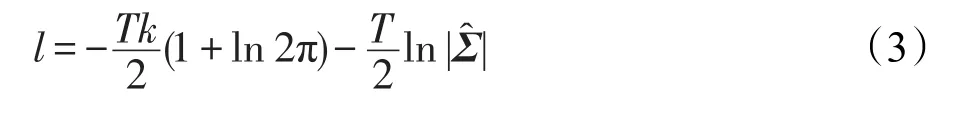
同理，可进行多步预测，预测出未来多个时刻的簇标记转移向量。

4 基于向量自回归位置转移时空规律学习

首先，采用K-means聚类算法对用户的签到数据按照经纬度进行聚类，并对每条签到记录赋以簇标记λ；然后，根据所选的时间粒度δ对签到时间进行标记，为每条签到记录赋以对应的时间标记T。由此，每条签到记录都有对应的簇标记和时间标记。继而得到随时间变化的簇标记转移向量序列，然后利用向量自回归进行建模，从而预测下一时刻或未来多个时刻的簇标记转移向量，如算法1所示。

特定时刻的簇标记转移矩阵，描述的是该时刻由某簇转移到其他簇的签到记录频次分布情况。对每个用户，将用户的签到记录按时间升序排序，若该用户某条签到记录和下一条签到记录在时间标记上是连续的，则更新对应的簇标记转移向量元素值。否则，认为用户在下一时刻仍停留在原地。更详细地说，对某用户连续的两条签到记录，若该用户在t0时刻去往簇标记为λ0的位置，在t1时刻去往簇标记为λ1的位置，若t0和t1的时间标记（分别为T0、T1）是连续的，那么更新T0时簇标记转移向量中表示从λ0转移到λ1的元素值。否则，更新T0时簇标记转移向量中表示从λ0转移到λ0的元素值。由此，可以生成簇标记转移向量序列，最后，建立向量自回归模型以挖掘用户的位置转移演化规律。

算法1基于向量自回归的位置转移演化算法（LTE）

输入：用户签到数据集D={(u0,w0,j0,t0,λ0,T0),(u1,w1,j1,t1,λ1,T1),…,(um,wm,jm,tm,λm,Tm)}，其中u={u0,u1,…,ud}为用户集，w、j、t分别表示用户签到点的纬度、经度和签到时间；聚类个数k；预测步数s。

5 实验分析

5.1 数据集

本文使用Foursquare（基于用户地理位置签到服务）中纽约和东京两个城市的签到数据，以及Gowalla数据集中纽约的签到数据。每条签到记录都有对应的时间戳。时间跨度从2012年4月4日到2013年2月16日。数据集的统计信息如表1所示。本文将每个数据集的最后10个时刻的用户签到记录作为测试集，之前的签到记录作为训练集。

Table 1 Statistics of datasets表1 数据集的统计信息

5.2 评价指标

本文预测未来10个时刻的簇标记转移向量，为使向量分量误差之间具有可比性，即向量分量的误差在同一个数量级上。本文采用离差标准化对误差进行归一化处理，则未来10个时刻的向量分量vj误差转换函数如下：

为评估算法的预测性能，本文采用平均绝对误差（mean absolute error，MAE）和均方根误差（root mean square error，RMSE）作为评价指标，表示预测t时簇标记转移向量的误差，公式如下：

其中，k为簇标记转移向量的维数。

5.3 参数配置

针对每个数据集，本文设置聚类个数为4。因为用户签到数据在时间上是不连续的，所以选取的时间粒度不同，得到的簇标记转移向量序列不同，算法的预测性能也会不同。本文设置时间粒度分别为1,2,…,8（单位：h），学习不同的时间粒度δ对算法预测性能的影响。本文用预测的未来10个时刻的平均误差来度量算法的预测性能。

从图2可知，虽然时间粒度对算法预测误差的影响没有固定的规律可寻，但是选取合适的时间粒度对算法的预测性能有着举足轻重的地位。本文针对3个数据集，选取较为合适的时间粒度。针对Foursquare纽约城市签到数据集，设置时间粒度为5 h，Foursquare东京城市签到数据集，设置时间粒度为1 h，Gowalla纽约城市签到数据集，设置时间粒度为1 h。

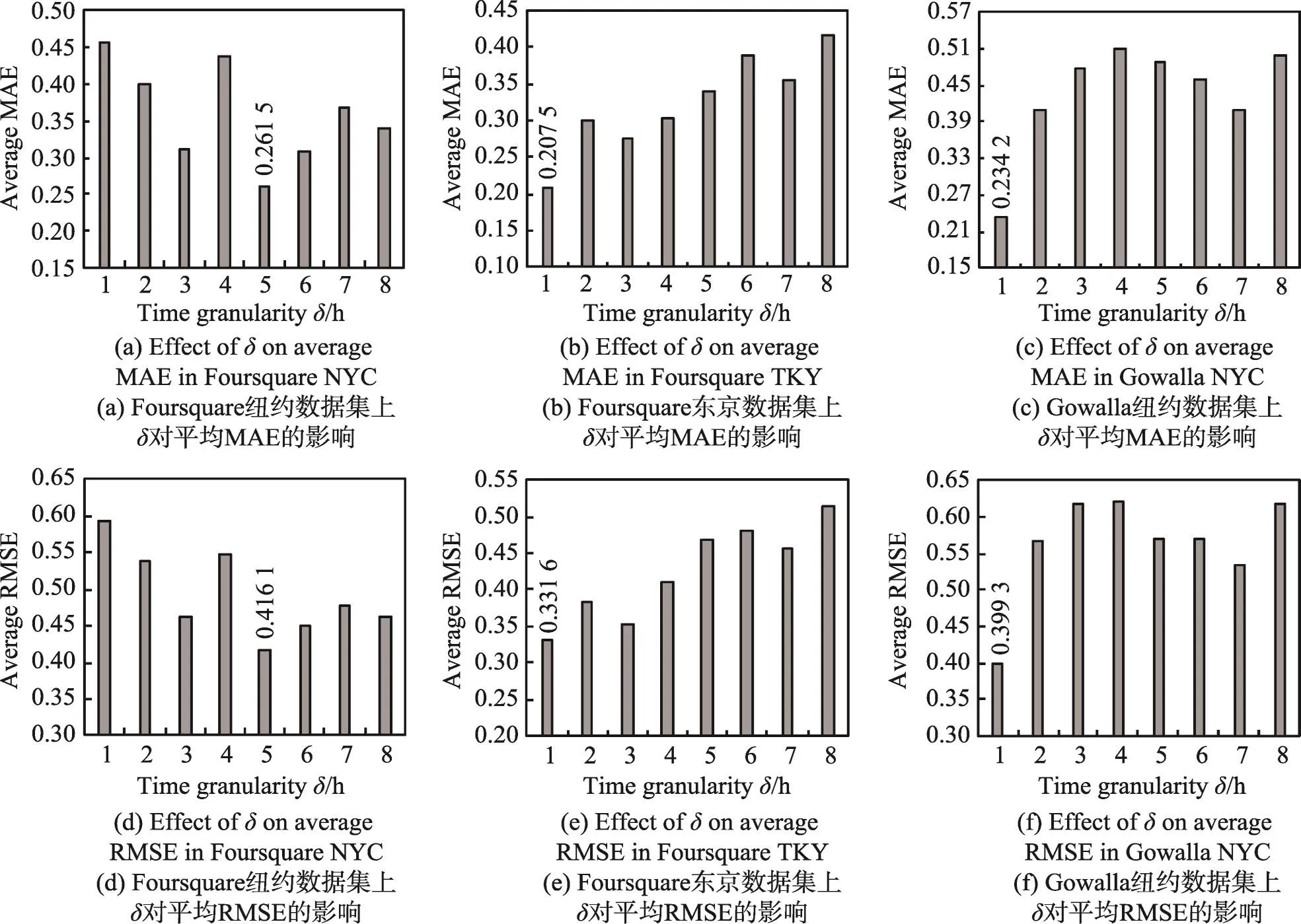
Fig.2 Time granularity adjustment图2 时间粒度参数调整

滞后期对于构建VAR模型至关重要。AIC值越小，表明模型越能有效反映变量之间的关系。阶数参数调整结果见图3。其中横坐标表示滞后阶数，纵坐标是赤池信息量准则，选取使AIC值最小的阶数。针对3个数据集，本文将阶数分别设定为5、11和6。

5.4 VAR有效性验证

为验证本文所使用的技术方案的有效性，对不同学习方法进行较深入的探索与辨析，将VAR模型的预测性能与AR、SMA和SES分别进行对比。

自回归模型（autoregressive model，AR），如果时间序列{yt}可以表示为它的前期值和随机扰动项εt的线性函数：

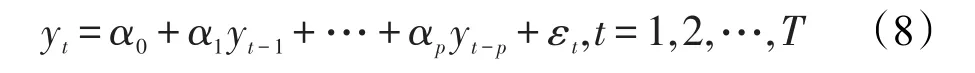
则称该序列{yt}是自回归序列，上式为p阶自回归模型，简记为AR（p）。式中的自变量是时间序列在不同滞后时期的取值，即时间序列{yt}的变化受其自身变化的影响。

一次移动平均法（single moving average，SMA），通过对时间序列逐期递移求得平均数作为预测值的方法叫一次移动平均法，它是对时间序列进行修匀，边移动边平均以排除偶然因素对原序列的影响，进而测定长期趋势的方法。已知时间序列为{yt}(t=1,2,…,T)，T为时间序列总期数，则一次移动平均法的公式为：

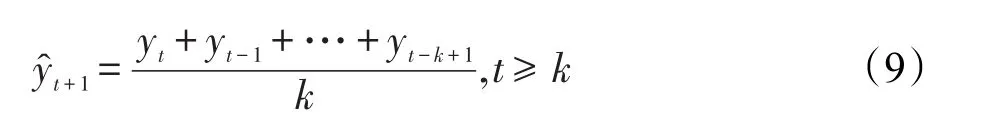
使用时间序列中最近一组历史数据的平均值作为下一期的预测值，移动平均法的“平均”是指对历史数据的“算术平均”，而“移动”是指参与平均的历史数据随预测期的推进而不断更新。

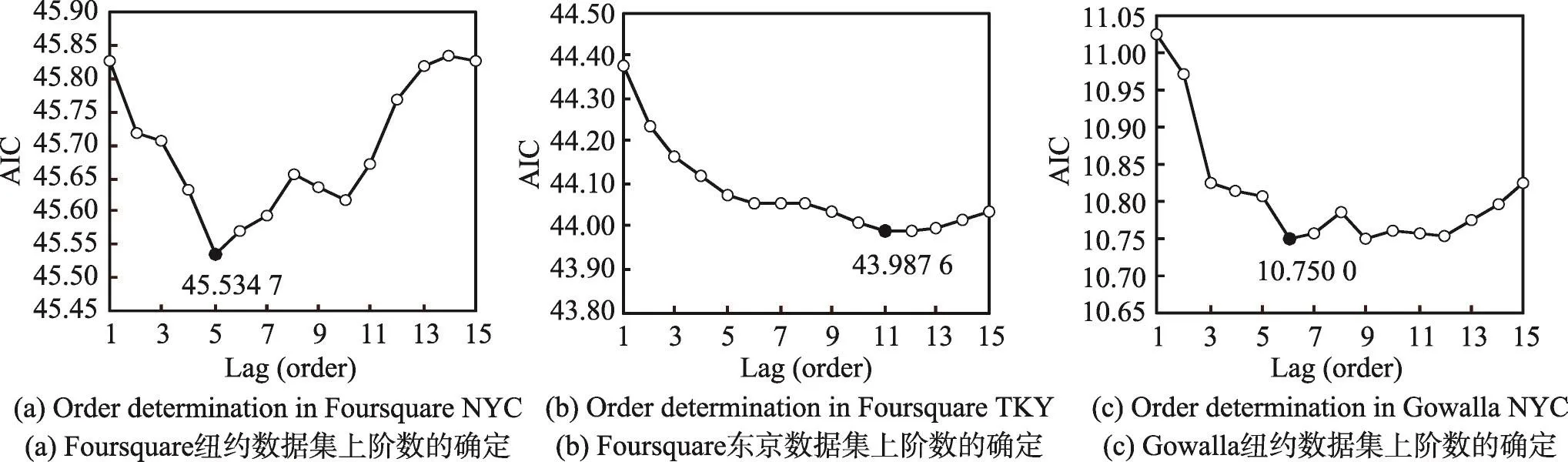
Fig.3 Order determination图3 定阶

简单指数平滑法（simple exponential smoothing，SES），是把本期实际观察值和本期预测值的加权平均值直接作为下期预测值的预测方法。已知时间序列为{yt}(t=1,2,…,T)，T为时间序列总期数，则简单指数平滑法的递推公式为：

其中，α为平滑系数。由于，故依次递推可得：

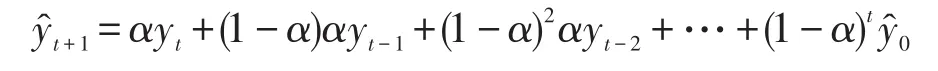
指数平滑法是一种特殊的加权移动平均法，其加权的特点是对离预测期近的历史数据给予较大的权数，对离预测期远的历史数据给予较小的权数，权数由近到远按指数规律递减。

本文通过实验充分验证VAR模型为最佳技术方案，VAR实现较好的性能。具体实验结果如图4至图6，针对Foursquare纽约城市数据集，在其中9个时刻，VAR模型的预测误差低于其他方法。在Foursquare东京城市数据集，有8个时刻，VAR模型预测的准确度高于其他方法，Gowalla纽约城市数据集，在其中7个时刻，向量自回归（VAR）模型的预测性能优于其他方法。这是因为VAR模型是基于簇标记转移向量序列建模，而AR、SMA和SES是基于簇标记转移向量的每个分量序列分别建模的，VAR模型相对于其他方法，考虑多个时间序列之间的相关性，将时间序列分析和多元回归分析有机地结合在一起，有效地提高预测的精度。

5.5 对比实验

本节将所提的基于向量自回归的位置转移演化算法LTE应用于位置预测，并将LTE算法的预测性能与W3和PMM算法进行对比。本节仍然使用以上3个真实的数据集，针对每个数据集，将每个用户的按时间顺序的签到数据以8∶2的比例分为两部分，分别作为训练集和测试集。为评价不同模型的预测性能，本节采用预测的准确度（ACC）作为评价指标，即预测位置中包含多少比例的真实位置。

Fig.4 Prediction performance of different methods in Foursquare NYC图4 Foursquare纽约数据集上不同方法的预测性能比较

Fig.5 Prediction performance of different methods in Foursquare TKY图5 Foursquare东京数据集上不同方法的预测性能比较

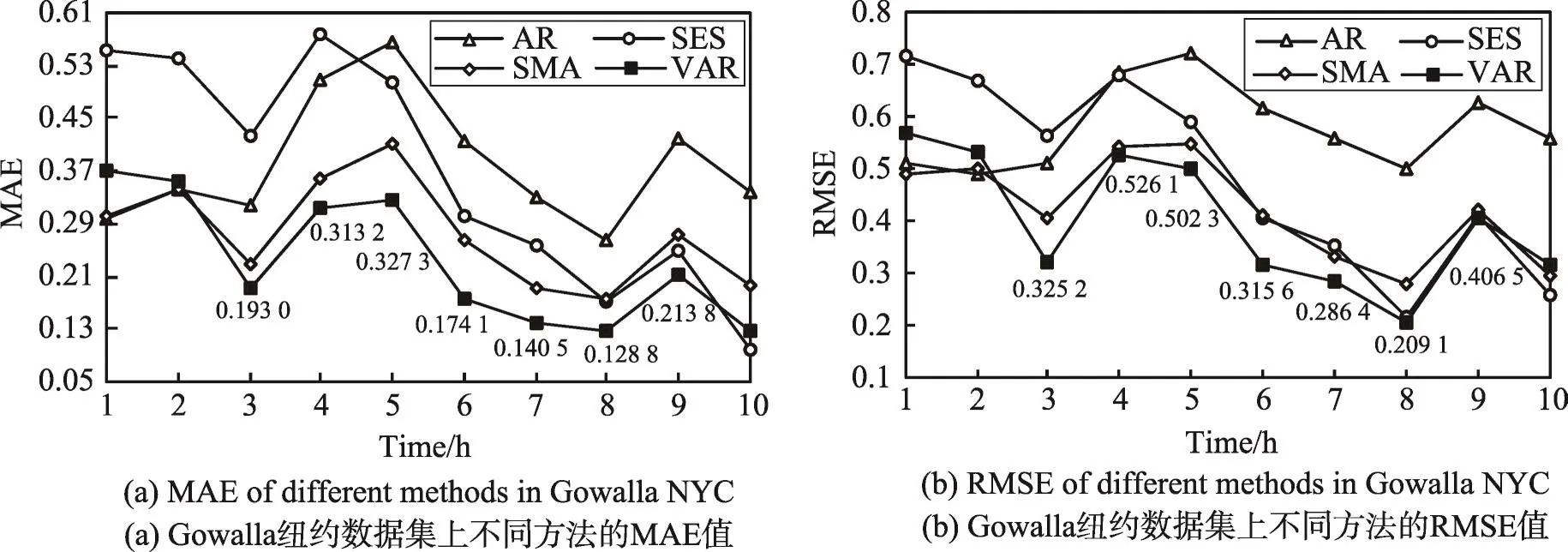
Fig.6 Prediction performance of different methods in Gowalla NYC图6 Gowalla纽约数据集上不同方法的预测性能比较

PMM[12]大多数人的运动具有周期性，其运动方式大多是围绕几个潜在位置按时间进行有规律的往返。该模型假设用户的潜在位置有两个，分别为家庭和办公地，用户的签到数据是由随时间变化的两状态的高斯混合模型生成的。针对单个用户，将用户的签到数据按时间分段，并分别利用高斯混合模型对用户的不同时间段的签到数据进行建模，并使用EM算法进行参数估计，最终训练出该用户在不同时间段的高斯混合模型，从而相应地在不同的时间段为该用户进行位置预测。

W3[13]是W4的变形，相对于W4而言，W3没有考虑文本因素。由于本文所使用的数据集中不包含tweets的文本内容，故本文使用W3模型作为对比实验。W4是一个概率移动性模型，利用tweets文本数据，包括文本内容、地理信息、发布时间和用户ID，从空间、时间和活动三方面发现用户移动行为规律。对于所有的候选位置，按照以下公式计算用户出现在候选位置的概率，并选取概率值最大的Top-k个位置作为预测位置。

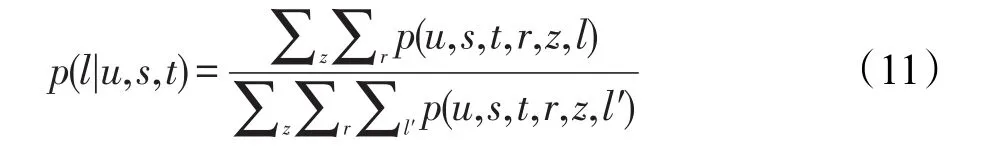
其中，s∈{0,1}，分别表示工作日和周末；u、t、r、z、l分别表示用户、时间、区域、主题和地点。

预测结果如图7所示。在3个真实数据集上的实验表明，本文提出的算法准确率分别达到73.86%、79.25%和76.58%。相对于W3，LTE的准确率分别提升8.76%、21.31%和4.43%。与PMM相比，LTE的准确率分别提升28.97%、38.50%和25.07%。LTE的预测性能有明显优势。这是因为本文算法将时间对于用户访问位置变化的影响真实、量化地反映出来，真正将时间因素真实地建模至移动性规律中，此外，本文算法还考虑位置转移、位置转移时序特征以及大多数用户群体的意见，这些因素的考虑都有利于提高位置预测的准确性。

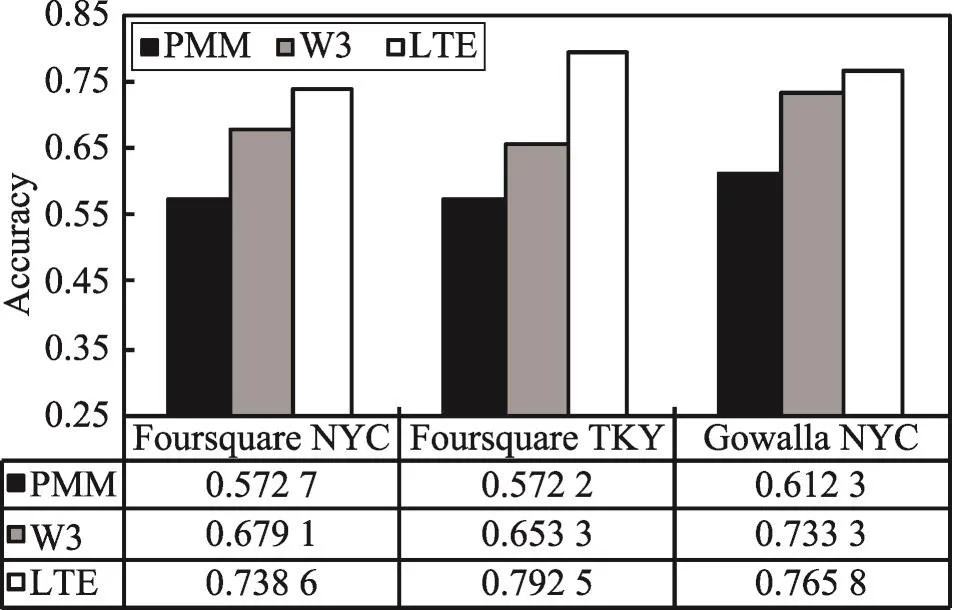
Fig.7 Location prediction accuracy of PMM,W3 and LTE图7 位置预测算法PMM、W3和LTE的准确度对比

6 相关工作

基于位置的社会网络推荐系统使用的主要方法分为以下3类：

（1）基于内容的推荐系统

基于内容的推荐系统的依据是：用户的兴趣应该与系统所推荐位置的描述相匹配。用户的兴趣与位置的描述越相似，用户对推荐的位置可能越感兴趣。在基于内容的推荐方法中，计算出与用户最相似的几个位置，然后按照相似度的大小推荐这些位置。Park等人[15]、Ramaswamy等人[16]将从用户基本资料中发现的用户偏好与位置特征（如标签和类别）进行匹配来做出推荐。这些系统需要用户基本资料和位置功能信息来提高推荐的质量。

基于内容的方法的主要优点是，这样的系统克服了新用户和新地点的冷启动问题。只要新添加的用户或位置有适当的描述性内容，这种推荐系统都能有效地处理。然而，基于内容的推荐系统也有很多弊端：①基于内容的推荐系统没有考虑用户群体的意见，这可能会导致低质量的推荐；②基于内容的推荐系统需要用户和位置的结构化信息，这些信息的获取代价是很大的。

（2）链接分析算法

链接分析算法（如PageRank和HITS）广泛应用于网页排名。这些算法分析复杂的网络结构并提取具有高影响力的节点。Zheng等人[17]扩展HITS算法来发现LBSN中有经验的用户和有趣的位置。每个位置有受欢迎程度的评分，每个用户有旅行经验评分，最终得到用户经验度和位置流行度的排名。Raymond等人[18]扩展基于随机游走的链接分析算法进行位置推荐。

基于链接分析方法的优点是：①考虑用户的经验，并对经验丰富的用户进行评分；②解决冷启动问题。然而，这类方法有一个主要的缺点：它们只能为所有用户提供通用的推荐，忽略了用户的个性化偏好。

（3）协同过滤推荐

在传统的推荐系统中，协同过滤（CF）被广泛使用。CF模型基于以下假设：用户更可能访问相似用户访问过的位置。Cheng等人[19]融合地域影响力和社交信息建立矩阵分解模型，从而进行个性化位置推荐。Jia等人[20]提出SeqRWR方法动态选择在每个时间片对目标用户最有影响力的N个朋友，然后利用所提的TSB模型对朋友影响力的特征建模，预测用户在每个时间片的位置并进行推荐。Liu等人[21]提出IRenMF方法探究周边地理位置的特征，学习用户和位置的潜因子，以提高位置推荐的准确度。Lian等人[22]提出GeoMF模型，首先利用所提的加权矩阵分解解决隐式反馈协同过滤POI推荐的稀疏性，再将空间聚类现象融入到矩阵分解模型中以提高推荐性能。Bao等人[23]提出基于位置和偏好感知的推荐系统，既考虑用户个体偏好又考虑本地专家的意见，从而为用户进行位置推荐。

协同过滤模型的优点是：①不需要位置或用户的结构化描述；②吸取用户群体的意见提高推荐的质量。

然而，CF模型也有缺点：①当数据稀疏，例如用户评分的数量很少，用户-位置的评分矩阵是非常稀疏的，从而导致协同过滤模型做出的推荐是不准确的；②由于系统中有大量的用户和位置，相似性模型的构建过程非常耗时，随着LBSN的快速增长和不断演化，该模型的扩展性不佳；③CF模型不能有效地解决冷启动问题，难以为新用户或新位置提供推荐。

在大多情况下，用户兴趣内容、社会网络关联信息或位置特征等信息很难获取，仅具备用户的签到点及相应签到时间，这使得上述方法都很难适用。本文的研究为该方向进行了有效的补充，能在信息获取代价相对较小的前提下有效准确地预测用户签到位置。

7 结束语

本文提出基于向量自回归的位置转移演化算法对簇标记转移向量进行处理，挖掘用户位置转移随时间的动态变化规律。簇标记转移矩阵的提出，帮助描述在特定时刻该城市用户的位置转移情况，通过加入用户签到行为的时间信息，有效支持簇标记转移矩阵序列的生成。为验证模型的有效性，本文利用真实的Foursquare和Gowalla签到数据集进行实验，结果表明VAR比AR、SES和SMA表现得更好。本文将所提的LTE算法用于位置预测并与传统的算法进行对比，实验结果表明，本文算法具有更高的位置预测准确度。在未来的工作中，将针对具有相似位置转移的用户群体进行移动规律挖掘，从而提供更加精确的位置预测。