夹砂层土壤膜孔灌水分入渗规律数值模拟与试验验证

刘文光， 贾生海， 范严伟， 白贵林， 赵 彤

(1.甘肃农业大学 水利水电工程学院， 甘肃 兰州 730070； 2.兰州理工大学 能源与动力工程学院， 甘肃 兰州 730050)

1 研究背景

有机融合农业耕作措施与节水灌溉技术形成综合的节水技术体系，是节水农业关键技术的突破点，受到农业和土壤相关科研工作者的重视[1]。研究表明，夹砂层的存在可减小土壤水分下渗速率，提高上层土壤的水分含量[2-5]。基于夹砂土壤中水分的入渗特点，在黄土中设置砂层的耕作方法得到认可并应用[6-7]。

目前，夹砂土壤入渗机理研究主要是针对畦灌和沟灌灌水模式，取得了丰富的成果，为夹砂土壤应用提供了理论指导[8-13]。随着地膜覆盖技术的发展，膜孔灌逐渐发展起来，其利用地膜输水并通过作物孔和专用孔入渗进行灌溉，具有节水、保肥、灌水均匀度高等优点，在中国西北干旱半干旱区得到应用[14-15]。以往，膜孔入渗特性研究主要是针对均质土壤，对夹砂土壤入渗特性研究相对较少。面对新形势下农田不同节水灌溉技术，研究膜孔灌水模式下夹砂层土壤水分运动规律具有重要的现实意义，同时可为水资源高效利用提供理论依据。

随着计算机技术的发展，采用数值模拟方法进行土壤水分运动规律的研究成为趋势。由Simunek等[16]开发的SWMS软件被广泛用于模拟各种灌溉方式的土壤水分运动，并且取得了良好的效果。聂卫波等[17]采用SWMS-1D软件对均质土一维土壤入渗特性进行了数值模拟；范严伟等[18]利用SWMS-2D软件对层状土垂直一维入渗土壤水分运动规律进行了数值模拟；Li等[19]利用SWMS-2D模型软件对层状土壤膜孔入渗量进行了研究，但缺少必要的验证。

本文以室内试验为基础，针对土壤剖面存在砂质夹层的特点，基于Richard方程建立膜孔灌条件下夹砂层土壤水分运动数学模型，利用SWMS-2D软件求解，通过室内试验对模拟结果进行验证，分析数值模拟的夹砂土膜孔灌土壤水分运动规律的合理性及可靠性。以期借助数值模拟方法，进一步认识膜孔灌条件下夹砂土壤水分运动机理，为后期模拟分析土壤特性和灌水技术要素对夹砂土体中膜孔入渗特性的影响提供技术支撑。

2 材料与方法

2.1 室内试验

2.1.1 试验土样 供试壤土取自兰州市黄峪镇祁家营村苹果园内；砂土取自兰州市秦王川盆地。取土深度为5～60 cm，将土样带回实验室，经风干、碾压，过2 mm筛后制成试验土样，并采用激光粒度仪(MS2000)测量其颗粒级配。

参照国际制土壤分类标准，试验土样属于粉壤土和砂土，土样的基本物理特性见表1。

表1 试验土壤基本物理特性

2.1.2 试验方法 试验装置主要由马氏瓶和有机玻璃土箱组成，如图1所示，在土箱一角安装有膜孔室，并在侧面设置取土孔和底部设通气孔。将制备好的土样依照试验方案(见表2)，以粉壤土容重为1.33 g/cm3和砂土为1.55 g/cm3分层(5 cm)装入30 cm×30 cm×60 cm(长×宽×高)的有机玻璃土箱。试验中，用马氏瓶保持恒定水头供水，按已确定的时间间隔记录马氏瓶读数，并描湿润锋运移曲线，为防止水分蒸发在土箱上表面覆保鲜膜。试验结束后，从取土孔取土测定试验土体土壤含水量。

2.2 数学模型

2.2.1 基本方程 假设每层试验土壤为理想的均质且各向同性多孔介质，不考虑蒸发、温度以及土壤内部空气阻力对水分入渗的影响，在每层土壤具有相同的水分运动模型表达形式且有不同特性参数值的情况下，夹砂层土壤膜孔灌为充分供水条件下的三维入渗，可通过三维土壤水分运动基本方程的定解进行数值模拟。

(1)

式中：x为横向坐标，cm；y为纵向坐标，cm；z为垂向坐标，向上为正，cm；C(φm)为比水容重，cm-1；φm为基质势，cm；φ为总水势，cm；t为入渗时间，min；K(φm)为非饱和导水率，cm/min。

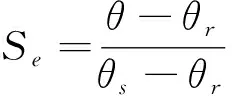
(2)

K(φm)=KsSe0.5[1-(1-Se1/m)m]2

(3)

式中：Se为土壤有效含水率，cm3/cm3；θ为土壤含水率，cm3/cm3；θr为土壤残余含水率，cm3/cm3；θs为土壤饱和含水率，cm3/cm3；α为与进气值成反比的经验参数，cm-1；n和m为影响土壤水分特征曲线形状的经验常数，m=1-1/n;Ks为土壤饱和导水率，cm/min。

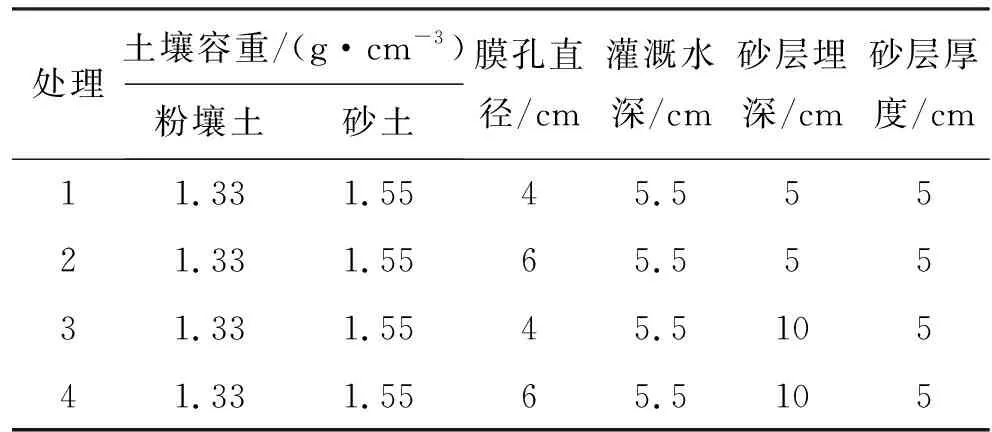
表2 夹砂层土壤膜孔灌试验方案

2.2.2 定解条件 因膜孔具有轴对称性，所以本试验可以简化为研究由1/4膜孔所控制的土壤水分入渗规律，简化后模型如图2所示，OBCD-O′B′C′D′表示试验土体，其中，EFGH-E′F′G′H′表示夹砂层。由此确定的定解条件为：

(1)初始条件。

φ=φ0,t=0, 0≤x≤d, 0≤y≤d,

-h≤z≤0

(4)

式中：φ0为土壤的初始总水势，cm；d为模拟土体的宽度，cm；h为模拟土体的深度，cm。

图1 试验装置图

(2)边界条件。在试验中，膜孔OAA′处水头保持恒定；采用保鲜膜将上边界AA′DCB覆盖，因此没有水分蒸发，所以为零通量面；由于膜孔的对称性，1/4膜孔边界面的OBB′O′和ODD′O′为零通量面；由于模拟土体体积较大，故可以认为边界面DCC′D′、BCC′B′和O′B′C′D′水分不会到达，即边界无水量交换，总水势会保持恒定。依上述分析，边界条件为：

边界OAA′：

(5)

边界AA′DCB：

(6)

边界OBB′O′：

y=0,t≥0

(7)

边界ODD′O′：

x=0,t≥0

(8)

边界DCC′D′：

φ=φ0, -h≤z≤0, 0≤x≤d,y=d,t≥0

(9)

边界BCC′B′：

φ=φ0, -h≤z≤0, 0≤y≤d,x=d,t≥0

(10)

边界O′B′C′D′：

φ=φ0, 0≤x≤d, 0≤y≤d,z=-h,t≥0

(11)

式中：h0为灌溉水深，cm；r为膜孔半径，cm；T为灌水时间，min。

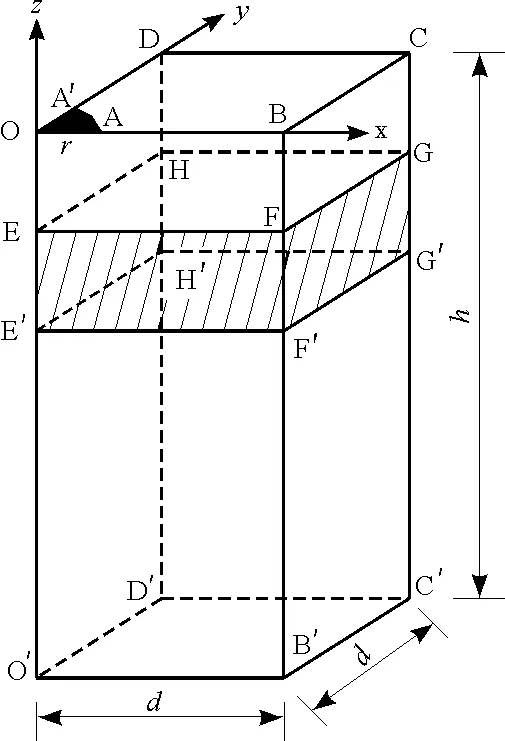
图2 计算简化图

2.2.3 数值求解方法 应用软件SWMS-2D对上述模型进行求解。将模拟土体剖面划分为方形计算单元，z轴方向间隔1 cm，x轴方向先密后疏，计算区域的深度为30 cm，半径为30 cm。试验土壤的VG模型参数见表3。

2.3 误差分析

采用以下4个指标，用于分析模拟值和实测值之间的误差，分别为：

(12)

(13)

(14)

(15)

式中：MAE为平均绝对误差；RMSE为均方根误差；PBIAS为偏差百分比；NSE为纳什效率系数；Yiobs为第i个实测值；Yisim第i个模拟值；Ymean为实测值的平均值；n为数据总个数。MAE、RMSE和PBIAS的数值越接近0，NSE的数值越靠近1，表示模拟值与实测值差值越小，两者吻合越好。

表3 试验土壤的Van Genuchten模型参数

3 结果分析

用SWMS-2D软件求解膜孔灌条件下夹砂层土壤水分运动数学方程，获得累积入渗量、湿润锋运移距离和土壤剖面含水量的模拟结果，将模拟结果与实测结果进行对比验证。

3.1 累积入渗量的数值模拟与验证

图3为不同处理下夹砂层土壤膜孔灌累积入渗量的模拟值与实测值的比较。

图3 累积入渗量的模拟值与实测值对比

由图3可以看出，膜孔直径对累积入渗量有影响，膜孔直径大者对应的累积入渗量较大，这是因为膜孔直径越大，水分进入土壤的通道越大，导致其累积入渗量越大；夹砂层埋深对累积入渗量有一定的影响，夹砂层的埋深大者对应的累积入渗量较大，主要是因为入渗水分达到砂-土界面向下运动的条件是砂土的进水吸力等于界面处粉壤土的基质势，夹砂层埋深小者的入渗水分先到达砂-土界面，随着入渗时间的增加，夹砂层埋深小者粉壤土的基质势增加程度较大，对应的水分入渗速率较慢，累积入渗量较小，从而表现出一定的减渗现象。

对累积入渗量的模拟值与实测值进行统计特征分析：MAE为0.05 L、RMSE为0.08 L、PBIAS为-0.81%、NSE为0.99。说明各时段数值模拟结果与实测值非常吻合，表明SWMS-2D能较好地模拟夹砂土壤膜孔灌累积入渗量的变化过程。个别处理实测值与模拟值相差较大，主要是为保持水头恒定，在试验开始前，需用凡士林将塑料薄膜粘贴于膜孔处，然后向膜孔室内注水至指定水位线，试验开始时再将薄膜去除，在这一操作过程中会产生水量损失(薄膜带出水)，从而造成开始时间段内的读数不准确；还有装土不均匀和读数误差等也会对试验数据的准确性有一定的影响。

3.2 湿润锋运移距离的模拟与验证

根据夹砂层土壤膜孔灌湿润锋运移的特殊性，分别进行不同处理下湿润锋水平向和垂直向运移距离的实测值与模拟值的对比分析，如图4所示。

分析图4中湿润锋的运动规律，可知，在其他条件相同时，膜孔直径大者水平向湿润锋运移距离较大，夹砂层埋深小者水平向湿润锋距离较大；每一种处理下水平向湿润锋运移距离明显大于垂直向，这是因为夹砂层的存在，在入渗水分到达砂-土交界面时，上层粉壤土的基质势小于夹砂层的进水吸力，只有当两者相等时水分才会开始下渗，于是水分会在上层土壤中蓄积并继续向水平方向运移，而垂直向则运移缓慢。

对湿润锋运移距离的模拟值与实测值进行统计特征分析，模拟值与实测值的MAE为0.28 cm、RMSE为0.36 cm、PBIAS为-1.56%、NSE为0.99。说明各时段数值模拟结果与实测值一致性良好，表明SWMS-2D能较好地模拟夹砂土壤膜孔灌各个方向湿润锋运移的变化过程。由于在试验中，只有当试验土体含水量达到一定量时，才可以观测到湿润锋，而且土壤中的禁锢气体产生的压力对入渗水流会有阻碍作用，所以，对湿润锋运移距离的模拟值进行适当减小。

3.3 土体剖面含水量模拟与验证

图5为不同处理下夹砂层土壤膜孔灌湿润体剖面含水量的模拟值与实测值的比较，实线为surfer软件利用模拟值绘制的土体剖面含水量等值线，圆点为实测值，原点0为膜孔中心，测点坐标为(x，0，z)，单位为cm。

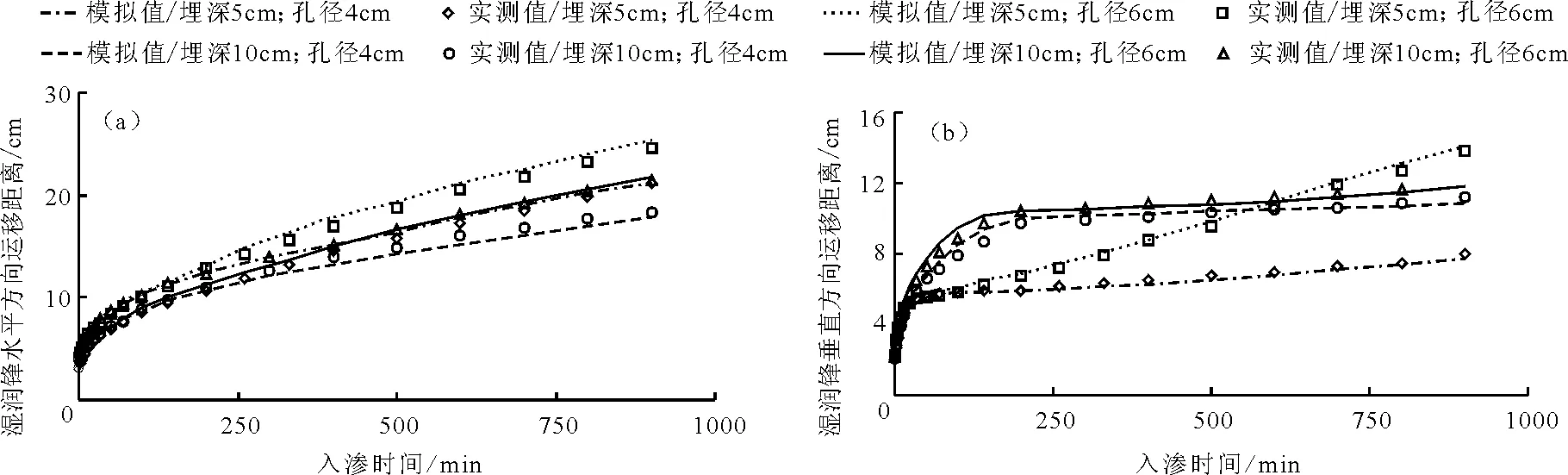
图4 湿润锋运移距离的模拟值与实测值对比

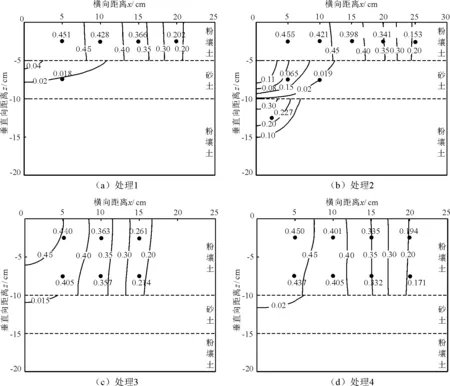
图5 湿润体剖面含水量的模拟值与实测值对比

分析图5中湿润体水分分布结果不难看出，湿润体的湿润锋面形状与均质土的半球体或半椭圆体不同，而是在粉壤土层与砂层的交界处出现了明显的不连续性，表现出了一定的阻水性。在其他条件相同时，膜孔直径对湿润体水分分布有影响，膜孔直径大者对应的湿润体体积较大；夹砂层埋深对湿润体水分分布有较大的影响，埋深小者入渗水分会穿过夹砂层到达下层土壤，水分会在每层土壤中重新分布，不与上层土壤的湿润锋面连续。

取相应点位的含水率模拟值与实测值进行统计特征分析，模拟值与实测值的MAE为0.11 cm3/cm3、RMSE为0.05 cm3/cm3、PBIAS为-6.36%、NSE为0.97。总体上，模型计算出来的湿润体含水量的模拟值与实测值相近，表明SWMS-2D能较好地模拟获得夹砂土壤膜孔灌湿润体水分分布状况。个别试验点土壤含水量误差较大，可能是由于土壤夯填不均匀，土钻取土有误差，且因取土量少造成称量不准确等误差产生。

4 结 论

(1)累积入渗量、湿润锋运移距离和湿润体剖面含水量的模拟值与实测值的MAE分别为0.05 L、0.28 cm和0.11 cm3/cm3；RMSE分别为0.08 L、0.36 cm和0.05 cm3/cm3，PBIAS分别为-0.81%、-1.56%和-6.36%；NSE分别为0.99、0.99和0.97，说明，数值模拟结果与试验结果具有较好的一致性。所建模型能较准确地反映夹砂层土壤膜孔灌水分运动规律。

(2)数值模拟结果与试验结果均表明，夹砂层具有一定的阻水和减渗作用，能够提高上层土壤的持水能力，而且使得不同处理下水平向湿润锋运移距离明显大于垂直向。膜孔直径和夹砂层埋深对累积入渗量、湿润锋运移距离和土体剖面含水量分布均有不同程度的影响：在其他条件相同时，膜孔直径和夹砂层的埋深大者对应的累积入渗量较大；膜孔直径大者和夹砂层埋深小者水平向湿润锋运移距离较大；膜孔直径大者对应的湿润体体积较大；夹砂层埋深对湿润体水分分布有较大的影响，会使入渗水分不连续分布。

(3)本文利用SWMS-2D软件对夹砂层土壤膜孔灌土壤水分入渗方程求解是可行的，模拟结果是可靠的。因此，SWMS-2D软件可为进一步研究不同夹砂层质地、入渗水头、初始含水率和夹砂层厚度等条件下的夹砂层土壤膜孔灌水分运动规律提供理论依据和技术手段。