半氢化石墨烯与单层氮化硼复合体系的电子结构和磁性的调控∗

高潭华 郑福昌 王晓春

1)(武夷学院机电工程学院,武夷山 354300)

2)(吉林大学原子与分子物理研究所,长春 130012)

1 引 言

自从实验上发现可以在富勒烯和石墨中产生自旋极化以来[1,2],轻元素磁性材料的研究受到了越来越多的关注.与传统基于过渡金属元素的d和f电子引起的磁性相比较,由sp电子的自旋极化引起的磁性有明显的优势,如长程耦合[3−5]等.特别是2004年发现石墨烯以来,人们在实验和理论上对由sp元素组成的二维材料的磁性进行了更加广泛深入的研究,得到了许多有趣的结果[6−10].Zhou等[6]根据石墨烯的氢化是可逆的性质,在理论上预测了从石墨烯到石墨烷再到半氢化的石墨烯,体系从金属性质转变为半导体性质,从非磁性转变为磁性,表面修饰为调控材料的相关性质提供了一个新的途径.Ma等[10]理论上预测并解释了在平面双轴应力作用下,二维半氟化BN、半氟化GaN以及半氟化石墨烯磁耦合性质的转换和调控.但由于石墨烯氢化是可逆的,自由悬挂的半氢化石墨烯是不稳定的[11,12].

由于二维h-BN具有稳定的结构、光滑干净平整的表面,因而成为良好的绝缘衬底[13−16].实验上已成功地在h-BN基底上生长出石墨烯,并且晶格失配度很小(约1.6%)[17−22].BN/Graphene界面体系也引起了广泛的关注,Giovannetti等[23]通过密度泛函理论预测双层BN/Graphene可以打开53 meV的带隙.陈庆玲等[24]研究了双层BN/Graphene的稳定性及其掺杂特性.Kharche和Nayak[25]采用第一性原理密度泛函理论和多体微扰论研究了在h-BN基底上的石墨烯和半氢化的石墨烯,得到了与实验一致的“在h-BN基底上的石墨烯带隙仍然为零”的结果,在h-BN基底上的半氢化石墨烯可以打开1 eV左右的带隙.这些研究都表明通过良好的衬底可以增加二维材料的稳定性,调控材料的电子性质,但是关于压力对这些二维材料性质的影响,都未进行研究.由于半氢化的石墨烯与单层的BN均为六角蜂窝结构,且它们的晶格常数非常接近(根据我们的计算,失配比仅为0.63%,失配比定义为:σ=(a2−a1)/a1其中a1,a2分别为半氢化石墨烯和单层BN的晶格常数),我们设想通过单层BN衬底以及在垂直于二维平面的方向上施加压力来调控半氢化石墨烯的电子性质和磁性.利用第一性原理计算详细讨论了半氢化石墨烯与单层氮化硼形成的界面体系(为了方便将体系记为H-Gra@BN),发现H-Gra@BN稳定的体系界面之间的相互作用很弱,但单层h-BN衬底对半氢化石墨烯各种性质的影响却非常显著的,利用这些特点可实现对该体系的电子结构和磁性进行调控.

2 计算方法与模型

计算采用基于密度泛函理论框架下的投影缀加波方法(projector augmented wave)[26,27]和VASP(vienna ab initio simulation package)程序包[28,29].由于半氢化石墨烯与单层BN之间缺乏强成键作用,范德瓦耳斯力的作用会很重要,在本工作中,所有H-Gra@BN体系的计算都采用了Grimme提出的DFT-D2方法[30].交换关联势采用广义梯度近似(generalized gradient approximation),采用Perdaw-Burke-Ernzerhof交换关联泛函[31].平面波截断动能为500 eV,系统总能量的收敛判据为10−5eV.布里渊区的积分采用Monkhorst-Pack方法[32]产生的7×7×3的以Γ为中心的特殊k网格点.二维的H-Gra@BN体系位于x-y平面内,在z-方向上使用了大于25 Å(1 Å=0.1 nm)的真空层来消除两个相邻体系之间的相互作用.所有计算采用2×2超胞模型.在结构优化过程中,各结构中的所有原子都进行了充分的弛豫,使得超原胞内所有的原子在 x,y,z方向上的Hellmann-Feynman力[33]均小于0.01 eV/Å.计算中,C,H,B和N原子的价电子分别采用:2s22p2,1s1,2s22p1和2s22p3.分别通过对半氢化石墨烯和单层BN的计算,对该方法的精确度进行了检测,得到的晶格常数为2.528 Å,C—H键长为1.171 Å,C—C键长为1.483 Å以及铁磁性性质都与文献[6]的结果基本一致.对于单层BN计算的结果为:晶格常数为:2.512 Å,B—N键长为1.450 Å及电子性质与文献的结果也一致.

图1 六种构型H-Gra@BN的顶视图(左)和侧视图(右),图中几何图形为计算采用的超原胞(为2×2超胞模型)Fig.1.(a)–(f)The six optimized structures of H-Gra@BN in top view(left)and side view(right).The rhombus lines show one supercell.

3 结果与讨论

3.1 体系的结构稳定性

很多单层材料都是依附于基底生长的[34],我们只考虑石墨烯一面氢化,而另一面不进行氢化的情况.为了确定H-Gra@BN体系最稳定的结构和磁耦合方式,我们采用了2×2超胞模型进行模拟,考虑了AA-B,AA-N,AB-B,ABB-H,AB-N和AB-N-H六种异质结层间对接的构型,分别对六种构型的体系都进行了非磁、铁磁和反铁磁几何优化后,得到稳定的几何结构如图1所示,并计算体系的形成能(形成能定义为:

Ead=(Etotal−EH-Gra−Emono-BN)/N,其中Etotal为H-Gra@BN体系的总能,EH-Gra和Emono-BN分别为H-Gra和单层BN的总能,N为所有原子的总数),结果列于表1.其中构型AB-B铁磁性的形成能最低,最为稳定,H-Gra@BN体系的厚度h也最小(h定义为最稳定的H-Gra@BN体系最上层原子H与最底层原子N之间的距离),所有构型的形成能均为负值.形成能数值较小,表明层间存在一定的结合作用,可形成较为稳定的异质结构.但其他构型的形成能相较于构型AB-B差异很小(不超过12 meV/atom)且均为铁磁性,晶格常数(a)、原子间的键长(dC—H,dB—N,dC—C)以及两碳原子层间距(∆)等参数都基本相同,说明层间的结合作用与层间的对接方式并没有太大的关系,H-Gra与单层BN之间的作用应该为范德瓦耳斯结合作用.为了方便,以下均以构型AB-B为例进行讨论.

表1 单层BN,H-Gra以及六种构型的H-Gra@BN的几何结构参数(单位 Å)(其中:a,dC—H,dB—N,dC—C,h,∆分别代表二维材料的晶格常数、碳氢键的键长、硼氮键的健长、碳碳键的健长、H原子层与N原子层之间的层间距以及两碳原子层之间的层间距;Ef(单位meV)代表体系的每个原子的平均形成能;NM,FM,AFM分别代表非自旋极化态、铁磁态和反铁磁态的相对能量(单位:meV);除了单层BN为非自旋极化态外,所有最稳定的平衡态均为铁磁态)Table 1.Structural parameters calculated for monolayer BN,H-Gra and six configurations of H-Gra@BN(in Å):a(lattice constant),dC—H(C—H bond length),dB—N(B—N bond length),dC—C(C—C bond length),h(distance between of H and N atomic layer),and∆(buckling distance of carbon atomic layer);Ef(meV)indicates the average forming energy of each atom in system;NM,FM,and AFM represent nonmagnetic,ferromagnetic and antiferromagnetic state of relative energy(unit:meV)respectively.All of the most stable equilibrium state are ferromagnetic states except for monolayer BN is nonmagnetic state.

3.2H-Gra@BN的电子结构和磁性性质

为了探究H-Gra@BN体系的自旋电子性质,我们计算了体系最稳定结构时的自旋极化的能带结构和总态密度,结果如图2所示,发现该材料为磁性间接带隙半导体,能带为非对称的自旋向下和向上的两个通道,其中上下自旋的导带底都位于Γ点,价带顶都位于Γ点与K点之间,均呈现为间接带隙的结构,自旋向下的价带在费米能级之下,带隙值为1.798 eV,自旋向上的带隙值为 3.097 eV.进一步讨论H-Gra@BN体系的磁性质,发现体系中未被氢化的C原子的磁矩大约为1µB,计算了铁磁性(FM)、反铁磁性(AFM)以及非磁性(NM)三种磁性结构的基态能量,发现铁磁性耦合的是最稳定的(如表1所列).图3给出了自旋极化电荷密度的分布,图中也清楚地表明未氢化C(C2)原子存在明显的自旋极化,而其他原子上的自旋极化几乎为零.这些结果与文献[6]中无衬底的半氢化石墨烯的结果一致,说明单层BN衬底并不会改变半氢化石墨烯的奇异物理性质.

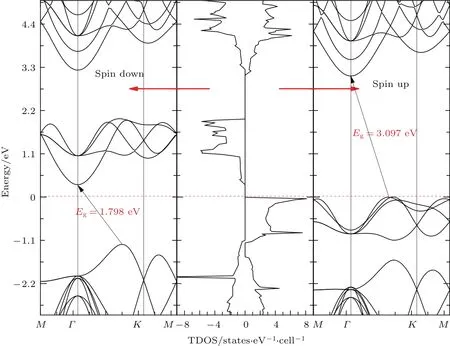
图2 AB-B构型的H-Gra@BN体系的能带结构和总态密度,图中的红色虚线为费米能级Fig.2.Calculated band structures and total density of states(TDOS)for the AB-B configuration of H-Gra@BN,the Fermi energy is set at 0 eV.

图3 H-Gra@BN体系最稳态的极化电荷密度三维等高图,其中等高面间隔为0.25 e/Å3Fig.3. The spin-polarized charge density isosurface(isosurface value 0.25 e/Å3)of the most stable H-Gra@BN.

图4给出了半氢化石墨烯与单层BN复合体系的各原子的分波态密度图,通过对原子分波态(PDOS)的分析,可深入了解自旋极化态的轨道贡献.图4从上至下分别表示H-Gra@BN体系中C2,C1(氢化的C原子),H,B和N原子各电子轨道的分波态密度,在费米能级附近对自旋向上有贡献的主要来源于C2原子价带的pz态,而H原子价带的s态以及N原子价带的pz态也有少量的贡献;费米能级附近自旋向下有贡献的主要也是C2原子导带的pz态,其余原子的贡献非常小,这与之前极化电荷密度的分析是一致的.

图4 H-Gra@BN体系各原子的分波态密度,红色虚线代表费米能级Fig.4.PDOS of atoms in H-Gra@BN.The Fermi energy is set at 0 eV.

3.3 应力对H-Gra@BN体系电子结构和磁性的调控

应力作用在纳米体系中是非常重要的,之前的研究[9,23]已经证实了应力可以很有效地调控纳米体系的电子性质.关于施加压应力对H-Gra@BN复合体系性质进行调控,由前面的分析可知:在平衡状态下,半氢化石墨烯与单层BN之间是较弱的范德瓦耳斯力作用,因此在体系的z方向应该是很容易拉伸或压缩的.我们以图1(c)AB-B构型为例,对H-Gra@BN复合体系在z方向施加压应力,施加的应力与应变存在对应关系,因此被定义为σ=∆h/h,其中∆h为h的变化量.应力施加范围为0→ −12.12%,施加应力的方式为首先将体系的层间距从h变化为h+∆h,然后进行几何优化.具体的计算模拟为:分别固定最上层的H原子和最下层的N原子z方向的坐标,其他原子以及H和N原子的其他方向都进行弛豫.我们计算了H-Gra@BN体系的形成能,得到体系的形成能从−40 meV/atom变化为−7.42 meV/atom,形成能保持为负值,因此我们断定施加压应力的过程体系能够稳定地存在.图5给出了应力施加过程中HGra@BN体系的总态密度,图5(a)—(d)分别表示z方向应变为0%,−5.82%(∆h= −0.25 Å),−1.48%(∆h= −0.45 Å) 和 11.65%(∆h= −0.5 Å)时复合体系的总态密度,发现上自旋通道的价带顶(VBM)当压力增加到一定值后,随着压力的增加逐渐移至Fermi能级之上,而导带底(CBM)则基本没有变化;下自旋通道则相反,随着压力的增加VBM基本没有变化,CBM则逐渐向低能移动,最后移至Fermi能级之下.H-Gra@BN复合体系的电子性质在压力的作用下从磁性半导体转变为半金属,最后转变为非磁性金属.图6显示了不同垂直压缩应变值下的能带结构,可以看出随着层间距离的减小,层间化学相互作用的增加,当应变大于−10.48%(∆h= −0.45 Å)时,下自旋通道的VBM VDH向下移动,而CBM ΓDL则从高对称的Γ位置转变为Γ与K之间的TDL点,并且穿过Fermi能级,同时上自旋通道的VBM也穿过Fermi能级,发生了由磁性半导体到金属的转变.这一结果可通过对电荷的重新分布的计算得到进一步的支持,对H-Gra@BN双层系统的总电荷密度与孤立的H-Gra和BN单层电荷密度差分计算(即∆ρ= ρH-Gra@BN−ρH-Gra−ρBN)得到图7(a)—(d).电荷的再分布主要发生在两层层间的C2-B原子之间,当两层原子由于应变靠近时,C2与B之间的电子密度向两原子中间聚积,它们之间的作用表现为明显的共价键特征.当应变为−11.65%(∆h= −0.5 Å)时,在H,C2和N原子周围呈现明显的电荷分布,此时的材料转变为金属性.图8系统地展示了AB-B构型的H-Gra@BN体系在自旋向上和自旋向下的导电性、带隙宽度以及磁矩随层间距的变化趋势,材料的这一特点可应用在对应力敏感的纳米电子器件以及智能建筑材料等领域.

图5 在不同的应变值时的总态密度0%,−5.82%(∆h= −0.25 Å),−10.48%(∆h= −0.45 Å)和 −11.65%(∆h=−0.5 Å),费米能级位于0 eV处Fig.5.TDOS of H-Gra@BN in different strain values,i.e.,0%,−5.82%(∆h= −0.25 Å),−10.48%(∆h= −0.45 Å)and −1.65%(∆h= −0.5 Å).The Fermi energy is set at 0 eV.

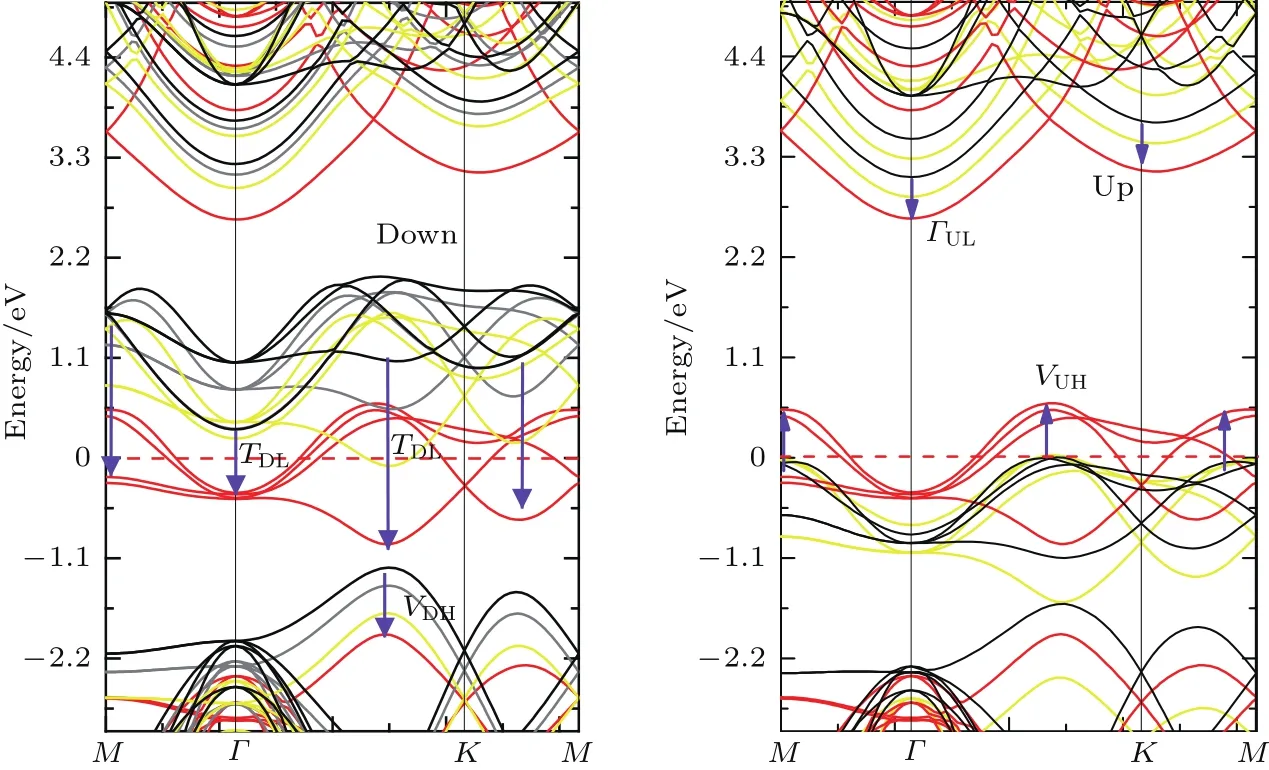
图6 不同的应变值用不同颜色的能带结构表示即黑色(0%),灰色(−5.82%(∆h= −0.25 Å)),黄色(−10.48%(∆h= −0.45 Å)),红色(−11.65%(∆h= −0.5 Å)),费米能级位于0 eV处Fig.6.Computed band structures of H-Gra@BN under compressive strain along z direction.The bands with different colors denote the band structures under different strain,i.e.,black(0%),gray(−5.82%(∆h= −0.25 Å)),yellow(−10.48%(∆h= −0.45 Å)),and red(−10.48%(∆h= −0.45 Å)).The Fermi energy is set at 0 eV.

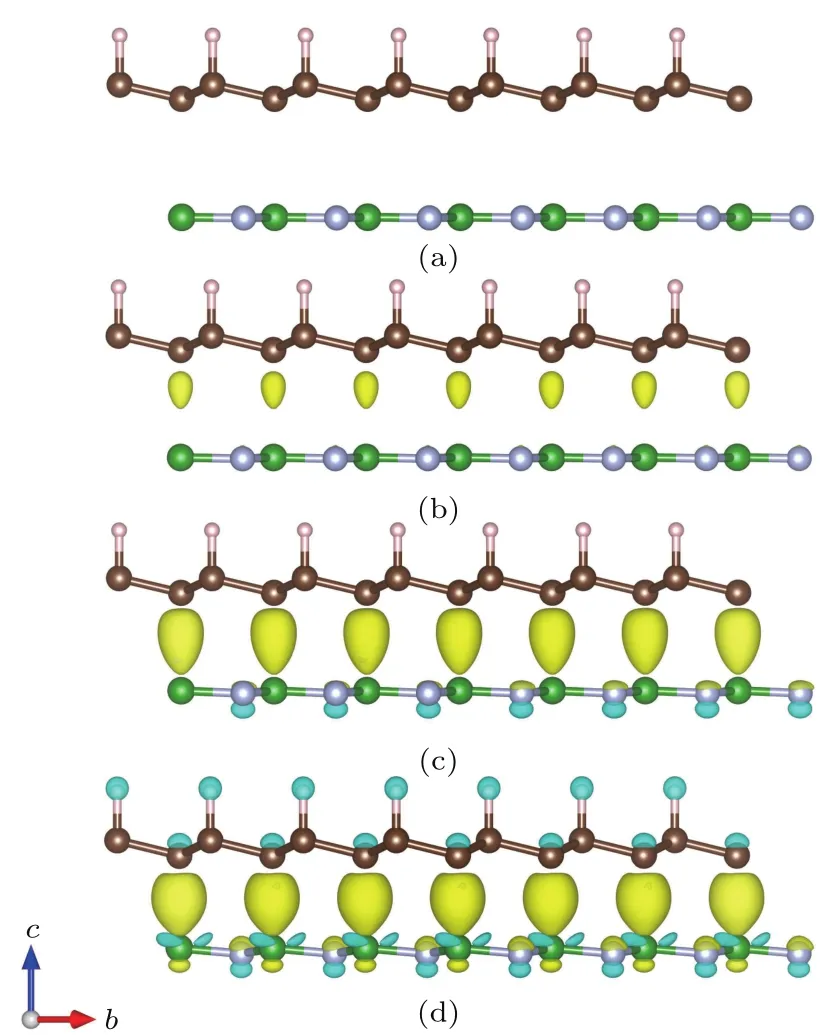
图7 不同应变值时的差分电荷密度三维等高面图(a)0%;(b)−5.82%(∆h= −0.25 Å);(c)−10.48%(∆h= −0.45 Å);(d)−11.65%(∆h= −0.5 Å),图中等高面间隔为0.02 e/Å3Fig.7.The difference of 3D charge density under different strain,i.e(a)0%;(b)−5.82%(∆h= −0.25 Å);(c)−10.48%(∆h= −0.45 Å);(d)−11.65%(∆h=−0.5 Å).The isosurface value 0.02 e/ Å3.

图8 AB-B构型的H-Gra@BN体系的导电性以及带隙宽度随层间距的变化Fig.8.The conductivity and bandgap of H-gra@BN in AB-B configuration change with the distance of interlayer spacing.

4 结 论

采用密度泛函理论第一性原理的PBE-D2方法对半氢化石墨烯与单层BN组成的复合体系(HGra@BN)结构的稳定性、能带结构和电子态密度等进行了系统的研究.计算结果表明:最稳定的H-Gra@BN体系为AB-B构型,是铁磁性半导体,上、下自旋的带隙分别为3.097和1.798 eV,每个物理学原胞约有1µB稳定的磁矩,该磁矩主要来源于未氢化的C2原子.由于该体系的H-Gra原子层与BN原子层之间的作用是范德瓦耳斯力,在z方向对该体系施加压力,实验上很容易实现.计算表明:当z方向的应变范围为0→−12.12%时,H-Gra@BN体系的电子性质由磁性半导体转变为半金属再转变为非磁性金属.本文预测了一种方便通过应力调控电子结构和磁性的具有应用前景的新型材料,有望用在对应力敏感的纳米电子器件以及智能建筑材料等领域.