融合社会标签与信任关系的社会网络推荐方法

胡 云 张 舒 李 慧 施 珺 仲兆满

(1.南京中医药大学信息技术学院,南京,210023； 2.淮海工学院商学院, 连云港,222005； 3.淮海工学院计算机工程学院,连云港,222005； 4. 江苏省海洋资源开发研究院, 连云港,222005)

引 言

伴随着社交网络的盛行，在线用户生成的信息呈指数型增长，社会语义信息的分析对于许多Web应用程序变得越来越重要,然而用户冷启动问题导致的用户-项目矩阵数据稀疏性等问题严重影响了推荐质量。现有的推荐方法均未能很好地处理具有极少评分项的用户推荐。目前推荐系统与各种社会背景信息相关联，包括用户的社会信任网络、用户标签[1-3]或与项目相关的标签信息等[4-5]。

社交标签可以通过从新的方向反映用户对网络资源的偏好来描述用户选择的类型，即社会化标签反映了用户感兴趣的一些主题，可以利用一些主题偏好比如标签的使用来推断用户的兴趣方向。目前大量关于社会标签系统的研究调查[6-10]已经证实了标签可以很精准地代表用户对网页内容的判断及喜好，也可以很好地对资源进行描述。Heymann等[6]对社会化标签预测进行了研究，发现基于标签的关联规则可以产生非常精确的标签预测；Ramage等[11]采用标签作为一种辅助数据源应用于页面文本和锚文本，用来提高网页自动聚类；Wu等[12]在带有权重的标签社会网中应用了基于扩散的推荐方法来提高推荐系统的精度，然而对是否可以利用社会标签信息来帮助提高推荐质量的研究甚少。因与以往研究工作不同，本文的研究将社会标签信息与信任度相融合来提高社会化推荐的质量，从而有效地解决了推荐系统中的冷启动问题。

信任网络是指由社会网络内部所有存在信任关系的用户所共同构成的一种网络结构。现在，进行社会网络推荐的算法有很多，它们主要以信任关系为基础，但大多数还是偏向于如何进行准确的信任度计算和信任模型的推理。如对用户进行推荐预测时可以使用多种相似度度量方法的线性组合[13];基于用户信任关系矩阵的概率分解和传统评分矩阵的概率分解提出了一种新的推荐方法，该方法基于受限关系和概率分解矩阵[14];当对用户的兴趣进行建模时，进一步通过辨别与目标用户有相同爱好的朋友来解决恢复信任度的过程[15];通过合并多个目标函数，在矩阵分解的框架下解决问题[16]。

为了有效解决社会网络推荐中的冷启动问题，让社会网络推荐变得更加高效，本文提出了一种基于社会标签与信任关系的社交网络推荐方法(Tag-based and trust-based recommendation，TTR)，该方法结合社交标签和信任度的社会化推荐方法，在基于概率因式分析的基础上集成了社会信任关系、项目标签信息以及用户项目评分矩阵。将这些维度不同的数据资源通过公共的用户潜在特征空间(或项目潜在特征空间)进行相连接，利用概率矩阵因式分解技术实现降维，从而在获得低维度的用户及项目潜在特征空间的基础上实现高效的社会化推荐。在Epinions和Movielens数据集上的实验结果表明，与现有的基于信任度的社会化推荐及社会标签推荐算法相比，TTR算法的推荐性能更加优越，特别是当用户的评分数据量非常少时，其优势就变得很明显。另外，通过算法的复杂度分析，显示该算法适用于非常大的数据集，因为算法的复杂性和观测数据的数量之间存在线性关系。

1 信任矩阵分解模型

信任矩阵分解的基本思想就是对社会网络的信任关系进行分析，从而获得两个分别表示用户和信任关系的低维潜在特征矩阵。通过以上处理，能够完成评分矩阵R向用户特征矩阵U和项目特征矩阵V的转换，这些特征是描述用户和推荐对象的重要因素。为了进一步发掘出潜藏在信任关系之后的用户特征，通过信任关系来提升推荐的准确度，使用信任关系矩阵对目标函数进行限制，将社会关系矩阵和用户评分矩阵在共享用户特征空间上进行联合概率分解，挖掘出评分相近又具有相同兴趣嗜好的信任用户成为邻居用户产生推荐，与之对应的概率图模型如图1所示。用户信任关系矩阵B可用用户特征矩阵U和信任特征矩阵Q的内积表示；用户-项目评分矩阵R可用用户特征矩阵U和项目特征矩阵V的内积表示。

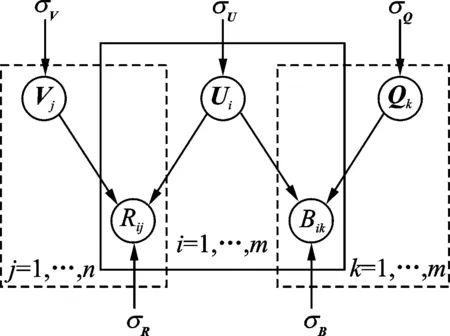
图1 基于信任推荐的概率图模型 Fig．1 Probabilistic graphical model based on trust recommendation

假设在R中包含m个用户和n个项目，Rij则表示用户ui对项目vj的评分，分解得到的用户特征矩阵用U∈Rl×m表示，用Q∈Rl×m表示分解得到的信任关系特征矩阵，用l表示用户特征个数，列向量Ui,Qj分别表示用户ui和信任矩阵B所对应的潜在特征向量。为了使预测评分UTQ与用户信任关系矩阵B的误差最小，定义信任关系矩阵B的条件概率分布为

(1)

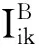
(2)

(3)

通过贝叶斯推荐可得

(4)

将信任矩阵B代入式(4)，可得

(5)

式(5)利用用户自己评论的信息与信任矩阵对用户和信任的潜在特征进行估算，具体的求解过程与标签模型相似，在此就不再展开。

2 融合标签与信任关系的推荐模型

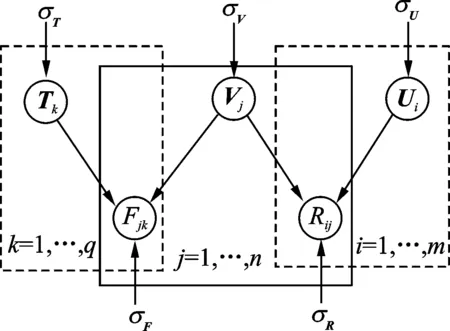
图2 基于标签推荐的概率图模型Fig．2 Probabilistic graphical model based on tag recommendation

基于如何利用用户的社会信任关系进行推荐的总体框架，可以很容易地扩展到融合用户项目评分矩阵与社会标签推荐模型上来。与用户评分相似，具有相似标签的项目信息同样也可以作为推荐的重要来源，因此本节利用相同的因式分解技术对用户项目评分与项目标签进行分解。通过共享的项目特征将用户的矩阵与项目标签信息进行联合，得到如图2所示的基于标签推荐的概率图模型。其中T表示每个标签的潜在特征，Fjk表示标签，其值为项目vj被标签tk标记的次数。用户潜在特征空间从评分与标签角度反映了用户的喜好，而项目潜在特征空间也可以由项目所收到的评分与标签信息来体现。

与信任矩阵分解模型相似，可以得到

(6)

联合用户评分矩阵与项目标签矩阵分解的后验概率值满足

(7)

式中ε为与参数无关的常数。当式(7)取最大值时，可知项目评分矩阵与标签矩阵最小偏差值可分解相对应的用户特征矩阵、项目特征矩阵和标签特征矩阵。将式(7)简化成为式(8)，可将解决最大值的问题转换为解决相对应的式(8)的最小值问题。

(8)

(9)

式中：g′(x)为函数g(x)的导数，即g′(x)=exp(x)/(1+exp(x))2；为了减少算法的复杂度，令λU=λV=λT；参数λT用于控制将多少项目的标签信息融入到推荐模型中。算法对于U,V和T的学习方法如下：首先随机初始化U,V和T的取值，然后根据梯度值迭代更新矩阵U,V和T，直至目标函数达到收敛。

算法主要的计算代价在于目标函数L和在矩阵U,V和T的梯度学习上。由于用户-项目评分矩阵R和标签矩阵F都是稀疏矩阵，假设R和F中的非零元素数目分别为ρR和ρF，则目标函数L的计算复杂度为O(ρRl+ρFl)；式(9)中梯度∂L/∂Ui，∂L/∂Vj和∂L/∂Tk的计算复杂度分别为O(ρRl+ρFl)，O(ρRl)和O(ρFl)。因此算法运行一次总的计算复杂度为O(ρRl+ρFl)，这也说明了算法的复杂度与观测数据成线性关系。

3 实验与结果分析

3.1 数据集与评价指标

本文研究的社会信任关系类型是有向的，所以选择两个公开的产品评论网站中的数据作为此次实验的数据集：Epinions和MovieLens数据集。在该网站上的用户不仅可以对不同的产品进行评分，还可以对产品进行评论。另外，用户还可以对其他用户对该产品写下的评论进行评价，并将可信用户添加到“信任列表”里。MovieLens数据集拥有众多的社会标签信息，包含了10 000 054条评分数据和95 580条标记数据，是由71 567名用户对10 681部电影标注产生的。本节中使用其中的10M/100M数据集进行测试。两个数据集的统计数据如表1所示。

MovieLens 10M/100M数据相聚随机选择80%作为训练集，20%作为测试集。每次实验验证都是独立的运行几次，最终将其结果取平均值。实验采用平均绝对误差(Mean absolute error，MAE)和均方根误差(Root mean square error，RMSE)作为系统评估指标，对各个推荐系统的性能进行对比。

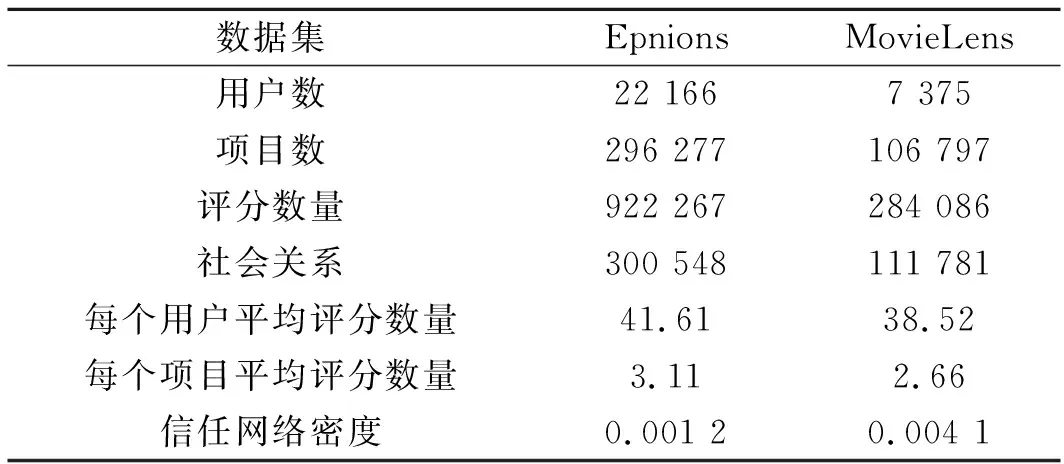
表1 Epinions和MovieLens数据集的统计数据

MAE为全部单个观测值和算术平均值的偏差的绝对值，其大小与推荐性能成反比，即其值越小，则说明其推荐性能越好，定义为

(10)

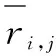
RMSE表示观测值与真值偏差的平方与观测次数N比值的平方根，其大小也与推荐性能成反比，即其值越小，其推荐性能越好，定义为

(11)

3.2 参数的影响实验

在TTR推荐模型中，融入用户-项目评分矩阵和标签信息之间的比例大小由参数λT来控制。如果λT取值为0，表示它的推荐只对用户评分矩阵信息依靠来进行；如果λT取无穷大时，表示推荐模型只对项目所被标注的标签信息依赖进行用户喜好的预测。只有联合订阅者自身的评价信息和项目标签信息，推荐效果才最有利。

实验环境的参数为：用户特征矩阵的维度L=10，λU=λV=0.1。训练集比例分别选取10%，30%，50%和80%，图3给出了当用户特征矩阵维度L=10时对MAE与RMSE在不同比例训练集下的实验结果。由图3可知，参数λT对算法的推荐性能会产生重要影响，也验证了用户评分矩阵与社会标签的融合将有助于提升推荐性能。随着λT的增大，推荐精准度逐渐提高，但当λT值继续增大时，推荐性能反而随之降低。由图可知，当参数λT的取值为20时，MAE的值最低，算法推荐性能最好，因此将参数λT的取值设为20。

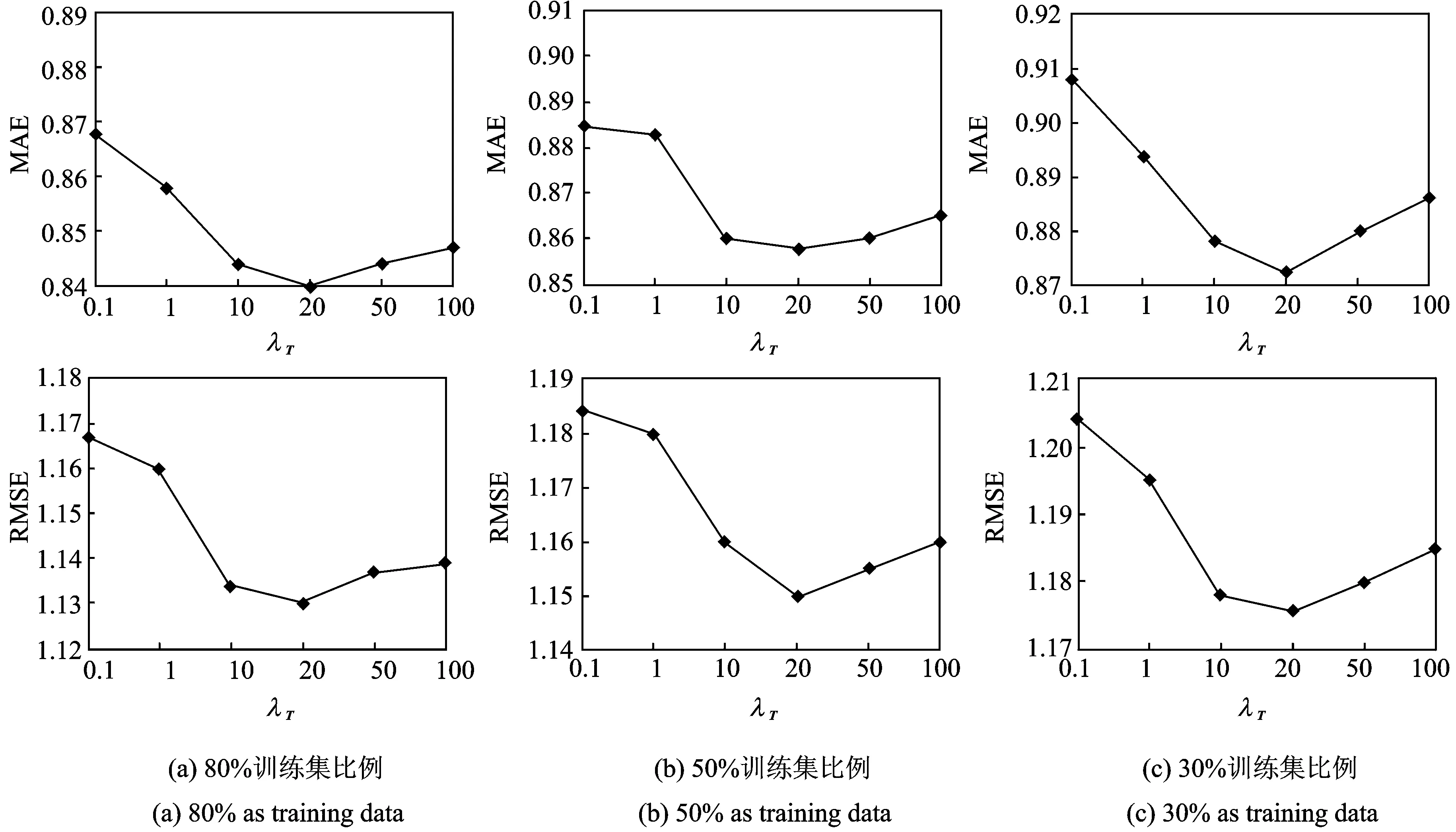
图3 不同训练集比例下参数λT对算法性能的影响实验(L=10)Fig．3 Influence of parameter λT to algorithm performance under different training set ratios

3.3 算法性能对比实验

通过与以下几种算法的对比实验来对本文提出的TTR算法进行验证。

(1)UserMean：使用每个用户为每个项目所打分的平均值来预测用户没有得分项。

(2)ItemMean：使用每个用户为每个项目所打分的平均值来预测用户的评分数据。

(3)概率矩阵分解 (Probabilistic matrix factorization，PMF)[17]：是由Salakhutdinov等提出的一种基于概率的矩阵分解技术。

(4)非负矩阵分解( Non-negative matrix factorization，NMF)[18]：是由Lee等提出的一种只使用评价矩阵信息的推荐方法。

(5)奇异值分解(Singular value decomposition,SVD)[19]：通过有效处理评分矩阵中的缺失项来提高推荐系统的性能。

(6)社会网络矩阵分解(Social matrix factorization, SocialMF)[20]：利用用户兴趣爱好传播进行建模的一种推荐方法，也是本文的研究基础之一。可是该算法没有考虑不可信节点影响信任建模的情况，对用户和好友之间的偏好差异没有限制。

实验中使用的参数设置如下：λT=20；用户特征矩阵的维度L=10；λU=λV=0.1。本文提出的TTR算法最大的贡献是在传统社会推荐算法的基础上融入了社会标签信息，优化了项目属性的构建。为了更进一步验证项目标签比例对算法性能的影响，首先将训练集中按照项目所被标注的标签数量划分为5组，分别是项目标签数量为“0”， “1-5”, “6-10”, “11-20”,“> 21”，取TTR算法在不同训练集上对不同项目标签数量下，以MAE和RMSE作为评测标准进行推荐效果的对比，实验结果如图4所示。

图4 推荐算法在不同训练集比例下的性能比较Fig．4 Performance comparison of the recommendation algorithms under different training set ratios

由图4可知，本文提出的TTR算法由于考虑了项目标签的信息，因此在推荐精度上有显著提高。随着项目被标注的标签信息增大，推荐系统的质量首先显著提升，但随着标签信息量继续增加至20以上，系统性能趋于稳定。这个结果也是合理的，因为随着标签信息的增加，项目属性被描述得越准确；但当项目标签过多时，将会导致项目描述信息的冗余，最终实验选择项目标签数量为20。

表2给出了所有算法在Epnions和MovieLens数据集上的对比实验结果。实验分别在潜在特征向量维度为5，10和20三种取值下进行验证。从对比结果可以看出，本文提出的TTR算法在两个数据集上的所有维度取值下性能均优于其他算法。

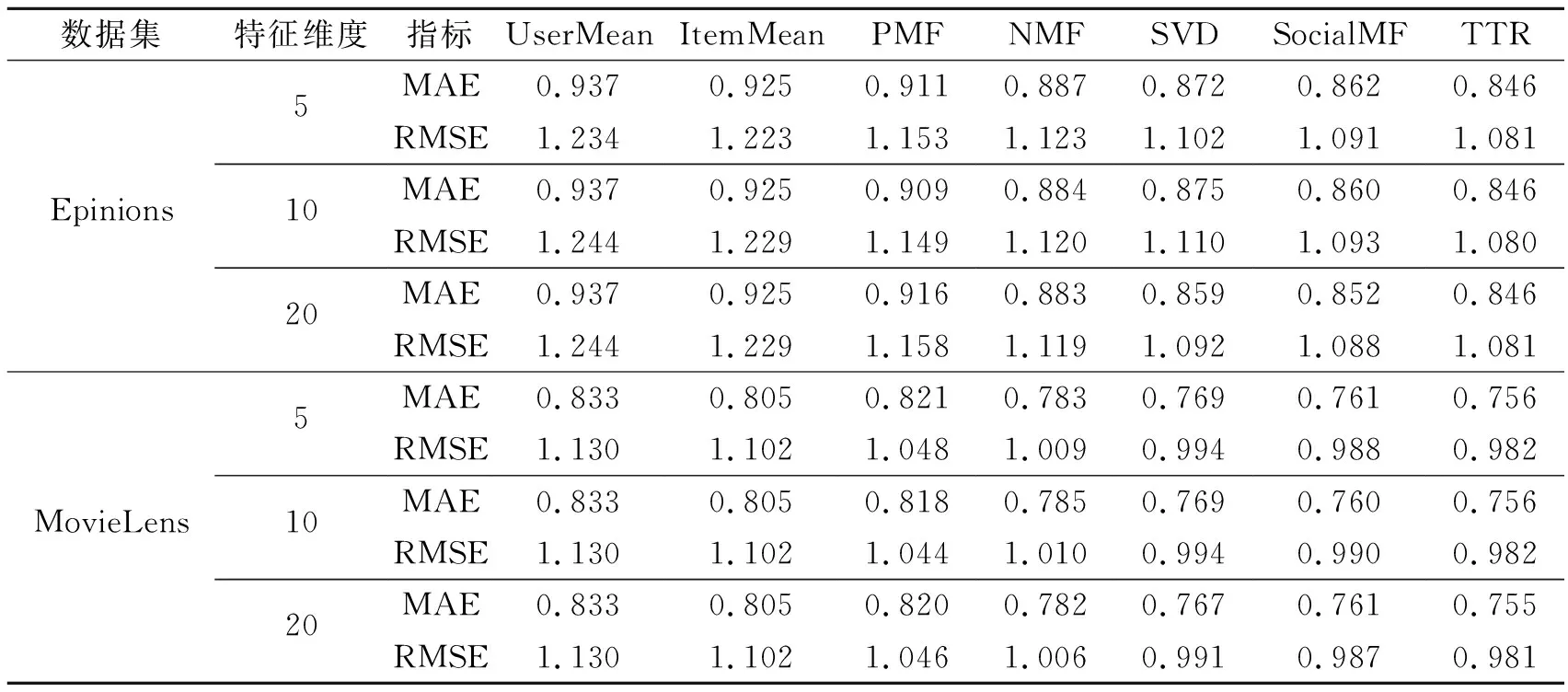
表2 各种推荐算法在不同数据集上的性能比较

4 结束语

推荐系统主要以用户历史评分信息为基础，对其喜好进行预测，但是如果当新用户没有任何评分数据或信任关系信息时，推荐系统就无法进行有效的预测，因此冷启动用户是影响推荐系统性能高低的关键因素。社会网络中包含着丰富的标签信息，可以被用于提升社会化推荐的精准度。本文研究的主要贡献在于将社会标签信息与信任关系信息相结合，提出了一种融合社会标签与信任关系的社会网络推荐算法。该算法最大的优势在于对新用户的评分进行了预处理，并且在构建项目属性时加入了项目被标注的标签信息，从而能在一定程度上提高推荐系统的准确性。实验结果表明，将用户信任关系与项目标签信息相融合的推荐方法在平均绝对误差和均方根误差指标上较其他推荐方法有大幅度的提高，特别是对冷启动用户较多的信任网络效果更加明显。由于社会标签信息和信任关系会随着用户兴趣的迁移会不断变化，因此下一步的研究方向是对社会标签及信任关系的动态演化进行分析研究，从而实现更加高效的实时推荐。