Self-consistent of a Modification Method Based on Membrane Model with Minimal Length Considered∗
Hao Tang(唐浩),Cheng-Yi Sun(孙成一),Bin Wu(吴滨), Yu Song(宋宇),and Rui-Hong Yue(岳瑞宏)
1School of Science,Xijing University,Xi’an 710123,China
2Institute of Modern Physics,Northwest University,Xi’an 710069,China
3School of Physics,Northwest University,Xi’an 710069,China
4Shaanxi Key Laboratory for Theoretical Physics Frontiers,Northwest University,Xi’an 710069,China
5College of Physical and Technology,Yangzhou University,Yangzhou 225009,China
AbstractBy adopting a result from generalized uncertainty principles(GUP),we modify the inner bound of the membrane model to a physical fixed value and get the cut-o ff s naturally rather than by hand,which are both in brickwall model and membrane model,and the semi-classical quantization condition could always be valid as well.We also calculate the entropies of Schwarzschild-de Sitter black hole and find the GUP we choose qualitatively shows that the requirement of mass in this method is the same with the natural requirement of the Schwarzschild-de Sitter black hole,which means the method might be self-consistent.
Key words:entropy,black hole,generalized uncertainty principle,brick-wall model,membrane model
1 Introduction
Bekenstein[1]and Hawking[2]proposed that a black hole should have entropy,and showed that the entropy of a black hole is related to its area of the event horizon.Explicitly,the relation is S=A/4,where S is the entropy,and A is the area of the black hole’s event horizon.This is called the Bekenstein-Hawking entropy.After that,the entropy of black holes have been studied for decades.People have developed many methods to calculate the entropy of black holes.The results mainly support the idea that the entropy of a black hole is directly proportional to it’s area of the event horizon.One of these called the brick-wall model[3]is widely used,which is brought out by G’t Hooft on 1985.This model believes that the entropy of a black hole is the entropy of the quantum gas in thermal equilibrium exists between the external fields and the black hole horizon in a spatial region,which is called the “brick-wall”.With this method,people have obtained many useful results.[4−10]This model gives us a clearer and easier method for calculating the entropy of a black hole and gives acceptable explanations.Normally,the formulation of the entropy contains many parts.One of the parts contributes the main entropy component while others are just small corrections.
Liu and Zhao[11]modified this model.They believe that the main part of the entropy may come from a very thin wall named the membrane[12−13](or called the film[14]),which is called the membrane model.This model is more simple,some papers had studied the entropy with this model[12−16]and got some beautiful results.Mathematically,this model assumed that the thickness of the wall could reduce to zero.Thus,the entropy of a black hole could be taken as the entropy of a two-dimensional membrane.This view is very charming,and could give a nice result.But,physically,if the thickness of the wall reduces to zero,the semi-classical quantization,which is used in the membrane model might be invalid.
However,both the brick-wall model and the membrane model contain the disadvantages that there need a cuto fftaken by hand in order to satisfy the result of the Bekenstein-Hawking entropy.Moreover,the physical picture is not quite clear.
To solve this puzzle,we modify the membrane model.Since the thickness of the wall should not reduce to zero,we could change the lower limit to a finite value.This value should have its own physical meaning.If we change this limitation,the calculation of the entropy will be a little different.The Planck unit=c=G=1 has been taken throughout this paper.
2 The Modification Method
For a Schwarzschild black hole,the line element reads

where M is the mass of the black hole.Put it into Klein-Gordon equation for scalar field
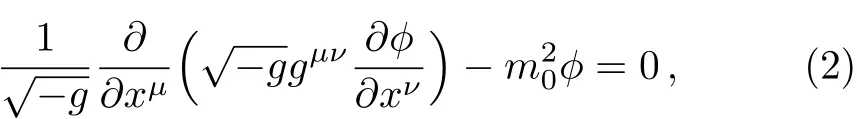
where g= −r4sin2θ is the determinant of the metric.Then one can get

Decompose the wave function into the form of
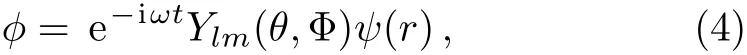
and substitute into Eq.(3),then one could get
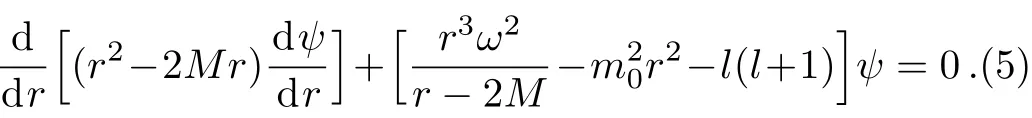
Use Wentzel-Kramers-Brillouin(WKB)approximation,let

put it into Eq.(5),and define a radial wave number k(r,l,ω)by

After takeing the semi-classical quantization condition,the number of radial modes n in membrane model is

where ϵ is the distance between event horizon and the inner membrane surface,δ is the thickness of the membrane.
The cut-o ffis related with parameters ϵ and δ in membrane model,which is chosen by hand,and the physical meaning of the choice is also not very clear.Besides,when ϵ→0,the semi-classical condition might be invalid near the Planck scale.We would like to discuss and reconsider the parameter ϵ.
It is generally believed that the Planck scale exists in our universe[1,17−19]and several theories based on this got some good results.Moreover,the loop quantum gravity theory found the evidence that the space is Planck scale discrete[20]in nature.It announced that the area and volume have discrete spectrum.[21−22]
Besides,many efforts have been devoted to the GUP recently.The simplest formulation of generalize the uncertainty relation reads[23]
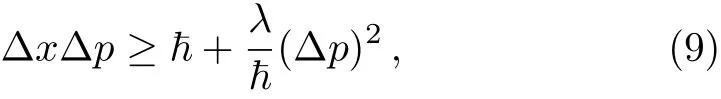

In Ref.[25],the authors also gave the proper distance vicinity near the horizon of order of the minimal lengthBased on those pictures,they use the traditional way to recalculate the entropy of black holes by concerned of the GUP.In Ref.[25],we have

then one can get

where ϵ is the distance between the horizon and the corresponding inner surface of the “membrane” in membrane model.
In Refs.[24–27],the authors calculated the entropy and gave the result in Eq.(11).This might bring us a way to modified the inner distance into a fixed value,which means that we do not need to assume ϵ to be a free number,which might be zero.The physical meaning of Eq.(11)is just the upper bound of the vicinity near the horizon.[24−25]Now that the upper bound has been set,and the membrane is outside the horizon,we now set ϵ into 2λκ.Then we can see that the inner distance ϵ is corresponding to the surface gravity κ of the black hole now.Thus,the value of ϵ stands for a indigenous property of a black hole,which is connected with the black hole.
If we set ϵ=2λκ,Eq.(8)could be rewritten as

Since the scaler field is regarded as pure energy,i.e.as photons,the chemical potential of the photons in thermal equilibrium should be zero.Then the free energy is
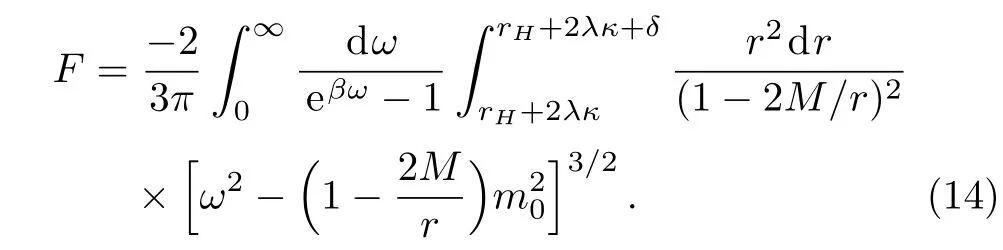
The m0in the latter integral in Eq.(14)will be vanished when r→2M.Then one could get the free energy as

The entropy is

If the cut-o ffis taken as

then,the entropy becomes

One could get δ from Eq.(17)as

Since κ =1/4M,β =1/T=8πM,where T is the temperature of the black hole.Equation(19)could be written as

By using this method,we also get the Bekenstein-Hawking entropy of a black hole.From Eq.(20),we can see that δ is just related to the mass of the black hole itself.The bigger the mass,the thinner the membrane.Since the mass of the black hole could not be in finite,the value of δ could not be zero physically.Then,the standing-wave conditions(13)would always be valid.
In order to see whether the parameter δ is really small enough to form a membrane or not,we could discuss the relationship qualitatively by roughly setting λ=lp=10−35.Then Eq.(20)becomes into

and we could get the plot of δ–M in Fig.1.We could see that the value of δ is very small,which means the membrane is very thin.This decreasing curve implies that the larger the mass,the thinner the membrane.Since the mass of the black hole could not be in finite,the parameter δ would always be positive.The GUP we chose make the semi-classical quantization condition in Eq.(13)always be valid.
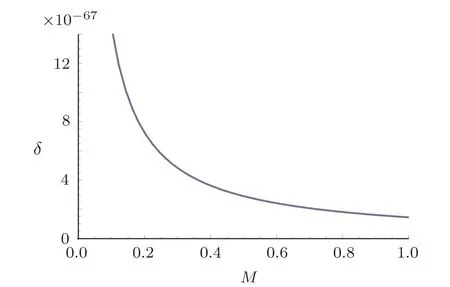
Fig.1 Plot of δ with M of Schwarzschild black hole.
It seems there is nothing special for this modification,the semi-classical quantization may not be quite important.However,when use this modified method to calculate the entropies of Schwarzschild-de Sitter black hole,we find something interesting.
3 The Self-Consistent
For a four-dimensional Schwarzschild-de Sitter black hole,the line element is[29]
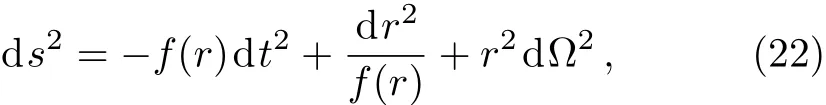
with

where M is the mass of the black hole,Λ is the cosmological constant.The three horizons are[30]
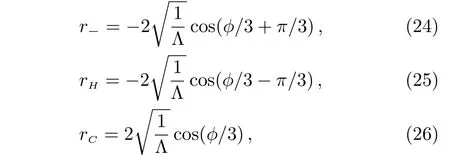
The surface gravity of rHis[30]
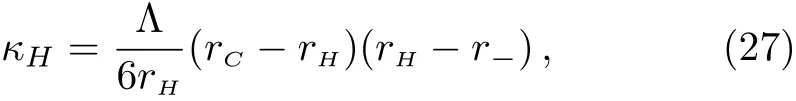
and the corresponding temperature of rHis[30]
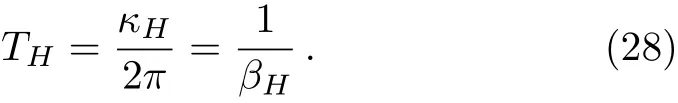
By using the similar calculations with the Schwarzschild black hole in Sec.2,one could gets
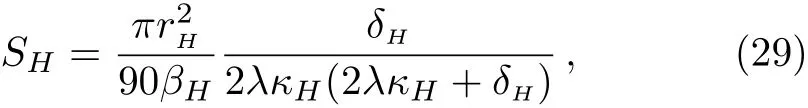
where δHis the thickness of the membrane.If the cut-o ff is as

one could get

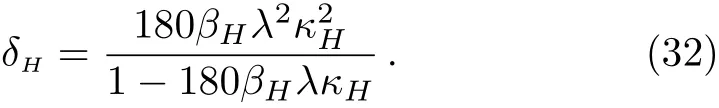
Substituting Eqs.(27)and(28)into Eq.(32)and also discussing the relationship qualitatively by roughly setting λ =lp=10−35and Λ =1,one could get the plot of δ-M in Fig.2.
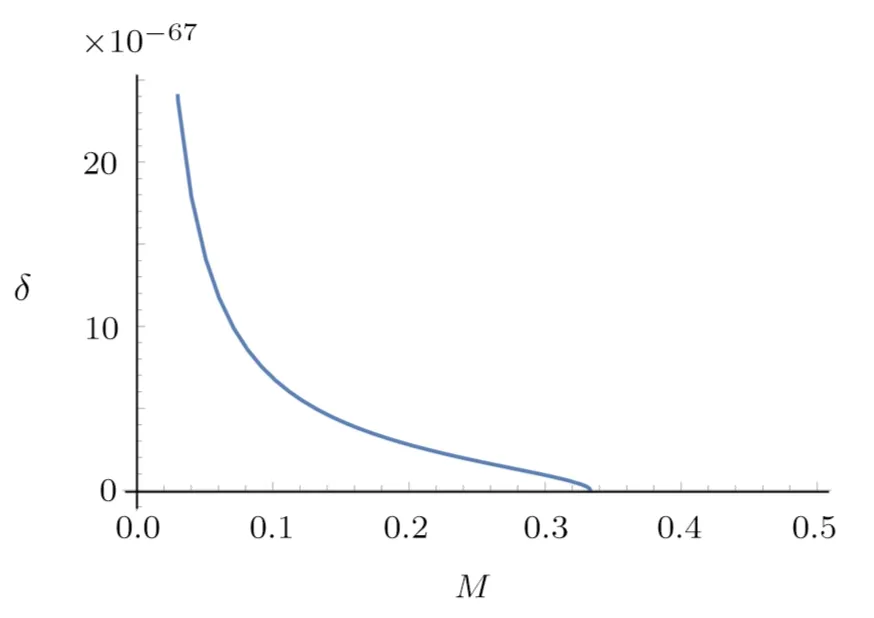
Fig.2 Plot of δHwith 0 From Fig.2 we can see that the thickness of the membrane δHis also inversely proportional to the mass M.But we also see that δHcould be zero in Fig.2.Does this mean that the requirement of δH>0 is wrong? Fig.3 Plot of δHwith 0 To check this,we solve δH=0 from Eq.(32)with Λ =1,λ=lp,then we get M=1/3.For a Schwarzschildde Sitter black hole,it is required that rC>rH.From Eq.(23),we require thatIf Λ =1,then we have 0 Then,by choosing the proper range of M,we could get Fig.3,which is similar with Fig.1.The order of the magnitudes in Fig.3 is also close to the order of the magnitudes in Fig.1.Both of the results show that the parameter δ is very small and just related to the mass M. For a Schwarzschild-de Sitter black hole,we could also get the entropy by natural cut-o ff,which is determined by its mass.Moreover,one could see that the GUP we used might be self-consistent by calculating the entropy of a Schwarzschild-de Sitter black hole,which might reflect the natural of the Planck scale. In summary,by using the results and ideas from the generalized uncertainty principle,we have modified the inner bound of the membrane model and got the Bekenstein-Hawking entropies with cut-o ff s,which were chose by nature rather than by hand.We have also uncovered a result that the thickness of the membrane is only connected with the mass of the black hole itself.The inner distance ϵ is a fixed value,which is determined by the black hole itself with κ as well.Besides,the semi-classical quantization condition could be always valid since the parameter δ is always positive.Since the inner bound is set to a fixed value,we find the requirement of δ also re flects the natural requirement of a Schwarzschild-de Sitter black hole,which means that the GUP we choose is self-consistent and this modification might re flect the physical meaning of the Plank scale.We would like to check this result in other kind of black holes in the future works.
4 Summary
 Communications in Theoretical Physics2018年9期
Communications in Theoretical Physics2018年9期
