Symmetric Surface Momentum and Centripetal Force for a Particle on a Curved Surface

M.S.Shikakhwa

Physics Group,Middle East Technical University Northern Cyprus Campus,Kalkanli,Güzelyurt,via Mersin 10,Turkey

AbstractThe Hermitian surface momentum operator for a particle confined to a 2D curved surface spanned by orthogonal coordinates and embedded in 3D space is expressed as a symmetric expression in derivatives with respect to the surface coordinates and so is manifestly along the surface.This is an alternative form to the one reported in the literature and usually named geometric momentum,which has a term proportional to the mean curvature along the direction normal to the surface,and so “apparently” not along the surface.The symmetric form of the momentum is the sum of two symmetric Hermitian operators along the two orthogonal directions defined by the surface coordinates.The centripetal force operator for a particle on the surface of a cylinder and a sphere is calculated by taking the time derivative of the momentum and is seen to be a symmetrization of the well-known classical expressions.

Key words:quantum mechanics on a curved surface,geometric momentum,quantum centripetal force

1 Introduction

There has been an increase in the interest of the research community in the quantum mechanics of a particle confined to a curved surface.The main reason is evidently the advance in technology that made it possible to fabricate nano-scale curved geometries nano-spheres,nanotubes,etc.A traditional approach to this problem is the Dirac quantization scheme of systems with constraints[1]where the surface equation f(r)=0 is a constraint limiting the number of degrees of freedom available to the system.The standard algorithm of generating secondary constrains and classifying them is applied till one constructs the Dirac brackets of the classical theory,which are then taken over to the quantum theory as the canonical commutation relations.The approach requires the use of cartesian coordinates and su ff ers from the subtlety of operator ordering.[2−4]A more recent approach for the problem is the so called thin layer quantization.[5−6]The idea is to embed the 2D surface into the larger full 3D Euclidean space and achieve confinement of the particle to the surface by introducing a squeezing potential.More speci fically,one considers a curvilinear coordinate system with coordinates u1and u2at the surface,and the coordinate u3in its vicinity in the direction normal to it.The position vector is thus written as R(u1,u2,u3)=rS(u1,u2)+u3û3,whereû3is a unit vector normal to the surface.The Schrödinger equation for a spin zero particle is written in terms of these variables,and the limit q3→0 for a sufficiently strong squeezing potential V(q3)is taken.The Hamiltonian then reduces to the sum of two independent on-surface and transverse parts,with the latter containing only the transverse,i.e.the 3-dynamics.This transverse Hamiltonian is then dropped on the ground that the transverse excitations for a sufficiently strong confining potential have a much higher energy than those at the surface,and so can be safely neglected in comparison to the range of energies considered.This way,one achieves decoupling of the transverse dynamics and is left with only the surface Hamiltonian.For an otherwise free particle,this mechanism generates a geometric kinetic energy term in addition to the standard kinetic energy operator.It worths mentioning here that only very recently[7]it was demonstrated that the geometric potential appears also within a generalized Dirac quantization scheme.Recently,we have introduced[8−10]a new and physics-based approach for confining a particle to a surface that builds on the spirit of the thin-layer quantization but more easier to apply.Another variation of the standard thin-layer quantization was considered in Ref.[11].There,rather than taking the thickness of the layer to zero as in the standard approach,terms of first order in the thickness of the layer were re-entered into the Schrödinger equation on the surface giving rise to corrections to the kinetic energy and the geometric momentum.In recent years the thin layer quantization was applied to a particle in an electromagnetic field,[12−16]a spin one-half particle,especially a one subject to spin-orbit interaction,which became a focus of interest by the condensed matter research community.[17−23]The same squeezing approach of the thin layer quantization procedure was also recently applied to confine a spin-less particle to a curve.[24]

An important question in connection with the quan-tum dynamics on a curved surface is the correct form of the momentum operator on the surface.The expression

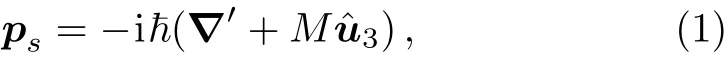
where∇′is the gradient operator on the surface,û3the unit vector normal to the surface and M the mean curvature of the surface was derived in Ref.[25]within the Dirac quantization scheme.The same expression was derived by us within the framework of the thin-layer quantization.[26]This momentum,despite being the momentum operator on the surface has an “apparent” component normal to the surface.However,as was noted in Ref.[26]it has zero projection along this normal direction.In the present work we show how to trade o ffthecomponent of this momentum for an expression(Eq.(14)below)that is symmetrized in the derivatives with respect to the surface variables and manifestly along the surface.

Another question that was more recently addressed is the expression for the centripetal force operator for a particle confined to a curved surface but is otherwise free.It was suggested in Ref.[27]that for surfaces with constant curvature,the expression for the quantum centripetal force is the same as the classical upon applying a simple symmetrizing in order to take care of operator ordering issues.In a more recent work,[26]we have obtained an expression for the centripetal force of a particle on a cylindrical and spherical surface that although“apparently”not radial,was checked to have zero projection along the surface and a radial component formally similar to the classical expression.Here,we derive,starting from the symmetrized momentum and applying the Heisenberg equations of motion an expression for the centripetal force for a particle on the surface of a cylinder and a sphere that is just a symmetrization of the classical expression of this force,namely,with vsbeing the speed on the surface.We check the general form(and show it needs to be slightly modified)suggested in Ref.[27].We also show that the apparently not radial form for this force that we have derived in Ref.[28]can be easily reduced to the symmetric form.In Sec.2 we derive an expression for the mean curvature on a surface spanned by orthogonal curvilinear coordinates(OCC)that will enable us to express the Hermitian surface momentum,Eq.(1),that we derive in Sec.3 in a symmetrized form free of the normal component.In Sec.4 we derive the symmetrized expressions for the centripetal force for a particle on the surface of a cylinder and a sphere.We summarize our results in Sec.5.

2 Mean Curvature for Orthogonal Surface Coordinates

We consider a particle confined to a surface embedded in the 3D space spanned by a set of orthogonal curvilinear coordinates(OCC){ui},i=1,...,3 with the corresponding orthonormal unit vectors.We choose the surface so that the position vector of the particle R(u1,u2,u3)is given as[6]

with r(u1,u2)lying on the surface andis the unit vector normal to the surface and u3is the coordinate along that normal.As was discussed in the introduction,the onsurface condition is achieved by letting u3→0,in which case we have

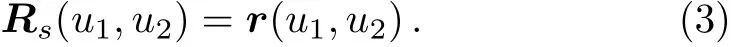
The metric tensor in the curvilinear 3D space has the standard form Gij= ∂iR ·∂jR and that on the surface gab= ∂ar·∂br where a,b run over the surface coordinates 1,2.The two metric tensors are related as[6]

with Ga3=G3a=0,G33=1.T denotes transposing and α is the Weingarten matrix[6]with the elements:

where hab=and g=det(gab).Evidently Gabreduces to gabin the limit u3→0.The mean curvature,M,an extrinsic geometrical quantity is M=(1/2)Tr(α)and the Gaussian curvature is K=det(α).In an OCC system,the form factors hi,(i=1,...,3)are defined through[29]∂iR=whereare the orthogonal unit vectors of the OCC system.In this case,we have g12=g21=0 and g11==.h3=1 evidently since u3has the dimensions of length.Therefore,the expression for the mean curvature for OCC reduces to:

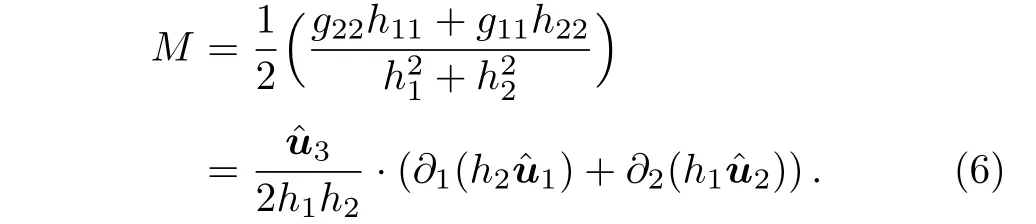
We now invoke the identity

which follows immediately from the requirement that the 3D momentum operator p=be self-adjoint even when the Laplacian is expressed in OCC and keeping in mind that=0.Explicitly:

where integration is over all space with the measure h1h2h3du1du2du3.Hermicity of p demands the vanishing of the bracket on the right hand side,thus the identity(7).Multiplying both sides of Eq.(7)byon the left we get:

which provides an alternative and equivalent expression for M(that was also derived in Refs.[8–9]).At the same time,it implies:

This last identity will have interesting consequences as far as the form of the Hermitian surface momentum is concerned as we will show in the next section.

3 The Symmetric Form of the Hermitian Surface Momentum

The Hamiltonian for a particle on a curved surface constructed using the thin-layer quantization scheme assumes the well-known form:[6,8]

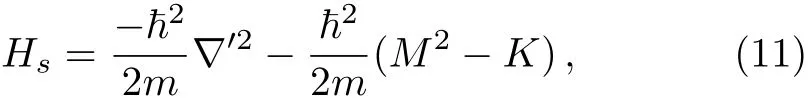
where,

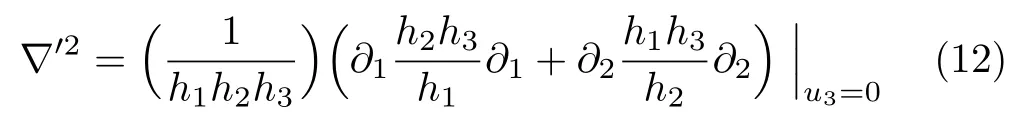
is the Laplacian operator on the surface,M and K are respectively,the mean and Gaussian curvatures defined earlier.The kinematical momentum operator on the surface ps=mvscan be found by calculating the time derivative of the position operator at the surface Rs=r(u1,u2)using the Heisenberg equations of motion:

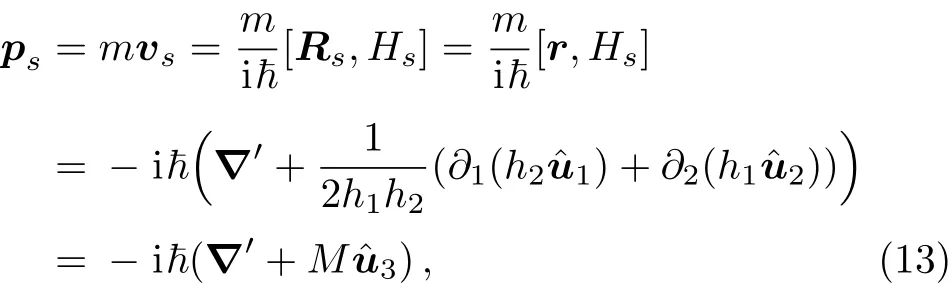
where we have used∂ar=with ha=ha|u3=0in the derivation,which follow from Eqs.(2)and(3).The expression ps=is just Eq.(1)that is also known in the literature as the geometric momentum.[30]Here,however,it follows from the time derivative of the position vector operator at the surface.We can go further and obtain an alternative new expression for ps.The expression given by Eq.(10)forallows us to write:

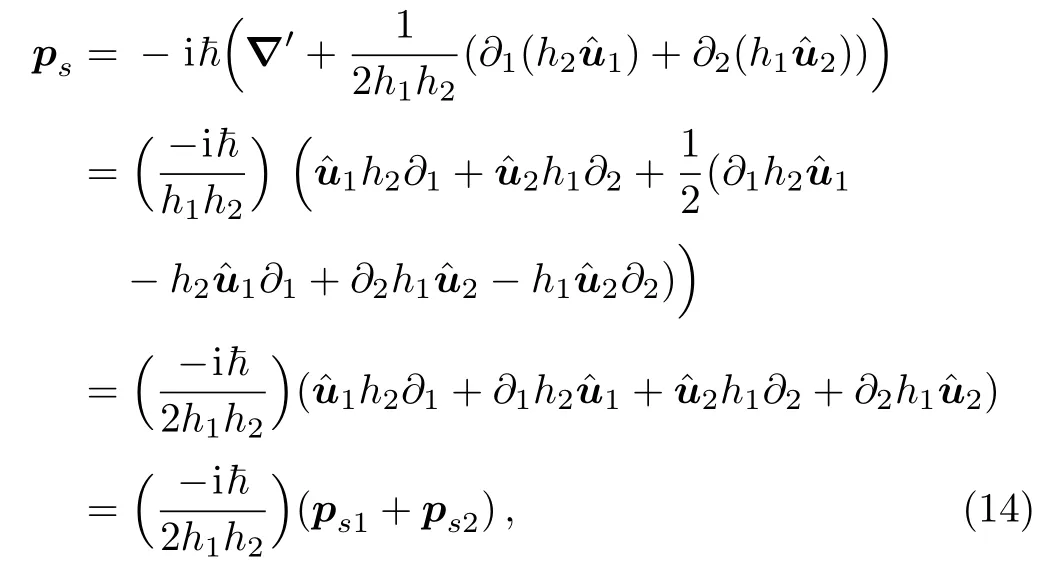
where we have defined the symmetric Hermitian momenta ps1and ps2:

and same for ps2.Note that in the absence of brackets it is to be understood that the differential operators are acting on anything to their right.The above new form of psis remarkable.On the one hand,it makes explicit that it is along the surface with zero projection along.This is in contrast to the form ps=,which has an“apparent” radial projection,which is not the case,however in Ref.[26].Moreover,the fact that one can trade o ffthe presence of the mean curvature in this kinematical surface momentum for a specific symmetric expression of the derivatives suggests that the appearance of the curvature in the momentum is actually a way of dictating this specific symmetric expression upon confining to the surface.In other words,the symmetrization here is not done“by hand” but follows naturally from the mean curvature.Also,each of the momenta ps1and ps2is self-adjoint by itself.This can be checked easily by noting,for instance,that

Here,the integral is over the surface with the measure h1h2du1du2.One can easily check the following orthonormality relations:

So,ps1is the self-adjoint kinematical surface momentum alongand ps2is that along.The symmetrization of operators assumes importance within the framework of the Dirac quantization scheme where operator ordering issues arise as one switches from the classical Dirac brackets to the corresponding quantum commutators.This is because,in general,there is no unique ordering of operators as one switches to the quantum regime.Here,the mean curvature dictates a specific ordering.Of course,the context here is different from the Dirac quantization scheme,and one should keep in mind that the momenta here are the kinematical ones,which need not always correspond to the canonical momenta.The surface Hamiltonian,Eq.(11),can be expressed in terms of psas was shown in Ref.[28]:

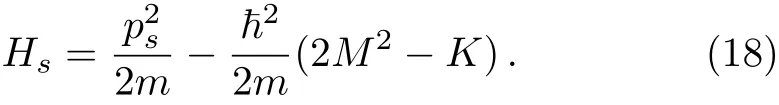
Note that in the second(geometric)term of this last expression we have twice the M2that appears in the cor-responding term of the expression(11)for the Hamiltonian.However,unlike the case in the classical Hamiltonian

4 Symmetric Centripetal Force Operator for a Particle on a Sphere and a Cylinder

Recently,[28]we have used the Heisenberg equations of motionto calculate the centripetal force operator for a particle confined to the surface of a cylinder and a sphere and otherwise free.Although we have found an expression that was not manifestly radial,we have shown that it is indeed radial by demonstrating that it was torque-less and that it has zero projection along the surface.The starting point in the calculation was the surface momentum operators on the relevant surface expressed in the formMotivated by the symmetric expression for the momentum found in this work,we have recalculated this force starting from the symmetric expression of the momentum on the surface of a cylinder trying to keep this symmetry at each stage of the calculation.The resulting expression was just the symmetrized classical expression plus a radial term proportional to the mean curvature:

where(see below)

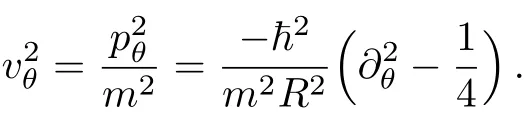
The details of the calculations are as follows. Equations(11)and(14)applied to cylindrical coordinates give,respectively,for the surface momentum and the Hamiltonian:

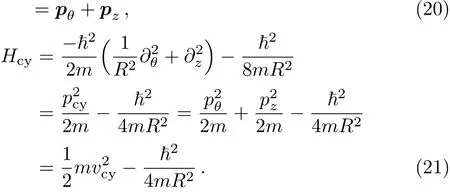
The force operator is found using the Heisenberg equation of motion:

where

The force operator follows by applying the Heisenberg equations of motion giving the result:

The term in the brackets is a symmetrization of the wellknown classical expression for the force.We now make connections with the results reported in Ref.[28].There,the centripetal force for the sphere,for instance,was found to read:

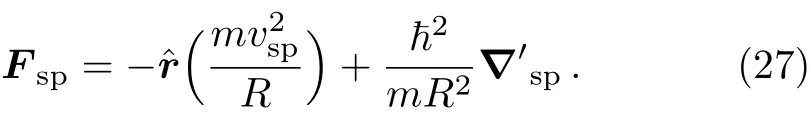
It was shown in that reference that despite the appearance of the second apparently non-radial term the force was radial and torque-less.The above expression reduces immediately to the symmetric force expression given in Eq.(26)just by noting that:

Using this in Eq.(27)gives the symmetric expression for the force,Eq.(26).The same applies for the case of a cylindrical surface.Closing,we note that in the work,[26]an expression(Eq.(20)in the reference)for the quantum centripetal force valid for surfaces with constant curvatures(like the cylinder and sphere)was suggested by making analogy with the classical expression and symmetrizing.It reads:

where κ is the first curvature of the classical orbit,H the free Hamiltonian on the surface andis the normal to the surface.Noting that κ = −1/R for both a sphere and a cylinder and substituting the forms of the free Hamiltonians given in the second lines of Eqs.(21)and(24)on the surface of a cylinder and a sphere,respectively,in Eq.(29)we get the same expression for the force given by Eq.(22)for the sphere.As for the cylinder,there is a discrepancy in that the velocity that appears in Hcyis the full velocityon the cylindrical surface,i.e.it includes the z-component of the velocity,whereas the one that appears in Eq.(26)is the velocity on the classical orbit,i.e.on a circle;.The statement in the above mentioned reference,therefore,needs to be modified,it seems.

5 Summary and Conclusions

We have shown that the Hermitian surface momentum(also known as the geometric momentum[30])ps=mvs=,which is found by taking the time derivative of the position vector operator at the surface can be expressed in the symmetric form,Eq.(14).In this form,psis manifestly along the surface,in contrast to the form in the above line,which “apparently” has a component along,although its projection along this normal direction is zero.[26]Therefore,it is as if the appearance of theis a suggestion of symmetrizing this expression in a specific way.We have also decomposed this momentum into two separately Hermitian operators ps1and ps2,Eq.(16),along the directionsand,respectively.We have also derived the centripetal force operator for a particle on the surface of a cylinder and a sphere and shown that it is a symmetrization of the classical expression for this force.We have compared our results for this force with our previous expressions reported in Ref.[28],and have shown that the latter can be brought to the symmetric more transparent and intuitive forms reported in this work.Our results for the centripetal force can also be viewed as a test of the general expression for the quantum centripetal force expression valid for a surface with a constant curvature suggested by Eq.(20)in Ref.[26],where our results for the cylinder showed discrepancy with this expression and we suggest that it needs modification.