Dirac Equation with a New Tensor Interaction under Spin and Pseudospin Symmetries
C.A.Onate,M.C.Onyeaju,A.N.Ikot,O.Ebomwonyi,and J.O.A.Idiodi
1Physics Programme,Department of Physical Sciences,Landmark University,PMB 1001,Omu-Aran,Nigeria
2Theoretical Physics Group,Physics Department,University of Port Harcourt,Nigeria
3Department of Physics,University of Benin,Benin City,Nigeria
AbstractThe approximate analytical solutions of the Dirac equation under spin and pseudospin symmetries are examined using a suitable approximation scheme in the framework of parametric Nikiforov-Uvarov method.Because a tensor interaction in the Dirac equation removes the energy degeneracy in the spin and pseudospin doublets that leads to atomic stability,we study the Dirac equation with a Hellmann-like tensor potential newly proposed in this study.The newly proposed tensor potential removes the degeneracy from both the spin symmetry and pseudospin symmetry completely.The proposed tensor potential seems better than the Coulomb and Yukawa-like tensor potentials.
Key words:wave equation,eigensolutions,Dirac equation,Nikiforov-Uvarov method,tensor interaction
1 Introduction
The study of Dirac equation with spin and pseudospin symmetries have been a line of great interest in the recent years.[1−15]Dirac equation as a relativistic wave equation,has been used to explain the behaviour of particles in the atomic domain.The symmetry limits(spin and pseudospin)of the Dirac equation introduced in nuclear theory[16−18]are used to explain the real characteristics of deformed nuclei,[19]superdeformation[20]and established effective shell model coupling scheme.[21]Owning to these importance,Dirac equation has been given serious attention using different methodologies such as Nikiforov-Uvarov method,[22−25]supersymmetry quantum mechanics,[26−28]asymptotic iteration method,[29−32]and others.However,one of the fundamental challenging problems facing the study of spin and speudospin symmetries of the Dirac equation is the production of the energy degenerate states which brings about instability of atoms.To solve this problem,a tensor interaction was introduced.The most popularly used tensor term is the Coulomb-like potential.It became clear that the energy degeneracies reduced due to the inclusion of the Coulomb-like tensor term in the Dirac equation.Recently,Hassanabadi et al.,[33]reported the use of Yukawa-like tensor potential as the tensor term.The Yukawa-like tensor potential also removed some energy degeneracy doublets in the spin and pseudospin symmetries.Motivated by this,we propose a new tensor potential as Hellmann-like tensor interaction and investigate the spin and pseudospin symmetries of the Dirac equation with the newly proposed tensor term.This is to ensure a more removal or complete removal of the energy degenerate states in both the spin and pseudospin symmetries.
2 Parametric Nikiforov-Uvarov Method
To use this powerful and elegant method,Tezcan and Sever[34]derived the following from the conventional Nikiforov-Uvarov method

The parameters c1,c2,and c3are the basic parametric constants in which ξ1, ξ2,and ξ3depend upon.From Eq.(1),they obtain the bound-state energy condition as

and the corresponding wave function as

the parametric constants in Eqs.(1),(2),and(3)are defined as[29]follows:

2.1 Dirac Equation in the Presence of Tensor Term
The Dirac equation with both vector potential V(r),scalar potential S(r)and tensor potential U(r)has the form:[35−36]
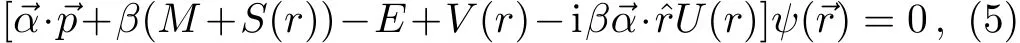
where E is the relativistic energy of the system,M is the mass of the particle p= −i∇ is the three dimensional momentum operator.The total angular momentum Jand the spin coupling k=(·L.+1),where L.is the orbital angular momentum of the spherical nucleus commute with the Dirac Hamiltonian.The eigenvalues of the spin-orbit coupling operator are k=(j+1/2)>0 and k= −(j+1/2)<0 for aligned spin j= ℓ+1/2 and unaligned j=ℓ−1/2.The set(H,K,J2,Jz)forms a complete set of conserved quantities.Hence,the spinors are given as[35−37]


Eliminate Gnk(r)and Fnk(r)from Eqs.(7)and(8)respectively,we have[30−31]

2.2 Spin Symmetry Limit
The spin symmetry limit occurs when d∆(r)/dr=0 and∑(r)=V(r).Hence,Eq.(9)becomes

where we have defined the following for mathematical simplicity:

2.3 Pseudospin Symmetry Limit
The pseudospin symmetry limit occurs when d∑(r)/dr=0 and∆(r)=V(r).Thus,Eq.(10)turns to

where λ1=M − Enk+Cp,λ3=(k+H)(k+H − 1).
3 Approximate Solutions of the Dirac Equation
In this section,we obtain the energy equation and the corresponding wave spinors for the two symmetry limits of the Dirac equation in a close and compact form.It is noted that Eqs.(11)and(15)for spin and pseudospin symmetry limits respectively cannot be solved for k≠0 without the use of approximation scheme.Here,we resort to employ the following approximation scheme:[38−39]

which is valid for δ≪ 1.In this study,the interacting potential called the modified Eckart potential is of the form

3.1 Solutions of the Spin Symmetry
To obtain the solutions of the spin symmetry,we sub-stitute Eqs.(16)and(17)into Eq.(11)and by defining a variable of the form y=e−δr,we have

where


Comparing Eq.(18)with Eq.(1),and by using Eq.(4),we obtain the following

Substituting Eq.(22)for ci(i=1,2,...,9)into Eq.(2),we have energy equation for the spin symmetry as

Substituting Eq.(22)for ci(i=10,...,13)into Eq.(3),we have the upper component of the wave function as

The lower component of the wave function is given as

3.2 Solutions of the Pseudospin Symmetry
To obtain the solutions of the pseudospin symmetry,we substitute Eqs.(16)and(17)into Eq.(15)and by defining a variable of the form y=e−δr,we have

where
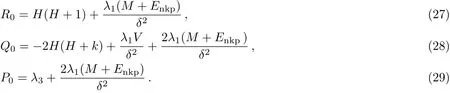
Comparing Eq.(26)with Eq.(1),and by using Eq.(4),we obtain the following

Substituting Eq.(30)for ci(i=1,2,...,9)into Eq.(2),we have energy equation for the pseudospin symmetry as

Substituting Eq.(30)for ci(i=10,...,13)into Eq.(3),we have the upper component of the wave function as

The lower component of the wave function is given as

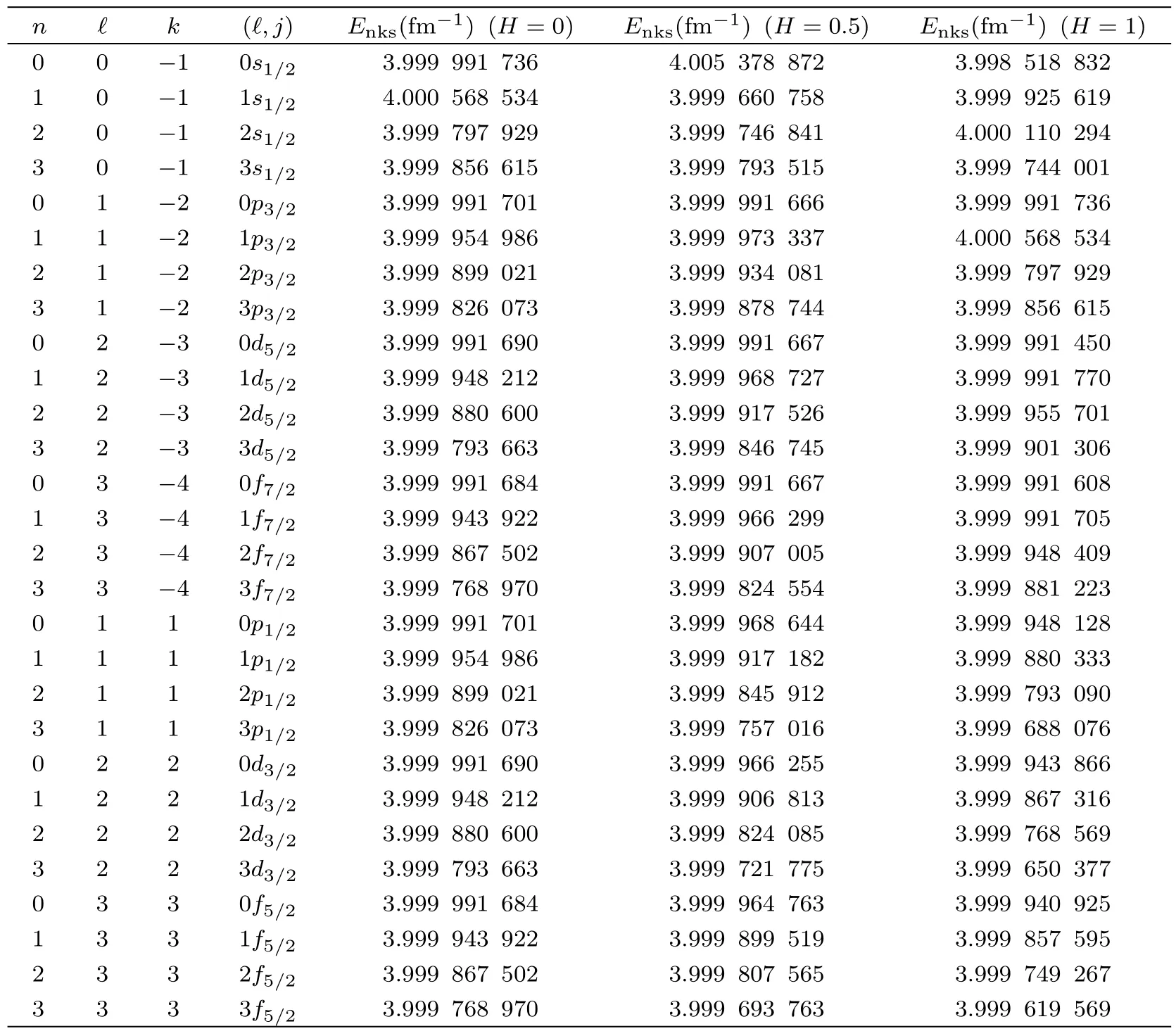
Table 1 Energy in the spin symmetry limit for M=1,Cs=5,δ=0.01,and V=5δ fm−1.
4 Conclusion
The energies for the spin symmetry limit and the pseudospin symmetry limit are presented in Tables 1 and 2 respectively for H=0,H=0.5,and H=1.The energies for H=0 are obtained in the absence of tensor interaction.The usual energy degenerate states 0p3/2=0p1/2,1p3/2=1p1/2,2p3/2=2p1/2,3p3/2=3p1/2,0d5/2=0d3/2,1d5/2=1d3/2,2d5/2=2d3/2,3d5/2=3d3/2,0f5/2=0f7/2,1f5/2=1f7/2,2f5/2=2f7/2,3f5/2=3f7/2are obtained for the spin symmetry limit.For H=0.5,it is observed that the energy degeneracy are removed.Similarly,when H is set to be 1,it is equally observed that the energy degeneracy are completely removed.In the pseudospin symmetry limit,when H=0,which means absence of tensor interaction,we have the following energy degenerate states1s1/2=0d3/2,1p3/2=0f5/2,1d5/2=0g7/2,1f7/2=0h9/2,2s1/2=1d3/2,2p1/2=1f5/2,2d5/2=1g7/2,2f7/2=1h9/2.However,when we set H to 0.5 and 1 respectively i.e.when Hellmann-like tensor interaction is included,the whole energy degenerate states are removed.It seen that of all the tensor potential used such as Coulomb and Yukawa,the Hellmann-like tensor potential is more effective.

Table 2 Energy in the pseudospin symmetry limit for M=1,Cs= −5,δ=0.01,and V=2 fm−1.
 Communications in Theoretical Physics2018年9期
Communications in Theoretical Physics2018年9期
- Communications in Theoretical Physics的其它文章
- Vertical Sediment Concentration Distribution in High-Concentrated Flows:An Analytical Solution Using Homotopy Analysis Method
- Double Wronskian Solutions for a Generalized Nonautonomous Nonlinear Equation in a Nonlinear Inhomogeneous Fiber∗
- Breathers and Rogue Waves Derived from an Extended Multi-dimensional N-Coupled Higher-Order Nonlinear Schrödinger Equation in Optical Communication Systems∗
- Symmetric Surface Momentum and Centripetal Force for a Particle on a Curved Surface
- Effectiveness of Non-Markovian Methods for Quantum Discord Dynamics of Non-coupled Two-Qubit System∗
- Non-Markovian Master Equation for Distant Resonators Embedded in a One-Dimensional Waveguide∗
