基于调制宽带转换器的重构算法研究

杨文举 邹峰

摘 要：本文针对OMP算法需要已知稀疏度的缺陷，提出了一种全盲的基于调制宽带转换器的SAMP算法，并利用此算法进行仿真分析，然后与OMP算法进行比较，分析这两种算法的性能，得出SAMP算法在未知目标信号的稀疏度的情况下能和OMP算法一样实现目标信号的频谱重构。

关键词：压缩感知理论；调制宽带转换器；重构算法

中图分类号：TN911.7 文献标识码：A 文章编号：1003-5168（2018）19-0054-04

Research on the Signal Reconstruction Algorithm Based on the

Modulated Wideband Converter

YANG Wenju ZOU Feng

（The 723 Institute of CSIC，Yangzhou Jiangsu 225001）

Abstract： In this paper， a totally blind SAMP algorithm based on modulation wideband converter was proposed in this paper， which required the known sparsity of the OMP algorithm. This algorithm was simulated and analyzed by this algorithm. Then compared with the OMP algorithm， the performance of the two algorithms was analyzed. It was concluded that the SAMP algorithm could be calculated with OMP in the case of the sparsity of the unknown target signal. The same method was used to realize the spectral reconstruction of the target signal.

Keywords：compressed sensing theory；modulated wideband converter；reconstruction algorith

1 调制带宽转换器

调制带宽转换器作为一种全盲的和实用的欠奈奎斯特采样系统，与传统的奈奎斯特采样系统有很大区别，其在模拟信号转换成数字信号的过程中，直接把传统采样中的采样和压缩过程合二为一，采样之后的数据是已经压缩好的失真数据[1]。调制宽带采样系统是一种随机解调采样系统的多路并用，在利用远低于奈奎斯特采样率的情况下，较好地实现了对多频带未知稀疏性信号的采样，但带来了另一个难题，就是如何把采样之后的信号进行无失真的、理想的重构出原始目标信号的频率谱。调制宽带转换器的原理见图1。

调制宽带转换器虽然在理论上有很大优势，使人们能很好地对多频带未知稀疏信号进行采样，但其还存在很多亟待解决的问题。首先，重构算法的性能不高，现有的重构算法在成功率、可重构的最大频带数和所需的通道数量等方面性能不太好，在现实环境中达到理论性能的极限值还有较大差距。此外，在有噪声的情况下，重构算法性能更差，需要进行大量研究。其次，在采样过程和重构过程中会有严苛的条件要求，在现实环境中，很多信号各个频带的数量和最大带宽都是无法预知的，因此，在实际应用中，必须采用全盲的采样方法，这进一步提高了对重构算法的性能要求。

2 频率谱重构的充分条件

调制宽带转换器系统对于信号是未知的，很多频带在信道中有很多可能的情况，有可能各个频带在信道中是相邻的，也有可能是不相邻的，很难得到目标信号的最大频率。此外，在特定的时间内占用的頻带数量也不知道。面对这么多未知状况，必须对多频带稀疏性信号的信号模型进行重新定义，这样才能在不知道最大子频带带宽及子频带数量的情况下进行信号重构[2]。

调制宽带转换器的采样原理就是通过混频器进行调制，然后通过低通滤波器进行滤波，得到一个输入信号和采样信号的关系表达式：

[aiej2πfTs=n=-R0R0pinXf-nfp，f∈Fs=-fs/2，f/2s] （1）

然后，进行数学推导和演算，对这个式子两端同时进行离散时间傅立叶变换的逆运算表达形式为：

[Yn=?Xn] （2）

其中，[Yn=y1n，y2n，…，ymnT，Xn=x1n，x2n，…，xLnT，n∈Z]。根据数学矩阵知识可知，式（1）中，[?]是[m×L]矩阵，[?i（n）=pi（n）]且[m设多频带的信号[xt]包含任意数量的频带，笔者利用调制宽带转换器系统进行采样，如果下列条件成立，则[Xf]就会有唯一解，原始目标信号就能无失真地恢复。

①[fs≥fp]，并且[fs/fp]数值不能很大。

②一个周期内[pit]的符号数[M≥Mmin=2fQ2fp+12-1]。

③[m≥2K]，其中[K=sup pxFs]。

④观测矩阵[?]的任意2K列线性无关。

3 频谱感知中通道个数的确定

对多带稀疏信号是未知的，必须根据实际情况对联合稀疏度进行估算，然后估计出对目标信号进行采样需要多少个通道并行随机解调，即要估计出所需要的通道数m。

在[fs=fp]作为最基本的配置情况下，假设在实际频谱中第i个子频带[Ai]将自己带到向量[Xf]的非零元素的数量记作[IAi]。根据调制宽带转换器采样技术的频域行为，并考虑频带位置的随机性，可以得到如式（3）所示的表达式：

[Ai/fp≤IBi≤Ai/fp+1] （3）

因此，所有的频谱都进入到[Xf]中的非零元素数即联合稀疏度满足关系表达式（4）：

[iAi/fpIXfiAi/fp+1] （4）

调制宽带转换器的通道个数虽然跟稀疏信号的稀疏度有关，但不需要精确地知道稀疏信号的稀疏度，只要使其通道个数不小于目标信号的稀疏度的2倍即可。

4 重构算法的研究及优化

正交匹配追踪算法（OMP）的整体框架如图2所示。正交匹配追踪算法可以分成2大步骤：感知和重建。感知过程就是寻找最佳匹配原子的过程，由最佳匹配原子确定出支撑集；重建过程就是利用已确定支撑集不断去逼近原信号。2个过程不断迭代，直到满足相应的迭代终止条件，最后重构出原始信号。

由于OMP算法需要已知稀疏度，因此，对现实环境中很多稀疏度未知的多频带稀疏信号无法很好地进行信号重构。本文在稀疏度未知的情况下，对该算法进行优化，将迭代终止准则设置为残差值小于预置的门限，进而提出稀疏度自适应匹配追踪算法。

5 稀疏自适应匹配算法

在稀疏自适应匹配追踪（Sparsity Adaptive Matching Pursuit，SAMP）算法中，稀疏度是未知的。SAMP算法充分利用了“自底向上”和“自顶向下”重构思想的优点，可以在未知稀疏度的前提下实现精确重构。探索了当信号的稀疏度未知时，如何继续利用算法重构信号的问题。SAMP算法引入了参数步长[s]，并假设稀疏度[K=s]，然后进行算法迭代。如果满足迭代停止条件，则重构完成；否则，改变稀疏度，使[K=j×s]，进入下一次算法迭代。SAMP算法流程如下。

输入：[M×N]测量矩阵[?]，[M×1]数据向量y，步长s。

输出：支撑集[T=Tk]，估计信号[x∈RN]，[x1，…，N-T=0]，且[xT=?Ty]。

初始化：[x0=0，r=y，k=0]，估计支撑集[T0=?]，估计稀疏度[K=S]，k是迭代次数，阶层[j=0]，索引集[Λ0]为空集。

①初始选择[Sk={向量?*rk-1中前K]个量级最大元素的索引}；

②[k←k+1]；

③找出残余分量[r]与采样矩阵中最匹配原子的索引[λk]，即[λk←argmaxrk，?j]；

④更新索引集[Λk=Λk-1?λk]，并相应更新采样矩阵中的列集合[Λk=Λk-1?λk]；

⑤重建目标信号，[x←?Ty]，其中[?T]表示矩阵的逆；

⑥更新残余分量[r←y-?kx]；

⑦如果[rk2rk-12]，则[j=j+1，K=j×s]；否则[k=k+1]进行循环迭代直到[rk2ε]，停止迭代。

从SAMP算法流程可知，当步长s较小时，计算复杂度较高，重构性能也较高；当步长s较大时，计算复杂度较低，重构性能会有所降低。对于任意稀疏度为K的信号X，如果测量矩阵[?]满足带有参数[δ3k<0.06]的3Ks阶RIP条件，则在有限次迭代后，稀疏自适应匹配追踪算法能够从[y=?x]中正确地重构出目标信号的频谱，其中[Ks=sK/s]，s表示步长。

6 仿真结果及分析

在调制宽带转化器采样过程中，仿真采用数字的方法替代模拟信号处理，在采样过程中，首先要用混频器扩展信号的频带，模拟混频器用数字乘法器进行代替，低通滤波器用一个高阶的数字滤波器进行代替，低速ADC可以用数字抽取的方式进行代替，本文采取的仿真过程如图3所示。

为了进行采样之后重构算法的验证，设计了下述5个步骤，然后与OMP算法的性能进行比较。

①目标稀疏信号的产生由表达式（5）形成。

[xt=i=12/NEiBisincBit-τicos2πfit-τi] （5）

②将信号的能量系数Ei设置为1，带宽Bi设置为100MHz，信号的采样率设置为10GHz；按照调制宽带转换器采样理论设置MWC采样参数：通道m设为40，每个通道的采样率[fs=fp=fNYQ/195=51.28MHz]。

③将设置好的信号通过乘法器进行扩频，然后再通过数字滤波器进行滤波，对滤波之后的信号进行数字抽取，抽取值（采样频率）为M。

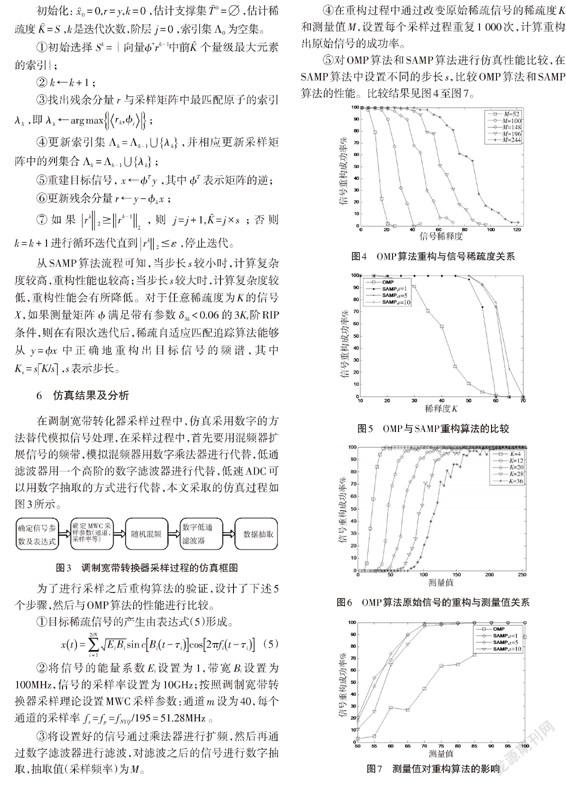
④在重构过程中通过改变原始稀疏信号的稀疏度K和测量值M，设置每个采样过程重复1 000次，计算重构出原始信号的成功率。

⑤对OMP算法和SAMP算法进行仿真性能比较，在SAMP算法中设置不同的步长s，比较OMP算法和SAMP算法的性能。比较结果见图4至图7。

从图4至图7可以看出，当目标信号的稀疏度一定时，无论是OMP重构算法还是SAMP算法，测量值越多，信号重构的成功率就越高。OMP重构算法受目标信号稀疏度的影响较大，而SAMP重构算法受到的影响相对来说较小。对于SAMP算法，步长s越大，对目标信号的迭代就越小，重构性能也变差。从上述研究结果可以看出，SAMP算法可以在不需要知道稀疏度的情况下精确地实现原始信号的重构，且重构率良好，与OMP算法的重构率表现得很相近。

7 基于调制宽带转换器的频谱感知应用实例

受条件限制，没有设计出硬件系统进行实际采样和信号重构，欠采样的前端设计和信号重构都是用仿真实现的。

本文采用4通道示波器对原始信号进行欠采样，然后对采样之后得到的数据用SAMP算法进行重构。在实际环境中对目标信号进行欠采样，然后利用SAMP算法对采样之后的信号进行重构，该应用实例的原理见图8。

首先，设置一个原始稀疏信号[xt]，该信号由2个频带组成，第一个子频带的中心频率为0.1GHz，带宽为0.04GHz；另一个子频带的频率中心为4.8GHz，带宽为0.1GHz，其波形如图9所示，将原始信号在MATLAB中进行混频处理及数字滤波器进行滤波。其次，将产生的信号载入信号发生器，并使其进入示波器通道，设置每个通道的采样率为200MHz，进行采样。最后，将采样之后的数据保存导入MATLAB中进行信号重构，得到重构信号的频谱如图10所示。原始稀疏信号较好地被恢复出来。可见，SAMP重构算法具有良好的重构性能，其在现实环境中也是有效的。

8 结语

本文首先介绍了OMP算法，然后提出一种全盲的基

于调制宽带转换器的SAMP算法，利用此算法进行仿真分析，然后与OMP算法进行比较，分析这两种算法的性能，得出SAMP算法在未知目标信号的稀疏度的情况下能和OMP算法一样实现目标信号的频谱重构。此外，对基于调制宽带转换器的SAMP算法重构利用示波器进行采样，证明SAMP重构算法的有效性。

参考文献：

[1]Zhao Y. Model-Based Multichannel Compressive Sampling with Ultra-Low Sampling Rate[J].Circuits Systems & Signal Processing，2012（4）：1475-1486.

[2]Buckner Z D，Reed M L，Aylor J H. Antialiasing Encoder Interface With Sub-Nyquist Sampling[J].IEEE Transactions on Instrumentation & Measurement，2006（6）：2029-2033.

[3]黃振，柏正尧，莫禹钧.调制宽带转换器与多陪集采样在稀疏多频带信号采样中的应用[J].云南大学学报（自然科学版），2014（4）：477-483.

[4]郑仕链，杨小牛.用于调制宽带转换器压缩频谱感知的重构失败判定方法[J].电子与信息学报，2015（1）：236-240.

[5]黄振，柏正尧，莫禹钧，等.基于调制宽带转换器的倒谱恢复算法[J].南阳理工学院学报，2013（6）：22-24.

[6]宁刚.基于压缩感知的信号重构算法研究[D].长春：吉林大学，2010.

[7]霍迎秋.多维稀疏信号重构算法研究及应用[D].咸阳：西北农林科技大学，2015.

[8]葛进波.基于压缩感知的重构算法与应用研究[D].广州：华南理工大学，2015.