针对ATM市场的特征参数提取研究

谢鹏飞 王文杰 田昊放 陈丽娟

摘 要：近年来，我国ATM保有量持续攀升，ATM市场发展迅猛。为了全面的分析ATM交易状态特征，本文通过提取出特征参数，为设计出准确度高、适应性强的交易状态异常检测方案做了相关铺垫。依据拉依达准则剔除异常数据，并分析SPSS软件对业务量、交易成功率和交易响应时间之间的相关性分析结果，确定了各指标之间的相关性。使用双次N值比较法，以交易成功率的平均值y和方差σ2作为交易成功率特征参数。

关键词：特征参数 ATM市场 双次N值比较

中图分类号：F069 文献标识码：A 文章编号：2096-0298（2018）08（c）-180-02

在互联网金融浪潮下，ATM市场寻找增长动力的同时，也要注重“质”的提升。通过对ATM交易状态的特征分析与异常检测，不仅可以捕捉ATM应用系统的运行情况，提高ATM的服务水平和服务质量，而且可以及时发现和处理交易系统的异常情况，为ATM市场的发展保驾护航、提供动力。

1 异常数据的剔除

首先，使用Matlab软件绘制业务量—交易成功率—交易响应时间散点图，通过图1观察，初步确定数据中存在异常点。为了减小后续计算过程中的误差，因此采用拉依达准则剔除异常数据。

已知业务量的变化存在以下特征：工作日和非工作日的业务量存在差别；一天内，业务量也存在业务低谷时间段和正常业务时间段。因此在剔除异常数据时，不以业务量为主要指标进行剔除操作，而是针对成功率和响应时间这两个指标，采用拉依达准则剔除异常数据。拉依达准则，即3倍标准偏差法。当某一测量数据与其测量结果的算术平均值之差大于3倍标准偏差时，该测量数据应舍弃，用公式表示为：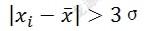

在剔除异常数据前，响应时间的平均值为100.7657，标准差601.4808；成功率的平均值为0.9586，标准差为0.0276。在剔除异常数据后，响应时间的平均值为91.5838，标准差为14.8084；成功率的平均值为0.9605，标准差为0.0199。经过剔除异常数据的操作，响应时间的标准差由601.4808降低至14.8084，成功率的标准差由0.0276降低至0.0199，响应时间、成功率标准差的降低说明波动大的异常变量已被剔除，由此可以确定拉依达准则有效地剔除了异常数据。

在剔除异常数据后，使用Matlab软件绘制业务量—交易成功率—交易响应时间散点图，图2可以直观的发现波动较大的异常变量已被剔除。因此，进一步确定，通过拉依达准则，有效地剔除了异常数据。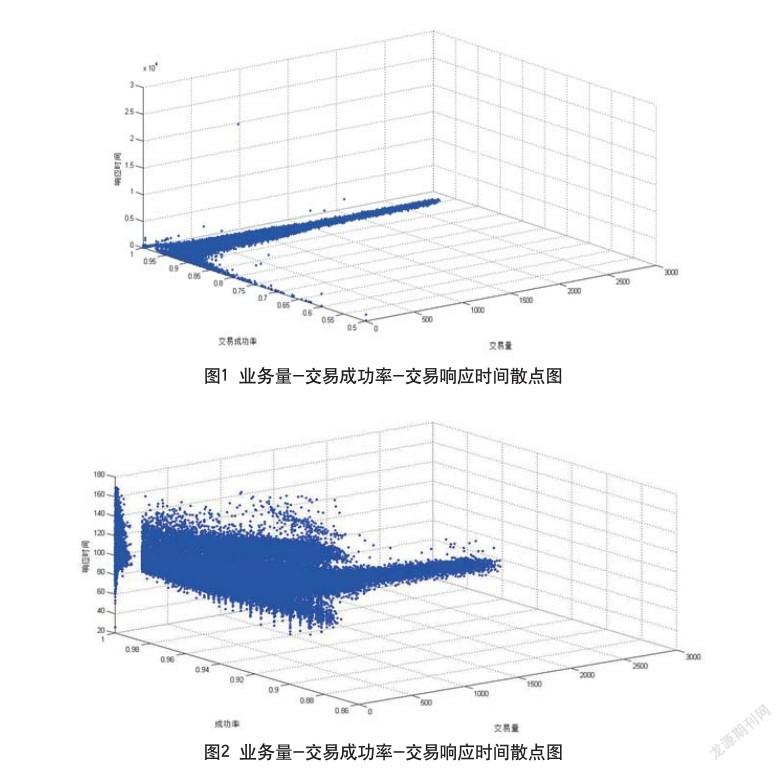

2 相关性分析

为了分析三个指标之间的相关性，本文使用SPSS软件对数据进行了相关性分析，得到业务量—交易成功率—交易响应时间相关性分析结果，如表1所示。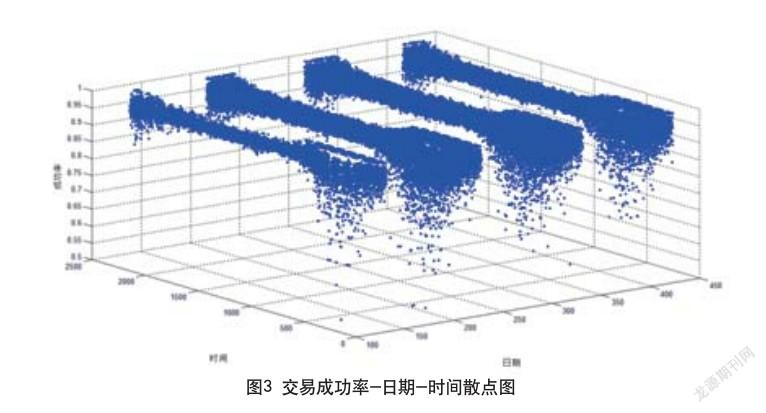

根據业务量—交易成功率—交易响应时间相关性分析结果，成功率与业务量的显著性概率为0.276，大于显著水平，相关性不显著；相关系数为-0.010，则成功率与业务量基本不相关。成功率与响应时间的显著性概率为0.035，小于显著水平，相关性显著；相关系数为-0.019，相关程度弱，则成功率与响应时间基本不相关。业务量与响应时间的显著性概率为0，小于显著水平，相关性显著；相对系数为-0.588，则业务量与响应时间负相关，相关程度为中度相关。

基于相关性的分析，得出如下结论：成功率与业务量基本不相关，成功率与响应时间基本不相关，业务量与响应时间负相关，相关程度为中度相关。

3 提取特征参数

通过分析图3，可 以得出以下结论：在日期相同的条件下，在凌晨和深夜时分散点的离散程度高。成功率主要维持在0.95左右。因此，用方差分析法来寻找其置信区间。

此处应用方差分析法计算交易成功率与其均值的离散程度。当数据变化的绝对值超过N倍标准均方差变化阀值的数据个数达到一定标准时，说明数据存在异常。

通过观察和分析交易成功率—日期—时间散点图，发现成功率存在离散程度很高的数据，因此使用双次N值比较法。根据双次N值比较法的需要，先进行第一次N值比较处理，在去除极端异常值之后，以交易成功率的平均值y和σ2方差作为其特征参数：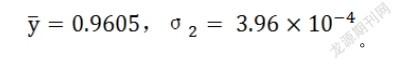

4 结语

本文为了得到更准确的特征参数，首先要进行数据预处理，依据拉依达准则进行异常数据的剔除。为了分析三个指标之间的相关性，使用SPSS软件的相关性分析结果确定了三个指标之间的相关性。采用双次N值比较法，通过第1次N值比较去除干扰后，以交易成功率的平均值y和σ2方差作为其特征参数。

参考文献

[1] 柴洪峰.基于数据挖掘的异常交易检测方法[J].计算机应用与软件，2013，30（1）.

[2] 孙萌.A银行风险控制研究[D].苏州大学，2016.