中药质量源于设计方法和应用：工艺放大

罗赣 徐冰 孙飞 马群 史新元 乔延江

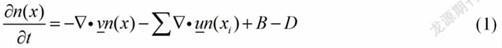
摘要 当制药工艺从实验室小试规模向生产规模放大时，工艺规模成为影响产品质量的新的变量。小试规模下工艺参数对产品质量的影响在中试规模或生产规模下可能呈现另外情况。在质量源于设计（QbD）框架下，加入工艺规模这个新的变量，势必对制药过程的理解提出了更高要求。本文总结了常用制药工艺放大的方法，并重点介绍了数学模拟放大。以高速剪切湿法制粒过程为例，通过采用量纲分析，保持各规模间颗粒增长微环境的动力学和热力学相似，建立非规模依赖型工艺动态设计空间，扩展了设计空间的边界和范围，提高了工艺对变化因素的容忍性，产品可变性得到有效控制。

关键词 质量源于设计;工艺放大;动态设计空间;高速剪切湿法制粒过程;模式地图

Chinese Medicine Quality Derived From Design Methods and Applications for-（Ⅳ）：Process Scale-up

Luo Gan1， Xu Bing1， Sun Fei2， Ma Qun1， Shi Xinyuan1， Qiao Yanjiang1

（1 School of Chinese Medicine， Beijing University of Chinese Medicine， Beijing 100029， China; 2 School of Chinese Medicine，

Guangdong Pharmaceutical University， Guangzhou 510006， China）

Abstract When a pharmaceutical process was transferred from lab to industry， the process scale became a new variable which had impacts on the product quality. Under the framework of pharmaceutical quality by design （QbD）， the addition of process scale as a new variable need further understandings of pharmaceutical processes. This paper summarized common methods for pharmaceutical scale-up study. In particular， mathematical modeling and simulation based scale-up methods were introduced in detail. The high shear wet granulation process was selected as an example. Dimensionless analysis was performed to maintain the similar dynamics and thermodynamics of micro environment of particle growth at different scales. And then process dynamic design space was built and was dimension independent. The boundary and range of process design space were extended. The tolerance of process for changeable variables was improved and quality variability of the product was well controlled.

Key Words Quality by design; Process scale-up; Dynamic design space; High shear wet granulation process; Regime map

中图分类号：R283.3文献标识码：Adoi：10.3969/j.issn.1673-7202.2018.03.002

1 分类综述

1.1 制剂工艺开发的一般步骤 制剂工艺开发的一般步骤：文献查阅-实验室研究（小试工艺）-中试研究-工业化生产。表1从目的、规模等方面列举了小试工艺与工业化生产工艺的不同之处，可见随着生产规模的扩大，工艺过程的总体行为、物理状态、反应条件以及原辅料的质量情况都发生较大程度的变化。而中试研究是连接小试工艺与工业化生产工艺的桥梁，起到承上启下的作用。一般来说，工艺研究先从实验室究放大到中试级别，再放大至生产级别。

表1 小试工艺与工业化生产工艺的比较

表2 放大设计的定量工程方法

1.2 工艺放大的方法

1.2.1 经验放大 主要凭借经验通过逐级放大来摸索反应器的特征，包括试验装置、中间装置、中型装置、大型装置。目前在合成药物的工艺研究中，中试放大主要采用经验放大法，同样也是化工研究中的主要方法。由于中药制药过程流程长，操作单元多，机理机制多数不明确，同样经验放大在中药制药过程中使用较为广泛。由于对过程缺乏足够的理解，开发时间长，耗资大，且所得结果非常不可靠，在放大过程中会出现各种各样的“放大效应”，导致中试、生产的产品质量不合格或其他指标不合格。

1.2.2 相似放大 主要应用相似原理进行放大。相似原理包括设备几何相似，運动学相似，动力学相似。但利用相似原理放大，仅局限于物理过程。对于复杂的制药过程，相似放大的普适性受到极大的限制。

1.2.3 数学模拟放大 数学模拟放大是应用计算机技术，基于模型的放大。今后会成为放大理论研究的主要方向。摆脱经验设备的限制，将过程模型化应用在工艺放大中。而过程模型化正是QbD的核心[1]，故数学模拟放大，基于过程模型研究放大过程，恰是QbD在制药过程放大研究中的应用实例。随着对过程知识和理解的深入，可用来指导放大研究的有3种常用的建模方法。见表2。

在物理科学界的流体动力学和化学工程学领域，长期以来合理的放大方法已经有所应用。这种方法是基于在不同的规模下的过程相似性使用量纲分析来进行放大。量纲分析在一个世纪之前已经在诸如化学工程学等许多工业领域得到了广泛的认可[2]。量纲分析是利用无尺度参数完全表征过程特点的方法。当控制过程的模型未知时，量纲分析依然适用。根据模型理论，2个过程如果具有相似的几何空间并且描述过程的所有无尺度参数具有相同的数值，那么这2个过程可以认为是完全相似的。那么放大研究就可以用一系列的无尺度的参数对过程进行描述，并且在不同规模下对比这些数字。在无尺度参数构建的空间中存在的测量值或测量方法使得工艺规模成为不可变的量，也就是说在不同的工艺规模下，无尺度空间内的测量值同样适用。

作为QbD方法中重要的元素，设计空间在某一固定实验规模下可以提升过程的稳定性，给予操作者灵活的操作空间[3]。而当工艺规模发生变化时，例如从小试到中试，再到大生产，产品的质量属性很难保持一致，而小试规模下的设计空间在中试、大生产上很难适用。若在无尺度空间下构建设计空间，摆脱工艺规模的限制，则可以保持设计空间相对稳定，开发出相应的动态设计空间来指导放大。

1.3 应用实例—高速剪切湿法制粒（High Shear Wet Granulation，HSWG）过程的放大研究

1.3.1 HSWG过程建模的发展

一般来说，高速剪切湿法制粒过程是非常难以设计和放大的。首先，在制粒机内部同时发生许多不同的速率过程，颗粒属性的形成是这些速率过程共同作用的结果，例如颗粒粒径分布、密度及粘合劑分布。这些过程大致可以分为3个阶段：润湿与成核、成长与致密化、磨损与破碎[4]。完美的机理模型需要对这些过程进行合理的解释，并能够通过处方变量和过程变量的变化准确的预测过程可能会发生的变化以及对最终产品质量的影响。其次，湿法制粒中制剂软材的形成机制非常复杂，高速剪切湿法制粒过程尤甚，且受设备几何构造的影响，是非常难以预测的。经过了近50年的发展，湿法制粒过程建模经历了3个阶段：粒算平衡方程、数值计算模拟、无尺度参数建模。详细介绍如下。

1.3.1.1 粒算平衡方程建模 在上世纪60年代到80年代，作为第一代湿法制粒过程建模方法，粒算平衡方程（Population Balance Equation，PBE）在当时引起了广大研究者的兴趣。粒算平衡方程是关于数值密度函数的连续形式，该方程为非线性双曲型方程，且通常求解域为半无穷域，没有一般意义的分析解，数值求解成为研究该方程的主要手段[5]。1971年，Randolph和Larson[6]提出了粒算平衡方程的一般形式：

式中xj表示颗粒的固有参数，n表示颗粒的数量，表示速率，B表示生长项，D代表消失项。

后来，不断有学者对该建模方法进行探索[7-9]。20世纪90年代后，群体平衡方程模型被大多数学者用来预测制粒过程中某些速率常数[10-11]。大多数学者在应用群体平衡方程模型时，过于重视研究颗粒成长和致密化的过程，而忽视了润湿和粘合剂的加入对制粒过程的影响[12-13]，因此限制了该模型的应用。

1.3.1.2 数值计算模拟 该方法基于离散元模拟（Discrete Element Simulations，DEM）、蒙特卡洛仿真（Monte Carlo Simulations，MCS）、计算流体力学（Computational Fluid Dynamic，CFD）等模拟和分析研究颗粒流的问题。离散元的思想源于较早的分子动力学，其主要思想是把整体的递质看作由一系列离散的独立运动的粒子（单元）所组成，单元本身具有一定的几何（形状、大小、排列等）和物理、化学特征，其运动受经典运动方程控制，整个递质的形变和演化由各单元的运动和相互位置来描述[14]。

蒙特卡洛仿真是通过大量的计算机模拟来检验系统的动态特性并归纳出统计结果的一种随机分析方法。运用蒙特卡洛仿真解决问题首先要建立与描述该问题相似的概率模型，然后对模型进行随机模拟或统计抽样，再利用所得到的结果求出特征的统计估计值作为原问题的近似解，并对解的精度做出某些估计。

计算流体力学是采用数值方法利用计算机来求解流体流动的控制偏微分方程组，并通过得到的流场和其他物理场来研究流体流动现象以及相关的物理或化学过程。计算流体力学的控制方程就是质量、动量和能量守恒方程，如式（2）～（4）所示[15]。流动控制方程组的精确解是流场计算域内流动参数的连续分布，数值解则是流场计算域内离散的点上的近似解对连续精确解的逼近，通过把连续的流场离散为一定数目的不连续的点，对于这些离散点，近似满足3个守恒方程，当离散点之间的距离为无穷小，近似解无限趋近于精确解。

方程（2）～（4）中，p表示流体的密度，t表示时间，x是坐标，u是速率，P是流体的压力，H是流体的熵，τ是剪切应力，i、j、k表示三维坐标的方向，Sm表示质量源，Sf表示动量源，Sh是能量源。

目前，数值计算模拟的方法在流化床制粒过程研究中取得显著的进展[16-21]。对于剪切制粒过程，只论证了该方法的可行性。Justin等[22]采用离散元模拟的方法对高速剪切湿法制粒过程粒径分布的动态变化进行了模拟预测，结果表明：在湿法制粒过程中，粘合剂的加入形成粘合剂层，从而引起动力学诱导效应产生颗粒的快速成长，进而导致致密化过程。Terashita等[23]通过讨论不同填充量对颗粒固相率、颗粒速度、颗粒速度矢量、动能以及流动模式的影响，采用离散元模拟的方法确定高速剪切湿法制粒起始材料的最佳填充水平。数值计算模拟的方法对制粒过程的定性理解做出一定的贡献，但对于过程参数的定量预测仍然处于空白，以至于制粒过程的控制仍然以经验为主，并非基于对制粒过程的深刻理解[24]。

1.3.1.3 无尺度参数建模 该方法是针对颗粒形成经历的润湿和成核、成长和致密化、磨损和破碎三类速率过程，建立模式地图（Regime Map）。利用建立起的模式地图预测湿法制粒过程中粘合剂的分布和颗粒变形的行为。目前报道出的研究较为成熟的Regime Map包括润湿与成核Regime Map和成长与致密化Regime Map，详述如下：1）润湿与成核Regime Map：润湿与成核是湿法制粒过程的第1步。粘合剂液滴滴入到移动的粉末床表面形成了颗粒的前体：颗粒核。颗粒核的形成过程随着粘合剂和粉末床的流动速率、粘合剂和粉末床的接触方式、以及液滴完全渗透到粉末床所需要的时间的不同而不同。在该阶段存在2个重要的竞争过程，第1个是液滴喷到粉末床的速率与粉末床重新暴露在喷雾区域的速率的竞争，第2个发生在液滴完全渗透到粉末床的速率和被润湿的粉末床重新回到喷雾区域的速率之间，定义无尺度流量参数Ψa和无尺度液滴渗透时间τp来描述[25]。Litster等[26]基于无尺度参数Ψa和τp建立成核阶段的Regime Map示意图。如图1所示。在润湿和成核Regime Map中，根据Ψa和τp的大小划分了3个区域：液滴控制区、中间水平区以及机械分散区。当Ψa和τp值均较小时，润湿与成核发生在液滴控制区，每一滴粘合剂都可以形成一个颗粒核;随着Ψa和τp不断增大，进入中间水平区，由于液滴的聚集作用，颗粒核数量不断增加，颗粒核的粒径分布也随之增大;随着Ψa和τp进一步增大，进入机械分散区，颗粒核表面过强的聚集作用引起结块，需要机械外力来破碎这些团块。

图1 润湿与成核模式地图[24]

注：Ψa：无尺度流量，τp：无尺度渗透时间

2）成长与致密化Regime Map粉末通过聚集形成颗粒核后，进而聚合成长。颗粒成长的类型很大程度取决于颗粒在碰撞开始时具有的动能与碰撞过程中消耗能量的大小，为了函数化的描述这种竞争关系，定义最大颗粒孔隙饱和度Smax[27]和斯托克斯变形数Stdef[28]。當Smax大于1时，暗示着粘合剂不仅仅存在于颗粒的内部，也存在于颗粒的表面，这就增加大了颗粒之间黏连的可能性。同时在粒子相互碰撞的过程中，由于颗粒表面的粘合剂分布而增大了黏性损耗，造成结块。在将润湿与成核Regime Map控制在液滴可控区的前提下，Iveson等[26]建立颗粒成长阶段Regime Map示意图。如所示，颗粒成长分为3种方式：诱导成长、稳定成长和快速成长。当液体的量太少的时候，颗粒之间的聚集作用太小，只能形成颗粒核，而无法形成颗粒。当液体的量达到一定的水平，液体由于挤压附着在颗粒核表面形成液体层，液体层将周围的颗粒聚集在一起，即诱导成长。稳定成长的特点是颗粒与颗粒形成一个更大的接触面，颗粒稳定的长大，对原物料和工艺条件的更改的适应性强。当液体的量过多，颗粒呈快速成长方式，快速成长方式不容易控制，而且过多液体会形成药浆。

基于Regime Map的无尺度建模的方法可以加深对湿法制粒过程的理解，目前已有处方对润湿与成核Regime Map的实验验证，例如有机物体系微晶纤维素-去离子水[29]，α-乳糖-HPC[23-24，30-31]，以及无机物体系铜精矿-水[32]。对于成长与致密化Regime Map，Iveson定义出了各种成长模式的理论边界，并在挤出-滚圆制粒中得到了较好的验证[26]，但在高速剪切湿法制粒过程中的验证结果较差，可能的原因是由于对粒子相对碰撞速率以切割刀转速进行估计。而近期研究发现颗粒相对碰撞速率选取10%～20%的搅拌桨线速度进行估计，效果较好[33-34]，但仍未见Iveson利用这一结果进行原有数据的验证。与润湿与成核的Regime Map不同的是，近年来未见成长与致密化的Regime Map在高速剪切湿法制粒过程的直接验证。可能的原因是由于动态屈服应力的测量条件较为苛刻。

图2 成长模式地图[26]

注：Stdef：斯托克斯变形数，Smax：最大颗粒孔饱和度，ρg：颗粒密度，U：相对碰撞速率，Y：动态屈服强度，w：液固质量比，ρs：固体密度，ρl：液体密度，εmin：最小孔隙率

相比润湿与成核、成长与致密化阶段，对于磨损与破碎阶段的Regime Map研究非常少。Tardos等基于斯托克斯变形数Stdef，提出当Stdef超过某一极限值时，颗粒就会破碎[25]。该结论在成长与致密化Regime Map图上可以得到反映：成长与碎屑区的交界线（Stdef=0.02）可能是这个极限值。已有实验对该模型进行了验证，但颗粒强度的定义和Stdef极限值与原有Regime Map略微不同[35-36]。

1.3.2 基于Regime Map的HSWG过程放大理论 Regime Map中的无尺度参数较好的描述了颗粒润湿成核阶段、成长致密化阶段下的微环境，并且可以看出无尺度参数与工艺规模并无联系，表明Regime Map的无尺度参数不受工艺规模的限制，属于HSWG放大研究中的动态设计空间，可以用来指导放大研究。而HSWG过程工艺放大面临的问题主要有3个方面[37]：混合器几何构造、粉体流动模式、制粒速率过程。而无尺度模型能够较好的应对这3方面的问题。

1.3.2.1 混合器几何构造 高速剪切湿法制粒机集混合、制粒过程为一体，混合器是制粒机的关键部分。对于混合器的构造，关键规格尺寸主要有搅拌桨直径D，通常等于混合器底部圆面的直径，切割刀直径Dc，粉体填装高度Hm。混合器几何构造的相似性用无尺度参数表示为DcD，HmD，工艺放大后，无尺度参数应该保持不变。此外，搅拌桨和切割刀的位置和形状也应该保持一致。

1.3.2.2 粉体流动模式 粉体在制粒机中的流动摸式有沸腾旋转和牵拉旋转2种[39]，当搅拌桨的转速较低时，粉体呈现沸腾旋转，粉体沸腾旋转的区域称为沸腾旋转区;当搅拌桨的转速较高时，粉体呈现牵拉旋转，粉体牵拉旋转的区域成为牵拉旋转区。粉体流动由沸腾旋转变为牵拉旋转是因为离心力和重力平衡发生了改变，粉体转动惯量和重力的比值用弗劳德数（Froude Number，Fr）表示，即

其中N代表搅拌桨转速，g代表粉体的重力加速度。

通常，当Fr高于临界值（Frc），粉体就会由沸腾旋转变为牵拉旋转。Frc的大小与相对填充高度（N2N1=D1D2）、搅拌桨的形状和规格以及粉体流动性能有关。

在沸腾旋转区，粉体表面速度随着搅拌桨转速的增大而增大，在牵拉旋转区，粉体表面速度比较稳定，受搅拌桨转速的影响很小。粉体表面速度只有搅拌桨外缘速度的10%，Knight等[31]发现无尺度力矩T是关于Fr和有效叶片高度heff的函数：

在放大过程中为了维持相似的粉体流动模式，不同生产规模的Fr应该保持不变，即N2N1=D1D2。此外，相对填充高度也应该保持不变，即Hm，2Hm，1=D2D1。

高速剪切制粒机设备通常是以恒定的外缘速率进行放大的，这种放大方式就会导致Fr的降低，而且还会导致粉体牵拉旋转变为沸腾旋转。考虑到高速剪切湿法制粒机工艺放大后几何构造的变化，还可以考虑以恒定相对波及体积的方法进行放大。相对波及体积（VR）的表达式如下：

其中Vimp表示攪拌桨波及体积的速率，Vmixer表示混合器的体积。

1.3.2.3 制粒速率过程 高速剪切湿法制粒的速率过程对粒径分布都有显著的影响。润湿和成核阶段，在液滴可控区，粉末可以形成良好颗粒核，这就需要将Ψa控制在较低的范围内。为了维持相似的颗粒核形成方式，即颗粒成核内环境，工艺放大后Ψa应保持不变。假设液滴直径不变，工艺放大后需满足：

通常采用的放大方法是保持相同的总液体喷洒时间和使用同型号的喷嘴。然而这样，随着D3成比例增大，尽管随着工艺放大也会微微增大，但是这种方法通常会导致Ψa大幅度增大。为了保持Ψa不变，放大后的工艺就需要使用多个喷嘴和延长液体喷洒的时间[39]。

颗粒成长阶段速率过程比较复杂，该过程包含了复杂的颗粒成长方式，不同成长方式取决于Smax和Stdef。为了保持工艺放大后颗粒的成长方式不变，Smax和Stdef应保持不变。对于，Smax，需要保持液固质量比不变。对于Stdef，在高速剪切湿法制粒机中，最大碰撞速度取决于搅拌桨外缘速度，那么Stdef不变意味着搅拌桨外缘速度不变，即需要满足

因此，生产工艺扩大，Stdef也随之增大。这样就会导致最大可实现颗粒密度的增大和最大可实现粒径的降低。实际过程中，颗粒密度和粒径还取决于成长和致密化的动力学过程，因此没有更为可靠的定量模型，颗粒在成长速率过程很难预测。高速剪切湿法制粒过程复杂，采用一般方法建立的模型，在工艺放大后往往并不适用。根据无尺度参数建立Regime Map进行工艺放大的关键就是保持无尺度参数恒定，从而能够预测放大后工艺参数的变动，控制工艺放大后产品的质量。

1.3.3 基于Regime Map的HSWG过程放大研究实例

本部分选取了以润湿与成核Regime Map指导HSWG过程放大的1个案例。该案例以微晶纤维素（MCC）-水作为研究载体，以润湿与成核Regime Map作为指导，以1 L工艺规模的颗粒作为基准，对比2 L、4 L工艺规模下所得颗粒的产率、颗粒粒径概率分布曲线及其相似度、扫描电镜（SEM）图，以及对比其基于SeDeM方法建立的物理指纹图谱，成功实现了在SHK-4型高速剪切湿法制粒机从1 L到2 L、4 L的放大[40]。

1.3.3.1 工艺参数设置 SHK-4型高速剪切湿法制粒机是锅体可替换型制粒机，1 L、2 L和4 L制粒锅的几何参数如表3所示。基于前期小试HSWG的研究[27]，HSWG在1 L的工艺规模下所得的关键工艺参数是水用量和湿混时间，那么以水用量和湿混时间作为均匀设计的2个参数进行U5（52）均匀设计进行放大研究，实验点安排如表4所示。

表3 SHK-4型高速剪切湿法制粒机

3个制粒锅的几何参数

表4 U5（52）均匀设计实验安排表

由于3工艺规模下均使用同样的蠕动泵，假设水的颗粒大小保持不变，根据1.3.3.2项下计算：为保证两工艺规模下无尺度流量参数保持一致，则需

那么则可推导出：

其中下标1，2分别代表工艺规模1和工艺规模2，t是水加入制粒锅的时间，V是水加入的总量，r是搅拌桨的半径。而1 L、2 L和4 L规模所用MCC分别为100 g、200 g和400 g，水加入时间分别为300 s、442 s和700 s，每个工艺规模下5个实验点蠕动泵的转速如表5所示。

表5 MCC颗粒在1 L、2 L和4 L规模下蠕动泵的转速

1.3.3.3 颗粒评价结果 以1 L工艺规模下所得颗粒作为基准，对比2 L和4 L规模下所得颗粒的颗粒得率、粒径概率分布曲线及相似度[41]、SEM图、基于SeDeM的物理指纹图谱[42-46]，分别见表6、图3和表7、图4以及图5。

表6 3工艺规模下颗粒得率（%）

图3 3工艺规模下颗粒粒径概率分布曲线

表7 以1 L规模下颗粒为基准，2 L和4 L规模

所得颗粒粒径分布曲线的相似度

图4 实验点1所得颗粒在3工艺规模下，

3放大倍数下的SEM图

注：其中a，b，c分别代表1 L、2 L和4 L，h，m，l分别代表放大倍数为10 000倍，5 000倍和2 000倍

图5 15批MCC颗粒的SeDeM物理指纹图谱

注：其中Db、Dt、Ie、IC、IH、α、t′′、%RH、%H、%Pf、Iθ分别代表松装密度、振实密度、颗粒间空隙率、卡尔指数、豪斯纳比率、休止角、粉末流动时间、干燥失重、吸湿性、粒径小于50 μm百分比和相对均齐度指数

收率结果显示几乎所有批次的颗粒均大于85%，且对于同一实验点，1 L、2 L和4 L 3工艺规模所得颗粒的收率一致。所有颗粒的向量夹角余弦法计算结果均大于0.9，表明与小试颗粒相比放大所得颗粒的粒径概率分布曲线相似度高，放大所得颗粒与小试颗粒具有较好的质量相似性。由SEM图可见在3个放大倍数下，MCC颗粒具有相似的表面形态。SeDeM物理指纹图谱也可以看出，对于同一实验点，放大所得颗粒与小试颗粒具有较好的质量相似性，暗示着放大成功。

2 讨论

本文介绍了质量源于设计在中药制药过程放大研究中的应用，列举了常用的放大研究方法，详细介绍了数学模拟放大，即基于模型的放大，并实例分析了以润湿成核阶段的模式地图指导放大高速剪切湿法制粒过程的研究。保持无尺度参数在放大过程中的恒定，或构建出工艺规模变化时相对稳定的动态设计空间，能够得到较为理想的放大结果。但由于描述过程机理的无尺度参数开发具有一定的难度，所以目前开发出的类似模式地图的动态设计空间的过程仅是高速剪切湿法制粒过程，无尺度建模的理论在其他过程的应用需要进一步的研究。

参考文献

[1]徐冰，史新元，吴志生，等.论中药质量源于设计[J].中国中药杂志，2017，42（6）：1015-1024.

[2]M Zlokarnik.Dimensional Analysis and Scale-Up in Chemical Engineering[M].New York：Springer-Verlag，1991.

[3]徐冰，史新元，乔延江，等.中药制剂生产工艺设计空间的建立[J].中国中药杂志，2013，38（6）：924-929.

[4]Iveson SM，Litster JD，Hapgood K，et al.Nucleation，growth and breakage phenomena in agitated wet granulation processes：a review[J].Powder Technology，2001，117（1-2）：3-39.

[5]Kapur PC，Fuerstenau DW.Size distributions and kinetic relationships in nuclei region of wet pelletization[J].Industrial and Engineering Chemistry Process Design and Development，1966，5（1）：5-10.

[6]Austin LG.Introduction to the mathematical description of grinding as a rate process[J].Powder Technology，1971，5（5）：1-17.

[7]KVS Sastry，Fuerstenau DW.Kinetics of green pellet growth by the layering mechanism[J].Transactions of the American Institute of Mining and Metallurgical Engineers，1977（262）：43-47.

[8]Litster JD，Waters AG，Nicol SK.A model for predicting the size distribution of product from a granulating drum[J].Transactions of the Iron and Steel Institute of Japan，2006，26（12）：1036-1044.

[9]M.J.Hounslow，R.L.Ryall，V.R.Marshall.A discretized population balance for nucleation，growth，and aggregation[J].Aiche Journal，1988，34（11）：1821-1832.

[10]Detayo AA A，Litster JD，Pratsinis SE，et al.Population balance modelling of drum granulation of materials with wide size distribution[J].Powder Technology，1995，82（1）：37-49.

[11]Verkoeijen D，Pouw GA，Meesters GMH，et al.Meesters，Brian Scarlett.Population balances for particulate processes—a volume approach[J].Chemical Engineering Science，2002，57（12）：2287-2303.

[12]Iveson SM.Limitations of one-dimensional population balance models of wet granulation processes[J].Powder Technology，2002，124（3）：219-229.

[13]Ingram GD，Cameron IT，Hangos KM.Classification and analysis of integrating frameworks in multiscale modeling[J].Chemical Engineering Science，2004，59（11）：2171-2187.

[14]楊洋，唐寿高.颗粒流的离散元法模拟及其进展[J].中国粉体技术，2006，12（5）：38-43.

[15]Pordal HS，Matice CJ，Fry TJ.The Role of Computational Fluid Dynamics in the Pharmaceutical Industry[J].Pharmaceutical Technology North America，2002，14（2）：1036.

[16]Terrazas-Velarde K，Peglow M，Tsotsas E.Stochastic simulation of agglomerate formation in fluidized bed spray drying：a micro-scale approach[J].Chemical Engineering Science，2009，64（11）：2631-2643.

[17]Link JM，Godlieb W，Tripp P，et al.Comparison of fibre optical measurements and discrete element simulations for the study of granulation in a spout fluidized bed[J].Powder Technology，2009，189（2）：202-217.

[18]Terrazas-Velarde K，Peglow M，Tsotsas E.Kinetics of fluidized bed spray agglomeration for compact and porous particles[J].Chemical Engineering Science，2011，66（9）：1866-1878.

[19]Chua KW，Makkawi YT，Hounslow MJ.Hounslow，Time scale analysis for fluidized bed melt granulation I：granule-granule and granule-droplet collision rates[J].Chemical Engineering Science，2011，66（3）：318-326.

[20]Fries L，Antonyuk S，Heinrich S，et al.DEM-CFD modeling of a fluidized bed spray granulator[J].Chemical Engineering Science，2011，66（11）：2340-2355.

[21]Li Z，Kind M，Gruenewald G.Modeling the Growth Kinetics of Fluidized-Bed Spray Granulation[J].Chemical Engineering & Technology，2011，34（7）：1067-1075.

[22]Gantt JA，Gatzke EP.High-shear granulation modeling using a discrete element simulation approach[J].Powder Technology，2005，156（2-3）：195-212.

[23]Terashita K，Nishimura T，Natsuyama S.Optimization of operating conditions in a high-shear mixer using DEM model：determination of optimal fill level[J].Chemical & Pharmaceutical Bulletin，2002，50（12）：1550-1557.

[24]Bjrn IN，Jansson A，Karlsson M et al.Empirical tomechanistic modelling in high shear granulation[J].Chemical Engineering Science，2005，60（14）：3795-3803.

[25]Litster JD，Hapgood KP，Michaels JN，et al.Liquid distribution in wet granulation dimensionless spray flux[J].Powder Technology，2001，114（1）：32-39.

[26]Hapgood KP，Litster JD，Smith R.Nucleation regime map for liquid bound granules[J].Aiche Journal，2010，49（2）：350-361.

[27]Tardos GI，Khan MI，Mort PR.Critical parameters and limiting conditions in binder granulation of fine powders[J].Powder Technology，1997，94（3）：245-258.

[28]Iveson SM，Wauters PAL，Forrest S，et al.Growth regime map for liquid-bound granules：further development and experimental validation[J].Powder Technology，2001，117（1-2）：83-97.

[29]羅赣，徐冰，孙飞，等.基于QbD理念的微晶纤维素高速剪切湿法制粒过程实验研究[J].药学学报，2015，50（3）：355-359.

[30]Litster JD，Hapgood KP，Michaels JN，et al.Scale-up of mixer granulators for effective liquid distribution[J].Powder Technology，2002，124（3）：272-280.

[31]Ax K，Feise H，Sochon R，et al.Influence of liquid binder dispersion on agglomeration in an intensive mixer[J].Powder Technology，2008，179（3）：190-194.

[32]Wauters PAL，Jakobsen RB，Litster JD.Liquid distribution as a means to describing the granule growth mechanism[J].Powder Technology，2002，123（2-3）：166-177.

[33]Knight PC，Seville JPK，Wellm AB，et al.Prediction of impeller torque in high shear powder mixers[J].Chemical Engineering Science，2001，56（15）：4457-4471.

[34]A.Tran.Powder flow properties in vertical high shear mixers[D].Australia：University of Queensland PhD Thesis，2007.

[35]Dries KVD，Vegt OMD，Girard V，et al.Granule breakage phenomena in a high shear mixer;influence of process and formulation variables and consequences on granule homogeneity[J].Powder Technology，2003，133（1-3）：228-236.

[36]Liu LX，Smith R，Litster JD.Wet granule breakage in a breakage only high-hear mixer：effect of formulation properties on breakage behavior[J].Powder Technology，2009，189（2）：158-164.

[37]Y He，LX Liu，JD Litster.Handbook of Pharmaceutical Granulation Technology Chapter 25：Scale-Up Considerations in Granulation[M].New York：Informa Healthcare，2009：538-566.

[38]Litster J.Forward to special edition of powder technology from “Control of Particulate Processes VI”[J].Powder Technology，2002，124（3）：175.

[39]Kayrak-Talay D，Dale S，Wassgren C.Quality by design for wet granulation in pharmaceutical processing：Assessing models for a priori design and scaling[J].Powder Technology，2013，240（5）：7-18.

[40]Luo G，Xu B，Zhang Y，et al.Scale-up of a high shear wet granulation process using a nucleationregime map approach[J].Particuology，2017，31（2）：87-94.

[41]王龙星，肖红斌，梁鑫淼，等.一种评价中药色谱指纹谱相似性的新方法：向量夹角法[J].药学学报，2002，37（9）：713-717.

[42]Aguilar-Díaz JE，García-Montoya E，P Pérez-Lozano，et al.The use of the SeDeM Diagram expert system to determine the suitability of diluents-disintegrants for direct compression and their use in formulation of ODT[J].European Journal of Pharmaceutics and Biopharmaceutics，2009，73（3）：414-423.

[43]Aguilar-Díaz JE，García-Montoya E，Pérez-Lozano P.SeDeM expert system a new innovator tool to develop pharmaceutical forms[J].Drug Development and Industrial Pharmacy，2014，40（2）：222-236.

[44]Negre JMS，Montoya EG，Lozano PP，et al.SeDeM diagram：A new expert system for the formulation of drugs in solid form[M].The Philippines：InTech，2011.

[45]Pérez P，Sué-Negre JM，Miarro M，et al.A new expert systems （SeDeM Diagram） for control batch powder formulation and preformulation drug products[J].European Journal of Pharmaceutics and Biopharmaceutics，2006，64（3）：351-359.

[46]張毅，徐冰，孙飞，等.中药提取物粉末物理指纹谱研究及应用[J].中国中药杂志，2016，41（12）：2221-2227.